標準化されたテスト統計とは何ですか?
統計的仮説は、 母集団パラメータに関する仮定です。たとえば、米国の男性の平均身長が 70 インチであると仮定できます。身長に関する仮説は統計的仮説であり、米国男性の真の平均身長が母集団パラメータです。
仮説検定は、統計的仮説を棄却または棄却できなかったために使用する正式な統計検定です。
仮説検定を実行する基本的なプロセスは次のとおりです。
1.サンプルデータを収集します。
2.サンプルデータの標準化された検定統計量を計算します。
3.標準化されたテスト統計量を臨界値と比較します。臨界値より極端な場合は、帰無仮説を棄却します。それ以外の場合は、帰無仮説検定を拒否しないでください。
標準化された検定統計量を計算するために使用する式は、実行する仮説検定の種類によって異なります。
次の表は、仮説検定の 4 つの主なタイプごとに標準化された検定統計量を計算するために使用する式を示しています。
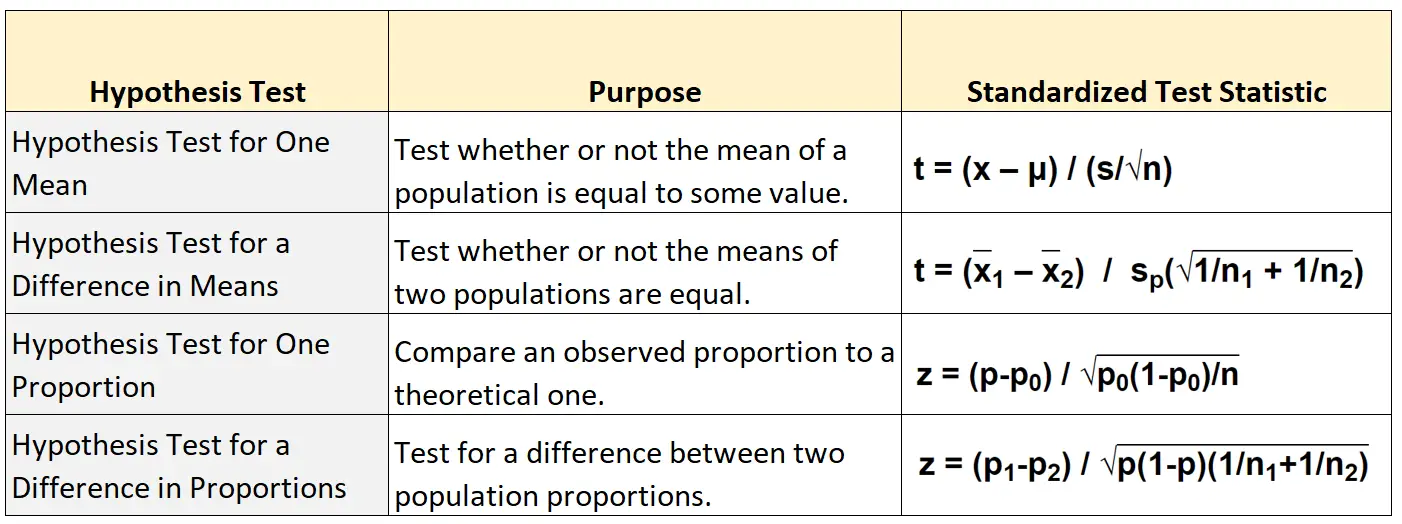
平均値の仮説検定
1 サンプル t 検定は、母集団の平均が特定の値に等しいかどうかを検定するために使用されます。
このタイプのテストの標準化されたテスト統計は次のように計算されます。
t = ( X – μ) / (s/√n)
金:
- x:サンプルの平均値
- μ 0 :仮説上の母集団平均
- s:サンプルの標準偏差
- n:サンプルサイズ
この標準化されたテスト統計量を計算する例については、 このチュートリアルを参照してください。
平均値の違いに関する仮説検定
2 標本 t 検定は、 2 つの母集団の平均が等しいかどうかを検定するために使用されます。
このタイプのテストの標準化されたテスト統計は次のように計算されます。
t = ( X 1 – X 2 ) / s p (√ 1/n 1 + 1/n 2 )
ここで、x 1と x 2はサンプル平均、n 1と n 2はサンプルサイズ、s p は次のように計算されます。
s p = √ (n 1 -1)s 1 2 + (n 2 -1)s 2 2 / (n 1 +n 2 -2)
ここで、s 1 2と s 2 2は標本分散です。
この標準化されたテスト統計量を計算する例については、 このチュートリアルを参照してください。
割合の仮説検定
1 比率 Z 検定は、観測された比率を理論上の比率と比較するために使用されます。
このタイプのテストの標準化されたテスト統計は次のように計算されます。
z = (pp 0 ) / √ p 0 (1-p 0 )/n
金:
- p:観測されたサンプルの割合
- p 0 :人口の仮説的な割合
- n:サンプルサイズ
この標準化されたテスト統計量を計算する例については、このチュートリアルを参照してください。
比率の違いに関する仮説検定
2 つの比率の Z 検定は、 2 つの母集団比率の差を検定するために使用されます。
このタイプのテストの標準化されたテスト統計は次のように計算されます。
z = (p 1 -p 2 ) / √ p(1-p)(1/n 1 +1/n 2 )
ここで、p 1と p 2はサンプルの割合、n 1と n 2はサンプル サイズ、p は次のように計算されたプールされた合計の割合です。
p = (p 1 n 1 + p 2 n 2 )/(n 1 + n 2 )
この標準化されたテスト統計量を計算する例については、 このチュートリアルを参照してください。