機械学習における過学習とは何ですか? (説明と例)

機械学習では、特定の現象について正確に予測できるようにモデルを構築することがよくあります。

たとえば、予測変数の勉強に費やした時間を使用して、高校生の応答変数のACT スコアを予測する回帰モデルを作成するとします。

このモデルを構築するために、特定の学区の数百人の生徒の学習時間とそれに対応する ACT スコアに関するデータを収集します。

次に、このデータを使用して、総学習時間数に基づいて特定の生徒が受け取るスコアを予測できるモデルをトレーニングします。

モデルの有用性を評価するには、モデルの予測が観察されたデータとどの程度一致するかを測定できます。これを行うために最も一般的に使用される指標の 1 つは平均二乗誤差 (MSE) で、次のように計算されます。

MSE = (1/n)*Σ(y _i – f(x _i )) ²

金：

• n:観測値の総数
• y _i : ^{i 番目}の観測値の応答値
• f( _xi ): i^番目の観測値の予測応答値

モデルの予測が観測値に近づくほど、MSE は低くなります。

ただし、機械学習で犯される最大の間違いの 1 つは、トレーニング MSE (モデルの予測がモデルのトレーニングに使用したデータとどの程度一致するか) を減らすためにモデルを最適化することです。

モデルがトレーニング MSE の削減に重点を置きすぎると、単に偶然によって引き起こされたトレーニング データ内のパターンを見つけることが難しくなることがよくあります。そして、そのモデルを目に見えないデータに適用すると、そのパフォーマンスは低下します。

この現象は、オーバーフィッティングとして知られています。これは、モデルをトレーニング データに近づけすぎて、新しいデータの予測に役に立たないモデルを構築してしまう場合に発生します。

過学習の例

過学習を理解するために、 ACT スコアを予測するために費やした学習時間を使用する回帰モデルを作成する例に戻りましょう。

特定の学区の 100 人の生徒のデータを収集し、2 つの変数間の関係を視覚化する簡単な散布図を作成するとします。

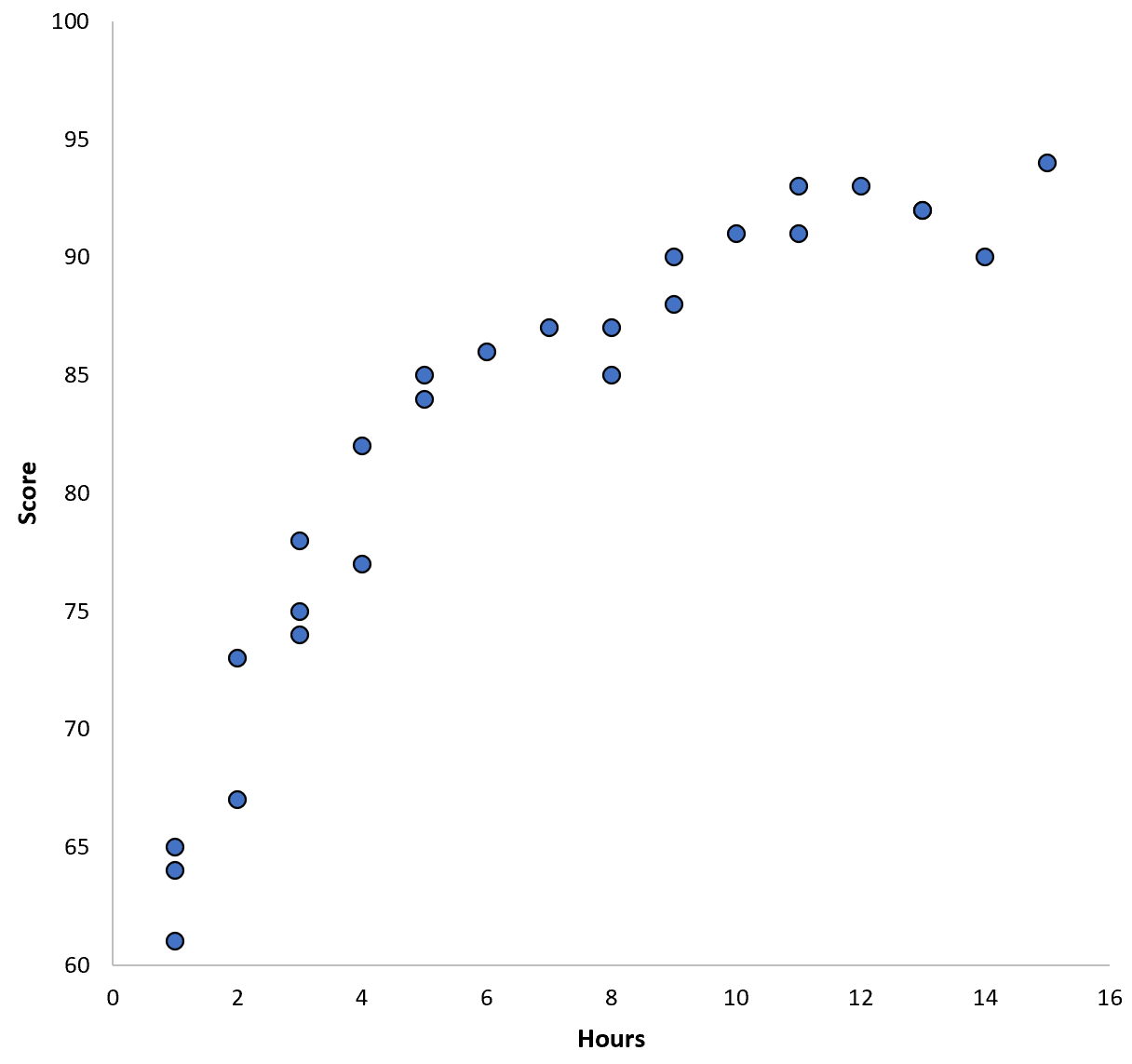
2 つの変数間の関係は 2 次であるように見えるため、次の 2 次回帰モデルを適用するとします。

スコア = 60.1 + 5.4*(時間) – 0.2*(時間) ²

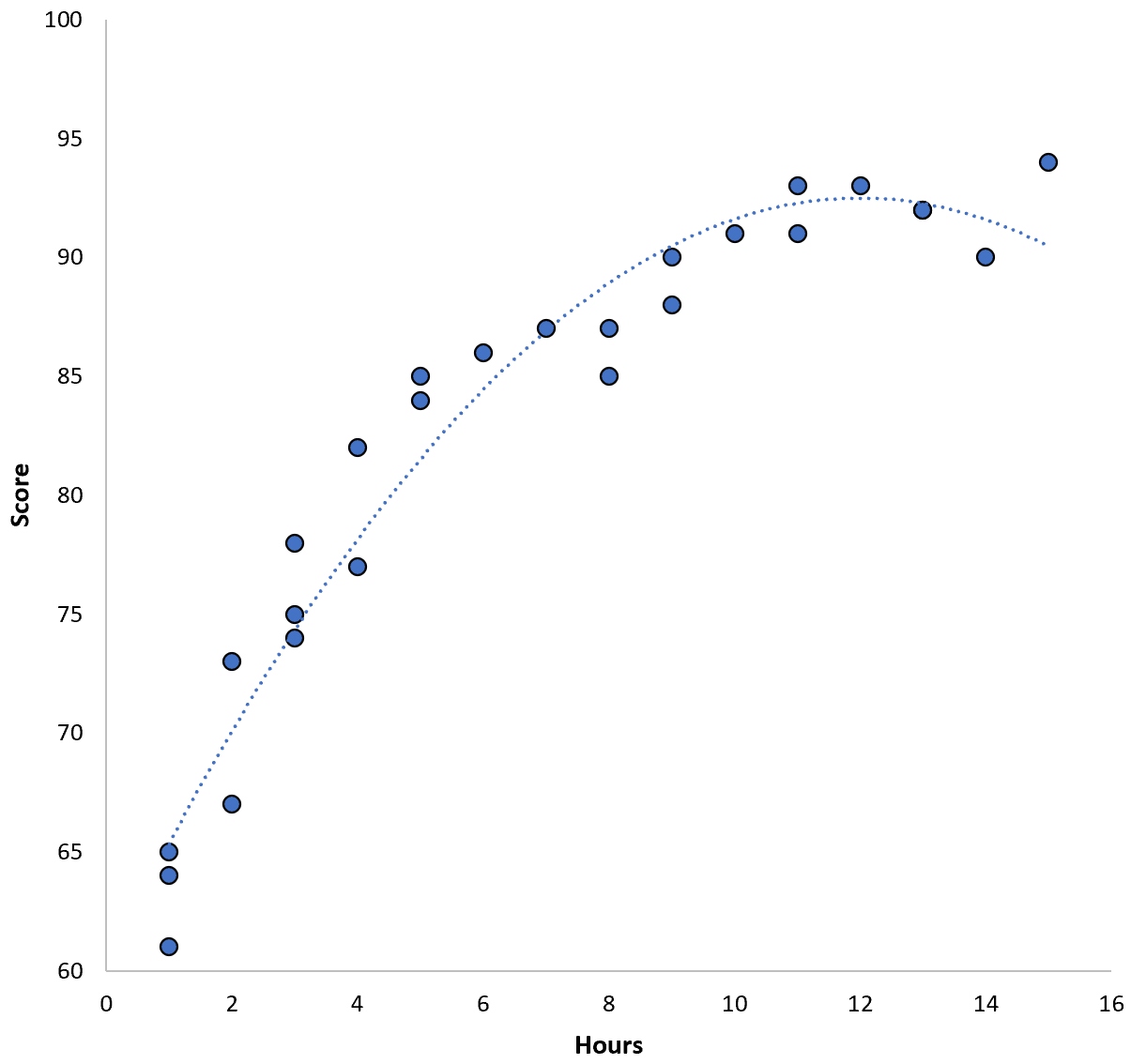
このモデルのトレーニング平均二乗誤差 (MSE) は3.45です。つまり、モデルによって行われた予測と実際の ACT スコアの間の二乗平均平方根の差は 3.45 です。

ただし、高次の多項式モデルをフィッティングすることで、このトレーニング MSE を減らすことができます。たとえば、次のモデルを適用するとします。

スコア = 64.3 – 7.1*(時間) + 8.1*(時間) ² – 2.1*(時間) ³ + 0.2*(時間^{) 4 – 0.1*(時間) 5 +} 0.2(時間) ⁶

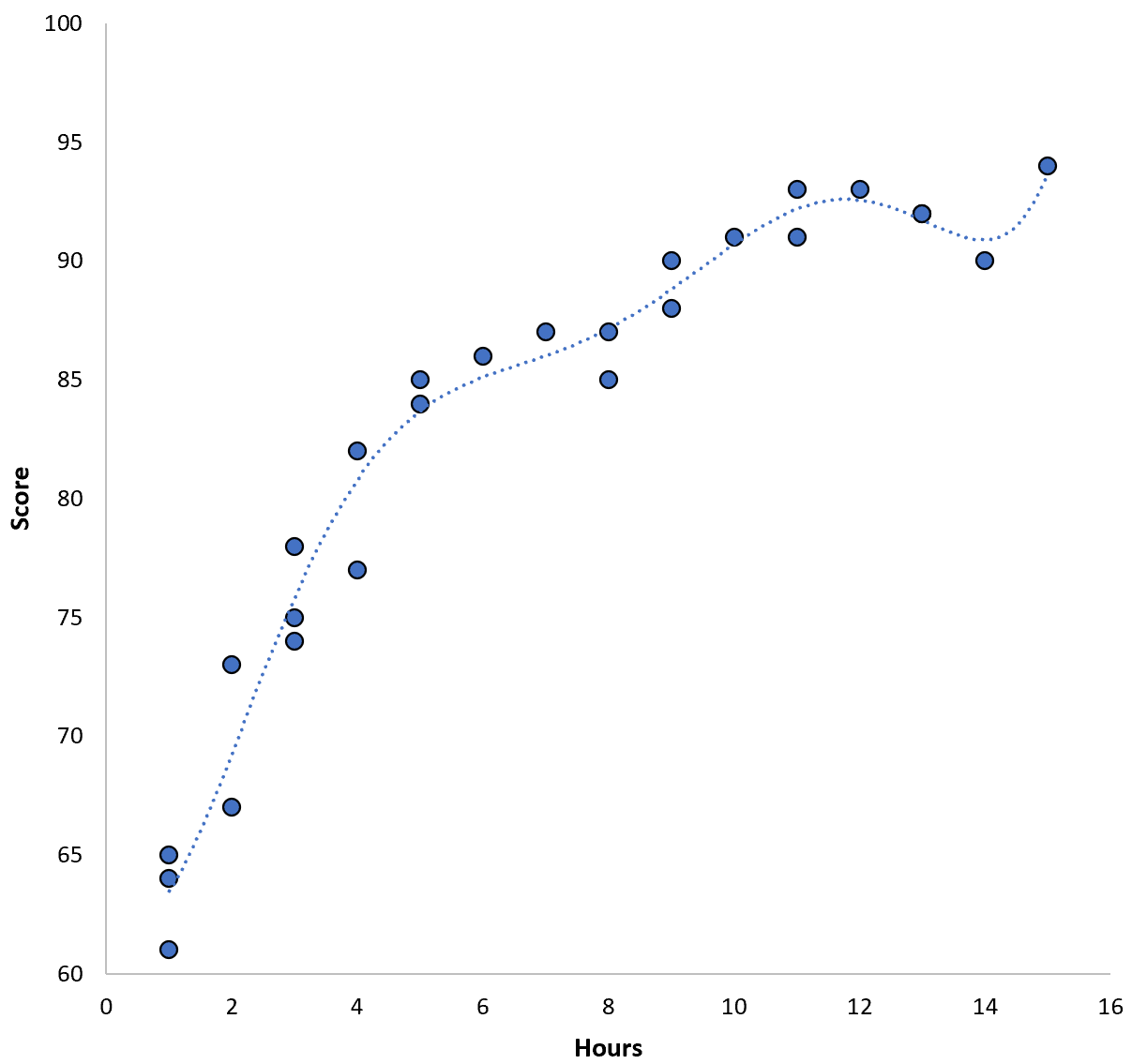
回帰直線が前の回帰直線よりも実際のデータにかなり近似していることに注目してください。

このモデルのトレーニング二乗平均平方根誤差 (MSE) はわずか0.89です。つまり、モデルによって行われた予測と実際の ACT スコアの間の二乗平均平方根の差は 0.89 です。

この MSE トレーニングは、以前のモデルによって生成されたものよりもはるかに小さいです。

ただし、トレーニング MSE 、つまりモデルの予測がモデルのトレーニングに使用したデータとどの程度一致するかについてはあまり気にしません。代わりに、私たちは主にMSE テスト、つまりモデルが目に見えないデータに適用されるときの MSE に注目します。

上記の高次多項式回帰モデルを目に見えないデータセットに適用した場合、単純な 2 次回帰モデルよりもパフォーマンスが低下する可能性があります。つまり、より高い MSE テストが生成されることになりますが、これはまさに望ましくないことです。

過学習を検出して回避する方法

過学習を検出する最も簡単な方法は、相互検証を実行することです。最も一般的に使用される方法はk 分割交差検証として知られており、次のように機能します。

ステップ 1: データセットを、ほぼ同じサイズのk個のグループ、つまり「分割」にランダムに分割します。

ステップ 2: 保持セットとしてフォールドの 1 つを選択します。テンプレートを残りの k-1 個の折り目に合わせて調整します。張力がかかった層の観察結果に基づいて MSE テストを計算します。

ステップ 3: 毎回異なるセットを除外セットとして使用して、このプロセスをk回繰り返します。

ステップ 4: テストの全体的な MSE を、テストのk個の MSE の平均として計算します。

テスト MSE = (1/k)*ΣMSE _i

金：

• k:折り数
• MSE _i : ⁱ回目の反復で MSE をテストします

この MSE テストにより、特定のモデルが未知のデータに対してどのように動作するかについての良いアイデアが得られます。

実際には、いくつかの異なるモデルを当てはめ、各モデルに対して k 分割交差検証を実行して、その MSE テストを見つけることができます。その後、MSE テストが最も低いモデルを、将来の予測に使用する最適なモデルとして選択できます。

これにより、単にトレーニング MSE を最小限に抑えて過去のデータによく「適合」するモデルではなく、将来のデータで最高のパフォーマンスを発揮する可能性が高いモデルを確実に選択できます。

追加リソース

機械学習におけるバイアスと分散のトレードオフとは何ですか?
K-Fold 相互検証の概要
機械学習における回帰モデルと分類モデル