Ti-84 電卓で正規確率を計算する方法
正規分布は、すべての統計で最も一般的に使用される分布です。このチュートリアルでは、TI-84 計算機で次の関数を使用して正規分布確率を見つける方法を説明します。
Normalpdf(x, μ, σ) は、正規確率密度関数に関連付けられた確率を返します。ここで、
- x = 個体値
- μ = 母平均
- σ = 母標準偏差
Normalcdf( lower_x, upper_x, μ, σ) は、 2 つの値の間の正規 cdf に関連付けられた累積確率を返します。
金:
- lower_x = より低い個体値
- upper_x = 上限個体値
- μ = 母平均
- σ = 母標準偏差
これら 2 つの関数には、TI-84 電卓で2nd を押してからvarsを押すとアクセスできます。これにより、 DISTR画面が表示され、そこでNormalpdf()とNormalcdf()を使用できるようになります。
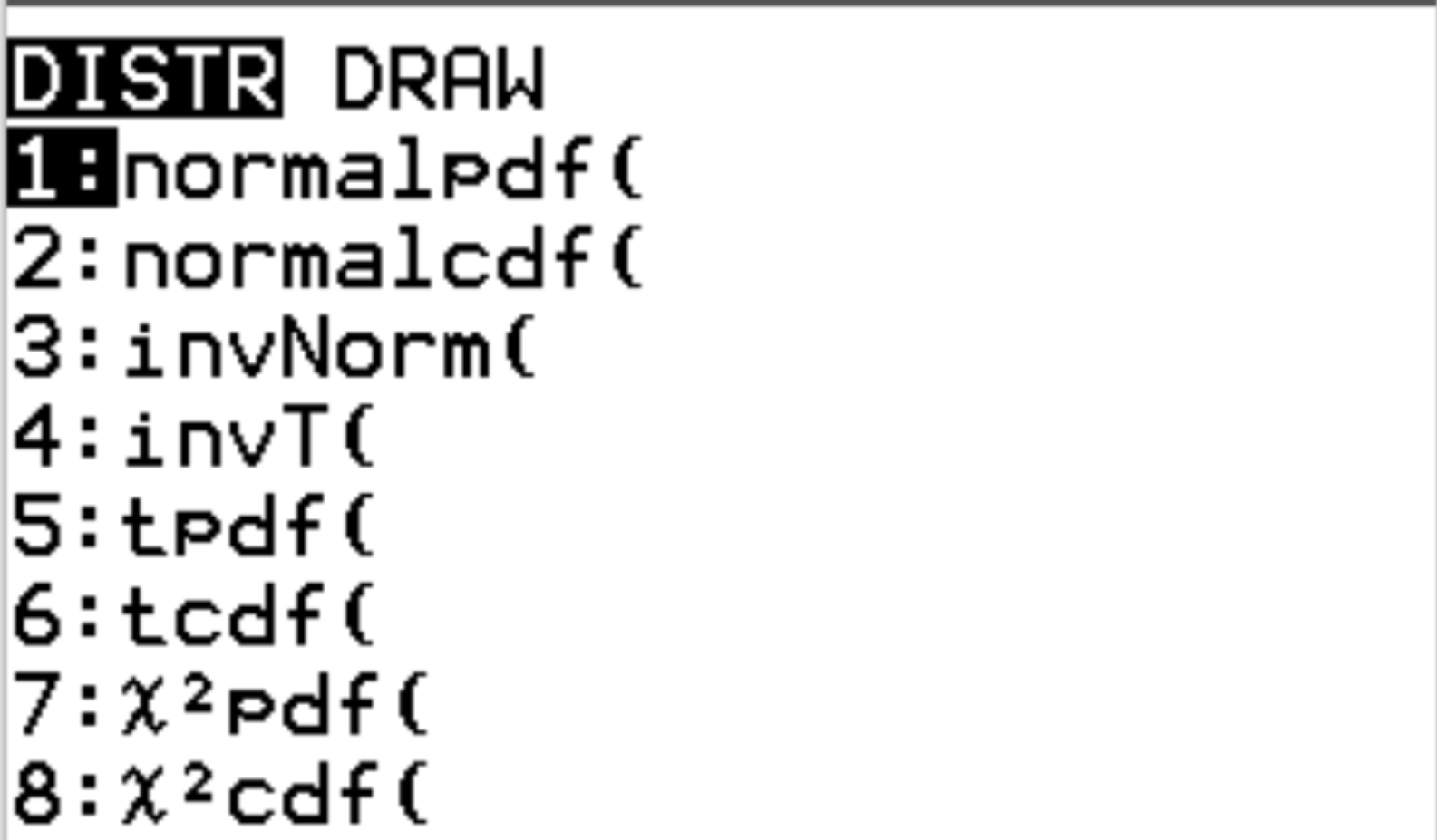
次の例は、これらの関数を使用してさまざまな質問に答える方法を示しています。
例 1: x より大きい正規確率
質問:平均 = 40、標準偏差 = 6 の正規分布について、値が 45 より大きくなる確率を求めます。
答え: Normalcdf(x, 10000, μ, σ) 関数を使用します。
Normalcdf(45, 10000, 40, 6) = 0.2023
注: この関数には upper_x 値が必要なので、単純に 10,000 を使用します。
例 2: x 未満の正規確率
質問:平均 = 100、標準偏差 = 11.3 の正規分布について、値が 98 未満になる確率を求めます。
答え: Normalcdf(-10000, x, μ, σ) 関数を使用します。
Normalcdf(-10000, 98, 100, 11.3) = 0.4298
注: この関数には lower_x 値が必要なので、単純に -10000 を使用します。
例 3: 2 つの値間の正規確率
質問:平均 = 50、標準偏差 = 4 の正規分布について、値が 48 ~ 52 の間にある確率を求めます。
答え: Normalcdf(smaller_x, Larger_x, μ, σ) 関数を使用します。
Normalcdf(48, 52, 50, 4) = 0.3829
例 4: 2 つの値を除いた正規確率
質問:平均 = 22、標準偏差 = 4 の正規分布について、値が 20 未満であるか、または 24 より大きい確率を求めます。
答え:関数normalcdf(-10000, small_x, μ, σ) + Normalcdf(larger_x, 10000, μ, σ)を使用します。
Normalcdf(-10000, 20, 22, 4) + Normalcdf(24, 10000, 22, 4) = 0.6171