統計における残差とは何ですか?
残差とは、回帰分析における観測値と予測値の差です。
次のように計算されます。
残差 = 観測値 – 予測値
線形回帰の目的は、1 つ以上の予測変数と応答変数の間の関係を定量化することであることを思い出してください。これを行うために、線形回帰は、最小二乗回帰直線と呼ばれる、データに最もよく「適合」する直線を見つけます。
この直線はデータセット内の各観測値の予測を生成しますが、回帰直線によって行われた予測が観測値と正確に一致する可能性はほとんどありません。
予測と観測値の差が残差です。観測値をプロットし、近似された回帰直線を重ね合わせると、各観測値の残差は観測値と回帰直線の間の垂直距離になります。

観測値が回帰直線によって作成された予測値よりも大きい場合、観測値は正の残差となります。
逆に、観測値が回帰直線によって作成された予測値よりも小さい場合、その観測値は負の残差となります。
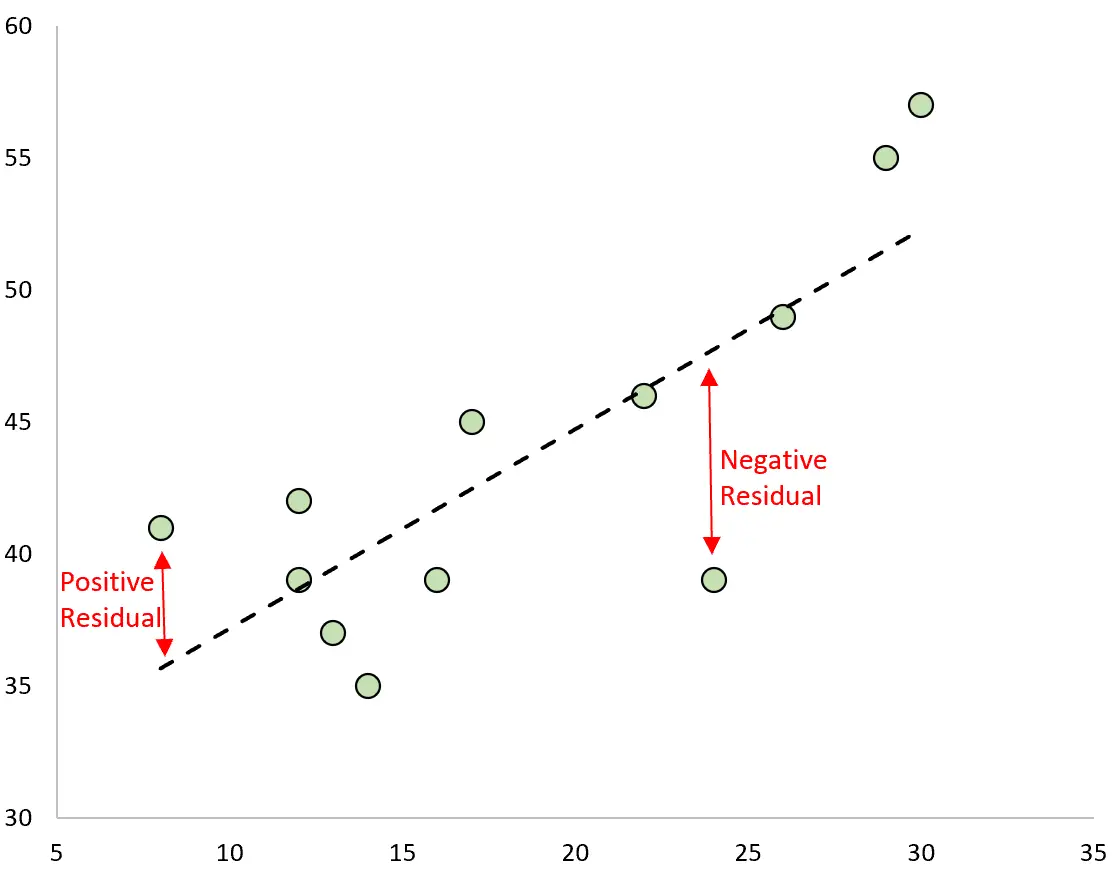
一部の観測値は正の残差を持ち、他の観測値は負の残差を持ちますが、すべての残差の合計は0 になります。
残差の計算例
合計 12 個の観測値を含む次のデータセットがあるとします。

統計ソフトウェア ( R 、 Excel 、 Python 、 Stataなど) を使用して線形回帰直線をこのデータセットに近似すると、最適な直線は次のようになります。
y = 29.63 + 0.7553x
この線を使用すると、X の値に基づいて各 Y 値の予測値を計算できます。たとえば、最初の観測値の予測値は次のようになります。
y = 29.63 + 0.7553*(8) = 35.67
この観測値の残差を次のように計算できます。
残差 = 実測値 – 予測値 = 41 – 35.67 = 5.33
このプロセスを繰り返して、各観測値の残差を見つけることができます。

散布図を作成して近似回帰直線を使用して観測値を視覚化すると、一部の観測値は線より上にあり、他の観測値は線より下にあることがわかります。
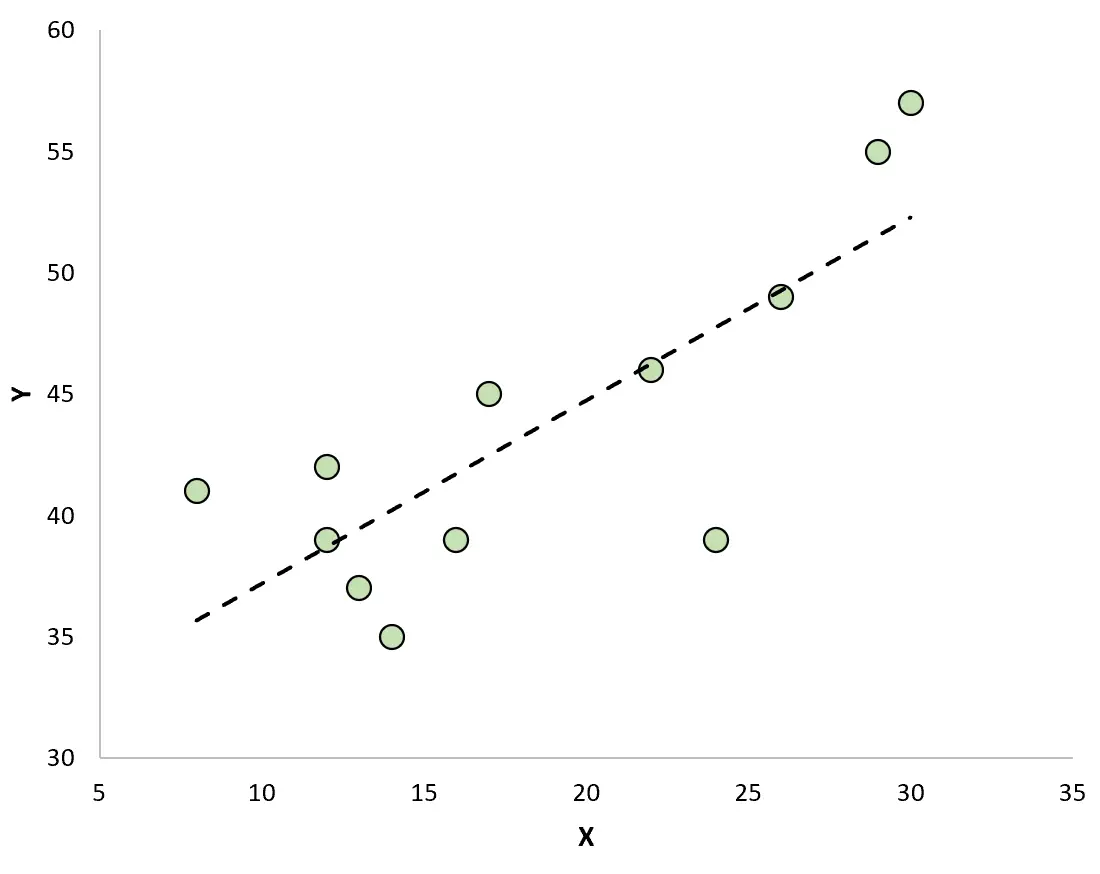
残基の性質
残基には次の特性があります。
- データセット内の各観測値には、対応する残差があります。したがって、データセットに合計 100 個の観測値が含まれている場合、モデルは 100 個の予測値を生成し、合計 100 個の残差が生成されます。
- すべての残差の合計はゼロです。
- 残差の平均値はゼロです。
残基は実際にどのように使用されますか?
実際には、回帰では残差が 3 つの異なる理由で使用されます。
1. モデルの適切性を評価します。
適合回帰直線を作成したら、すべての二乗残差の合計である残差二乗和 (RSS)を計算できます。 RSS が低いほど、回帰モデルはデータによく適合します。
2. 正規性の仮定を確認します。
線形回帰の重要な前提の 1 つは、残差が正規分布するということです。
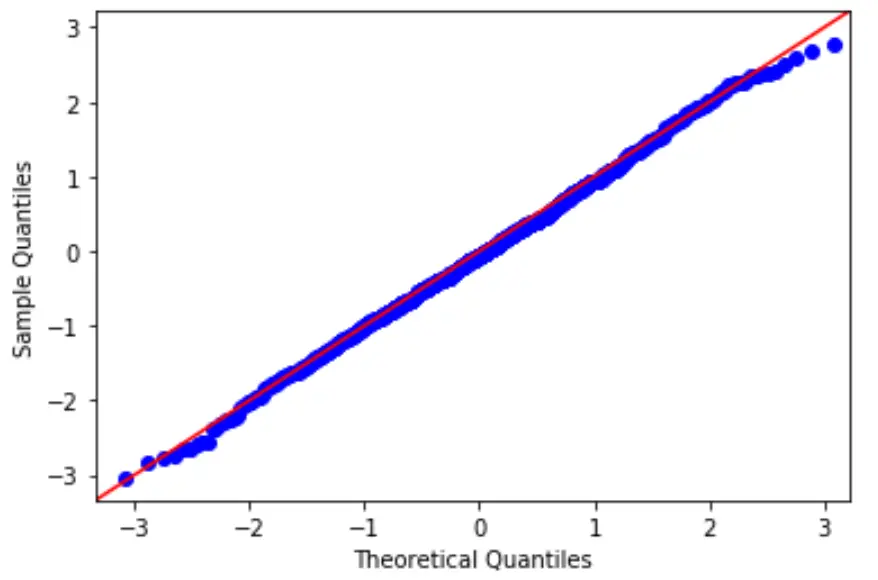
この仮説を検証するには、QQ プロットを作成します。これは、モデルの残差が正規分布に従うかどうかを判断するために使用できるプロットの一種です。
プロット上の点がほぼ直線の対角線を形成している場合は、正規性の仮定が満たされています。
3. 等分散性の仮定を確認します。
線形回帰のもう 1 つの重要な仮定は、x の各レベルで残差の分散が一定であるということです。これを等分散性といいます。そうでない場合、残差は不均一分散性の影響を受けます。
この仮定が満たされているかどうかを確認するには、 残差プロットを作成します。これは、モデルの予測値に対する残差を示す散布図です。
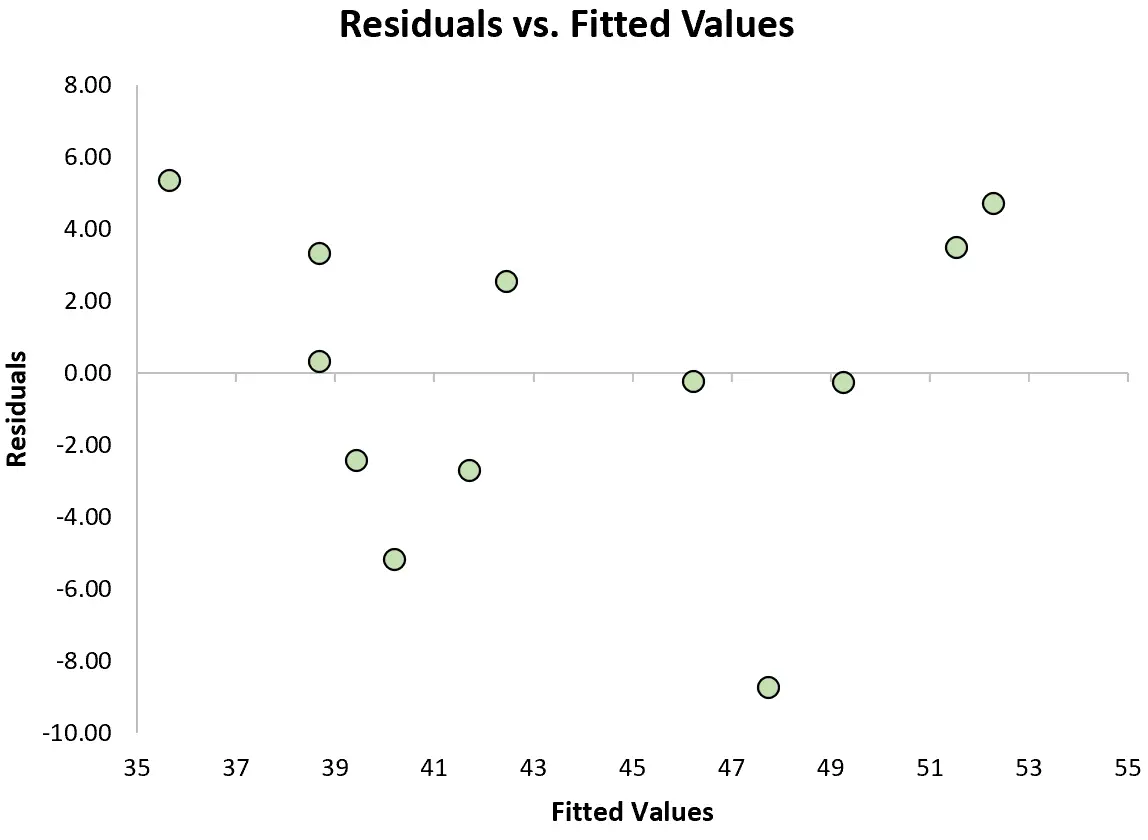
明確な傾向がなく、残差がグラフのゼロ付近にほぼ均等に分布している場合、一般に等分散性の仮定が満たされていると言われます。