比率の差の標本分布

によるベンジャミン・アンダーソン博士 8月 3, 2023 統計 0コメント

この記事では、比例標本分布の違いとは何か、またそれが統計で何に使用されるのかについて説明します。比率の違いによるサンプリング分布の式と、段階的に解く練習問題も示されています。

比率の差の標本分布はどのようなものになるでしょうか?

比率の差の標本分布は、2 つの異なる母集団から得られるすべての標本の標本比率の差を計算して得られる分布です。

つまり、比率の差の標本分布を取得するプロセスは、まず 2 つの異なる母集団から可能なすべてのサンプルを抽出し、次に抽出された各サンプルの比率を決定し、最後にすべてのサンプル間の差を決定します。比率の差の比率。 2つの人口。したがって、これらの操作を実行した後に得られた結果のセットは、比率の差の標本分布を形成します。

統計学では、比率のサンプリング分布の差は、ランダムに選択された 2 つのサンプルのサンプル比率の差が母集団の比率の差に近い確率を計算するために使用されます。

➤参照:比率サンプリングの割り当て

比率の差の標本分布の公式

比率の差分サンプリング分布のために選択されたサンプルは、二項分布によって定義されます。これは、実際の目的では、比率は観測値の総数に対する成功したケースの比率であるためです。

それにもかかわらず、中心極限定理により、二項分布は正規確率分布に近似できます。したがって、比率の差の標本分布は、次の特性を持つ正規分布に近似できます。

$\begin{array}{c}\displaystyle\mu_{\widehat{p_1}-\widehat{p_2}}=p_1-p_2 \qquad \sigma_{\widehat{p_1}-\widehat{p_2}}=\sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}\\[6ex]\displaystyle N_{p}\left(p_1-p_2, \sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}\right) \end{array}$

注:比率の差の標本分布は、次の場合にのみ正規分布に近似できます。

$n_1\geq30$

、

$n_2\geq 30$

、

$n_1p_1\geq5$

、

$n_2p_2\geq5$

、

$n_1q_1\geq5$

そして

$n_2q_2\geq5$

。

したがって、割合の差の標本分布は正規分布に近似できるため、割合の差の標本分布の統計量を計算する式は次のようになります。

$Z=\cfrac{(\widehat{p_1}-\widehat{p_2})-(p_1-p_2)}{\displaystyle\sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}}$

金：

$\widehat{p_i}$

はサンプル比率 i です。
$p_i$

は人口 i の割合です。
$q_i$

は母集団 i が失敗する確率であり、

$q_i=1-p_i$

。
$n_i$

はサンプルサイズ i です。
$Z$

は、標準正規分布 N(0,1) によって定義される変数です。

この式は、比率の違いに関する仮説検定式に似ています。

割合の違いの標本分布の具体例

比率標本分布の差の定義とその公式を理解した後、以下の解決例を段階的に見て概念を理解することができます。

2 つの生産工場の精度を分析するとします。一方の工場では、生産された部品の 5% のみに欠陥が生じるように生産されているのに対し、もう一方の工場では欠陥部品の割合が 8% であるとします。最初の工場から 200 個の部品のサンプルを採取し、2 番目の工場から 280 個の部品のサンプルを採取した場合、最初の製造工場の欠陥の割合が 2 番目の工場の欠陥の割合よりも大きい確率はどれくらいですか?生産？

問題のすべてのデータを把握するには、まず各植物の適切に生産された部分の割合を計算します。

$\begin{array}{c}q_1=1-p_1=1-0,05=0,95\\[2ex]q_2=1-p_2=1-0,08=0,92\end{array}$

最初の工場の不良率が 2 番目の工場の不良率よりも高かった場合、次の式が成り立つことを意味します。

$\widehat{p_1}-\widehat{p_2}>0″ title=”Rendered by QuickLaTeX.com” height=”18″ width=”89″ style=”vertical-align: -4px;”> したがって、比率の差の標本分布確率を決定するには、上のセクションで説明した式を適用する必要があります。 <p class=$ $Z=\cfrac{(\widehat{p_1}-\widehat{p_2})-(p_1-p_2)}{\displaystyle\sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}}=\cfrac{0-(0,05-0,08)}{\displaystyle\sqrt{\frac{0,05\cdot 0,95}{200}+\frac{0,08\cdot 0,92}{280}}}=1,34$

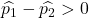
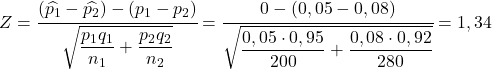
したがって、最初の工場の不良率が 2 番目の工場の不良率よりも大きい確率は、変数 Z が 1.34 よりも大きい確率と等価です。

$P[(\widehat{p_1}-\widehat{p_2})>0]=P[Z>1,34]” title=”Rendered by QuickLaTeX.com” height=”19″ width=”242″ style=”vertical-align: -5px;”> 最後に、<a href=$ 正規分布表で対応する確率を探すだけで、問題はすでに解決されています。

$P[(\widehat{p_1}-\widehat{p_2})>0]=P[Z>1,34]=0,0901″ title=”Rendered by QuickLaTeX.com” height=”19″ width=”319″ style=”vertical-align: -5px;”> つまり、第 1 工場の不良品の割合が第 2 工場の不良品の割合よりも大きい確率は 9.01% です。 <div style=$ ➤参照:平均の差の標本分布

著者について

ベンジャミン・アンダーソン博士

私はベンジャミンです。退職した統計教授から、専任の Statorials 教育者になりました。統計分野における豊富な経験と専門知識を活かして、私は Statorials を通じて学生に力を与えるために自分の知識を共有することに尽力しています。もっと知る

比率の差の標本分布はどのようなものになるでしょうか?

比率の差の標本分布の公式

割合の違いの標本分布の具体例

著者について

ベンジャミン・アンダーソン博士

コメントを追加する