ブリューシュ・パガン・テスト: 定義と例
線形回帰の重要な前提の 1 つは、予測変数の各レベルで残差が等しい分散で分布しているということです。この仮定は等分散性として知られています。
この仮定が尊重されない場合、残差に不均一分散性が存在すると言われます。これが起こると、回帰結果は信頼できなくなります。
不均一分散性が存在するかどうかを視覚的に検出する 1 つの方法は、回帰モデルからの近似値に対する残差のプロットを作成することです。
グラフ内の値が高くなるほど残差がさらに広がる場合、これは不均一分散性が存在することを示す明らかな兆候です。
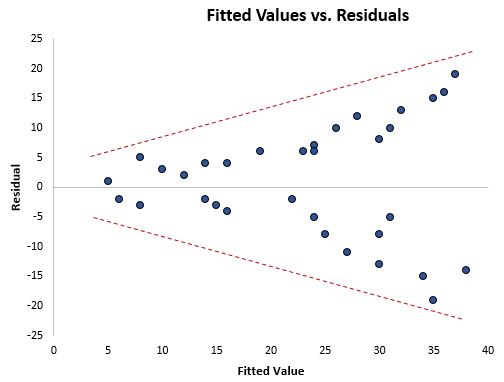
不均一分散性が存在するかどうかを判断するために使用できる正式な統計検定は、 Breusch-Pagan 検定です。
このチュートリアルでは、例とともに Breusch-Pagan テストの簡単な説明を提供します。
ブリューシュ・パガン・テストとは何ですか?
Breusch-Pagan 検定は、回帰モデルに不均一分散性が存在するかどうかを判断するために使用されます。
検定では次の帰無仮説と対立仮説を使用します。
- 帰無仮説 (H 0 ):等分散性が存在します (残差は等分散で分布します)
- 対立仮説 ( HA ):不均一分散が存在します (残差は等分散で分布していません)
検定の p 値が特定の有意水準(つまり、α = 0.05) を下回る場合、帰無仮説は棄却され、回帰モデルには不均一分散性が存在すると結論付けられます。
ブリューシュ・パガン・テストを実行するには、次の手順を使用します。
1.回帰モデルを当てはめます。
2.モデル残差の二乗を計算します。
3.残差の二乗を応答値として使用して、新しい回帰モデルを近似します。
4.カイ 2 乗 X 2検定統計量を n*R 2 newの形式で計算します。ここで、
- n:観測値の総数
- R 2 new :応答値として残差の二乗を使用した新しい回帰モデルの R 二乗
p (予測子の数) の自由度を持つこのカイ二乗検定統計量に対応する p 値が特定の有意水準 (つまり、α = 0.05) を下回る場合、帰無仮説は棄却され、不均一分散性が存在すると結論付けられます。 。
それ以外の場合は、帰無仮説を棄却しないでください。この場合、等分散性が存在すると仮定されます。
ほとんどの統計ソフトウェアは Breusch-Pagan 検定を簡単に実行できるため、これらの手順を手動で実行する必要はおそらくありませんが、舞台裏で何が起こっているかを知ることは役に立ちます。
ブリューシュ・パガン・テストの例
10 人の異なるバスケットボール選手に関する情報を含む次のデータセットがあるとします。
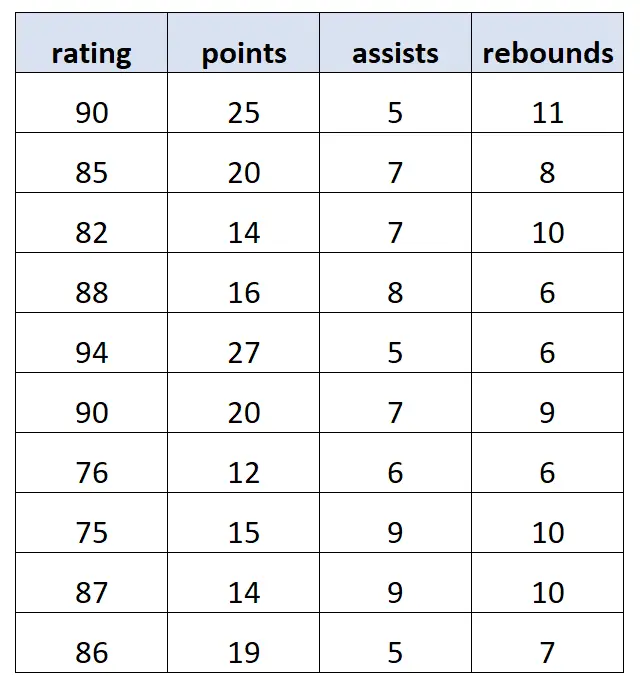
統計ソフトウェアを使用して、次の重線形回帰モデルを当てはめます。
スコア = 62.47 + 1.12*(ポイント) + 0.88*(アシスト) – 0.43*(リバウンド)
次に、このモデルを使用して各プレイヤーのレーティングを予測し、二乗残差 (つまり、予測レーティングと実際のレーティングの二乗差) を計算します。
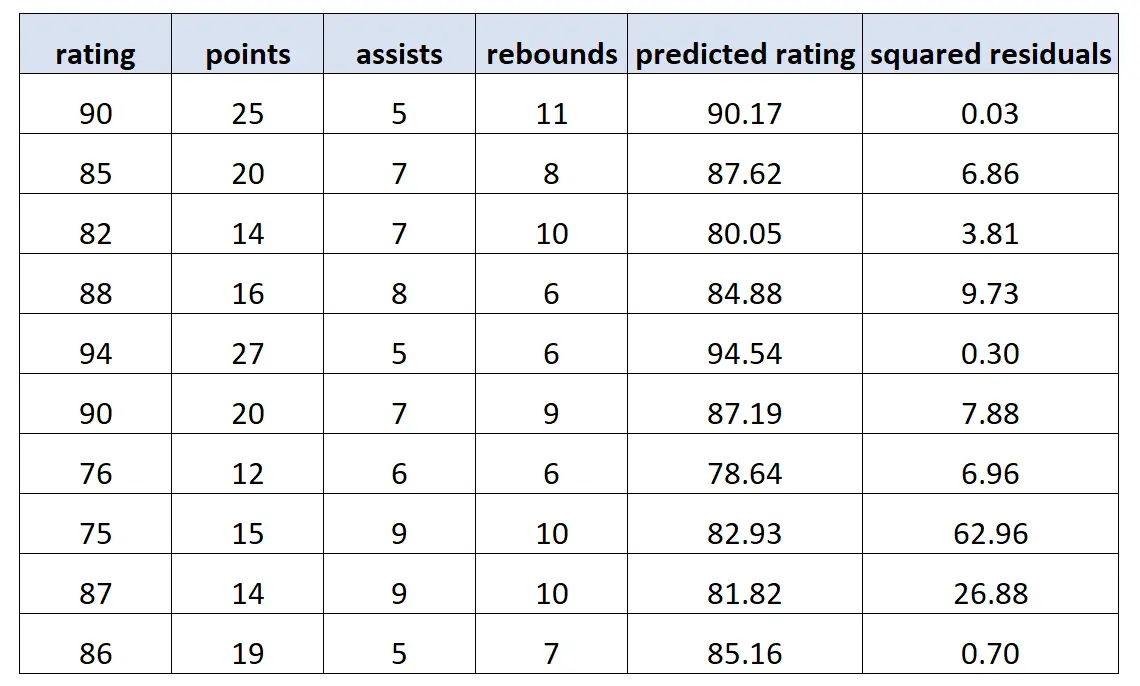
次に、残差の二乗を応答値として使用し、元の予測子変数を予測子変数として再度使用して、新しい回帰モデルを近似します。次のことがわかります。
- n: 10
- R2新規: 0.600395
したがって、Breusch-Pagan 検定のカイ 2 乗検定統計量は n*R 2 new = 10*.600395 = 6.00395となります。自由度はp = 3 の予測子変数です。
カイ 2 乗から P 値への計算によると、3 自由度の X 2 = 6.00395 に対応する p 値は0.111418です。
この p 値は 0.05 未満ではないため、帰無仮説を棄却できません。したがって、等分散性が存在すると仮定します。
実際のブリューシュ・ペイガン・テスト
次のチュートリアルでは、さまざまな統計プログラムで Breusch-Pagan 検定を実行する方法について、段階的な例を示します。
Excel でブルーシュ・ペイガン・テストを実行する方法
R で Breusch-Pagan テストを実行する方法
Python で Breusch-Pagan テストを実行する方法
Stata で Breusch-Pagan テストを実行する方法