相対頻度
この記事では、統計における相対度数とは何か、相対度数を取得する方法、および相対度数に関する 2 つの段階的な演習を学習します。
相対周波数とは何ですか?
統計学における相対頻度は、データ サンプル内に値が出現する回数を割合またはパーセンテージとして示す尺度です。より正確には、相対周波数は、絶対周波数をデータの総数で割ったものに等しくなります。
たとえば、値の絶対頻度が 15 で、データ ポイントが合計 100 個ある場合、その値の相対頻度は 0.15 (15/100=0.15) になります。
一般に、記号h i は相対周波数を表すために使用されます。統計コミュニティではまだ合意が得られていないため、相対頻度は別の記号で表されることがわかります。
相対周波数の計算方法
相対周波数は、絶対周波数をデータの総数で割ったものと等しくなります。したがって、相対頻度を計算するには、まず絶対頻度を見つけて、それを観測値の合計数で割る必要があります。
したがって、相対頻度の公式は次のようになります。
![]()
金:
-
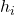
は相対周波数です。
-

は絶対周波数です。
-

はデータの総数です。
一方、パーセントで相対頻度を計算するには、つまり、パーセントで表される相対頻度を計算するには、前の式に 100 を掛けるだけです。
![]()
相対周波数の例
相対周波数の定義を理解したら、以下に 2 つの実際の例を示し、このタイプの周波数がどのように計算されるかを確認します。最初の例では離散変数の相対周波数が決定され、2 番目の例では連続変数が決定されます。
例 1: 離散変数
- 30人学級における統計科目の成績は以下の通りです。各音符の相対周波数はどれくらいですか?
![]()
![]()
![]()
データは整数のみであるため、この演習の変数は離散的です。したがって、データを間隔にグループ化する必要はありません。
相対周波数を求めるには、まず絶対周波数を決定する必要があります。そこで、頻度テーブルを作成し、異なる値ごとに絶対頻度を計算します。

絶対周波数を計算したので、次は相対周波数を計算します。これを行うには、各絶対周波数をデータの総数 (30) で割るだけです。
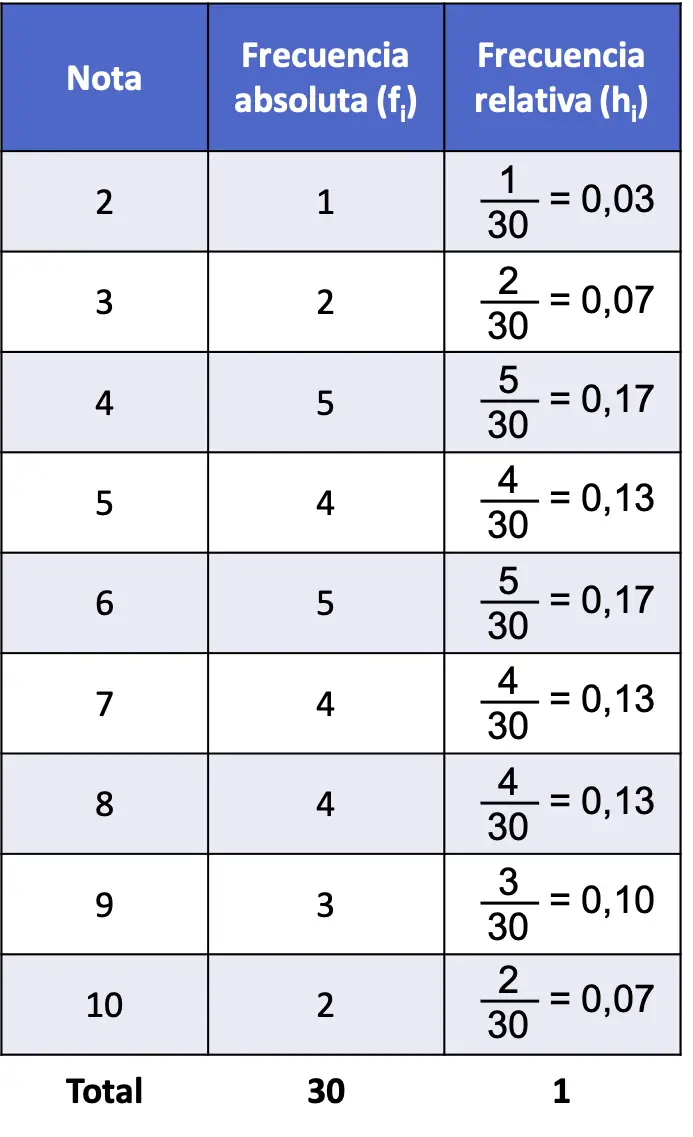
したがって、絶対周波数と相対周波数の問題の頻度表は次のようになります。

すべての相対度数の合計は常に 1 になることに注意してください。それ以外の場合、これは一部の計算が間違っていることを意味します。
例 2: 連続変数
- 20名の身長を測定したところ、以下の結果が得られました。データを間隔に分割し、各間隔の相対頻度を求めます。
![]()
![]()
この統計サンプルのデータは 10 進数であり、変数は任意の値を取ることができるため、連続変数に属します。したがって、周波数の計算を行う前に、まずデータを振幅が 10 分の 1 の間隔にグループ化します。
次に、各間隔の絶対頻度を含む頻度テーブルを作成します。

絶対頻度が見つかったら、その絶対頻度をデータの総数 (20) で割ることで、各間隔の相対頻度を取得できます。

累積相対度数
名前が示すように、累積相対頻度は統計で使用される別の種類の頻度であり、相対頻度から計算されます。
より正確には、値の累積相対頻度は、値自体の相対頻度と、より小さいすべての値の相対頻度の合計に等しくなります。
累積相対度数がどのように取得されるかを確認できるように、最初の例のデータセットの累積相対度数は以下のように計算されています。
