相関と回帰: 違いは何ですか?
相関と回帰は関連する 2 つの統計用語ですが、完全に同じというわけではありません。
このチュートリアルでは、両方の用語について簡単に説明し、それらがどのように似ていて異なるのかを説明します。
相関関係とは何ですか?
相関は、2 つの変数xとyの間の線形関連性を測定します。 -1 から 1 までの値を持ちます。ここで、
- -1 は、2 つの変数間の完全な負の線形相関を示します。
- 0 は 2 つの変数間に線形相関がないことを示します
- 1 は、2 つの変数間の完全な正の線形相関を示します。
たとえば、2 つの変数 (1) 学習時間と (2) 20 人の異なる学生が受け取った試験の得点を含む次のデータ セットがあるとします。

勉強時間と試験結果の散布図を作成すると、次のようになります。
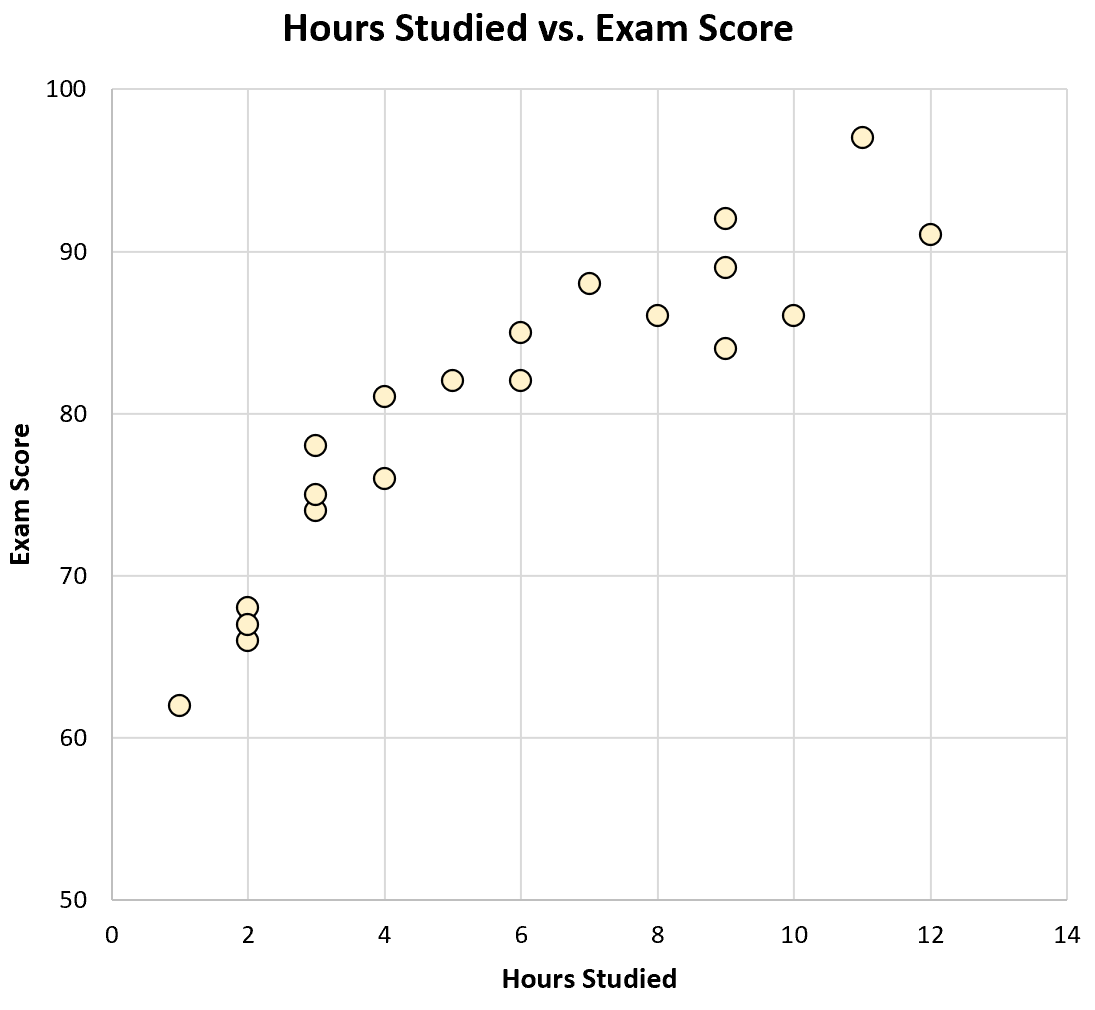
グラフを見るだけでも、より多く勉強した生徒は試験の成績が良い傾向にあることがわかります。言い換えれば、2 つの変数間に正の相関関係があることが視覚的にわかります。
計算機を使用すると、これら 2 つの変数間の相関関係が r = 0.915であることがわかります。この値は 1 に近いため、2 つの変数間に強い正の相関関係があることが確認されます。
回帰とは何ですか?
回帰は、変数xの値の変更が変数yの値にどのような影響を与えるかを理解するために使用できる方法です。
回帰モデルでは、1 つの変数xを予測変数として使用し、もう 1 つの変数y を応答変数として使用します。次に、2 つの変数間の関係を最もよく表す次の形式の方程式を見つけます。
ŷ = b 0 + b 1 x
金:
- ŷ:応答変数の予測値
- b 0 :原点の縦座標 (x が 0 に等しいときの y の値)
- b 1 :回帰係数 (x の 1 単位の増加に対する y の平均増加)
- x:予測変数の値
たとえば、以前のデータセットを考えてみましょう。

線形回帰計算機を使用すると、次の方程式がこれら 2 つの変数間の関係を最もよく表していることがわかります。
予想される試験スコア = 65.47 + 2.58*(勉強時間)
この式を解釈する方法は次のとおりです。
- ゼロ時間勉強した生徒の予想試験スコアは65.47です。
- 追加の 1 時間の学習に伴う試験の平均得点増加は2.58です。
この方程式を使用して、学習時間数に基づいて生徒が受け取るスコアを予測することもできます。
たとえば、6 時間勉強した生徒の成績は80.95になるはずです。
試験の予想スコア = 65.47 + 2.58*(6) = 80.95 。
この方程式を散布図上に線としてプロットすることもできます。
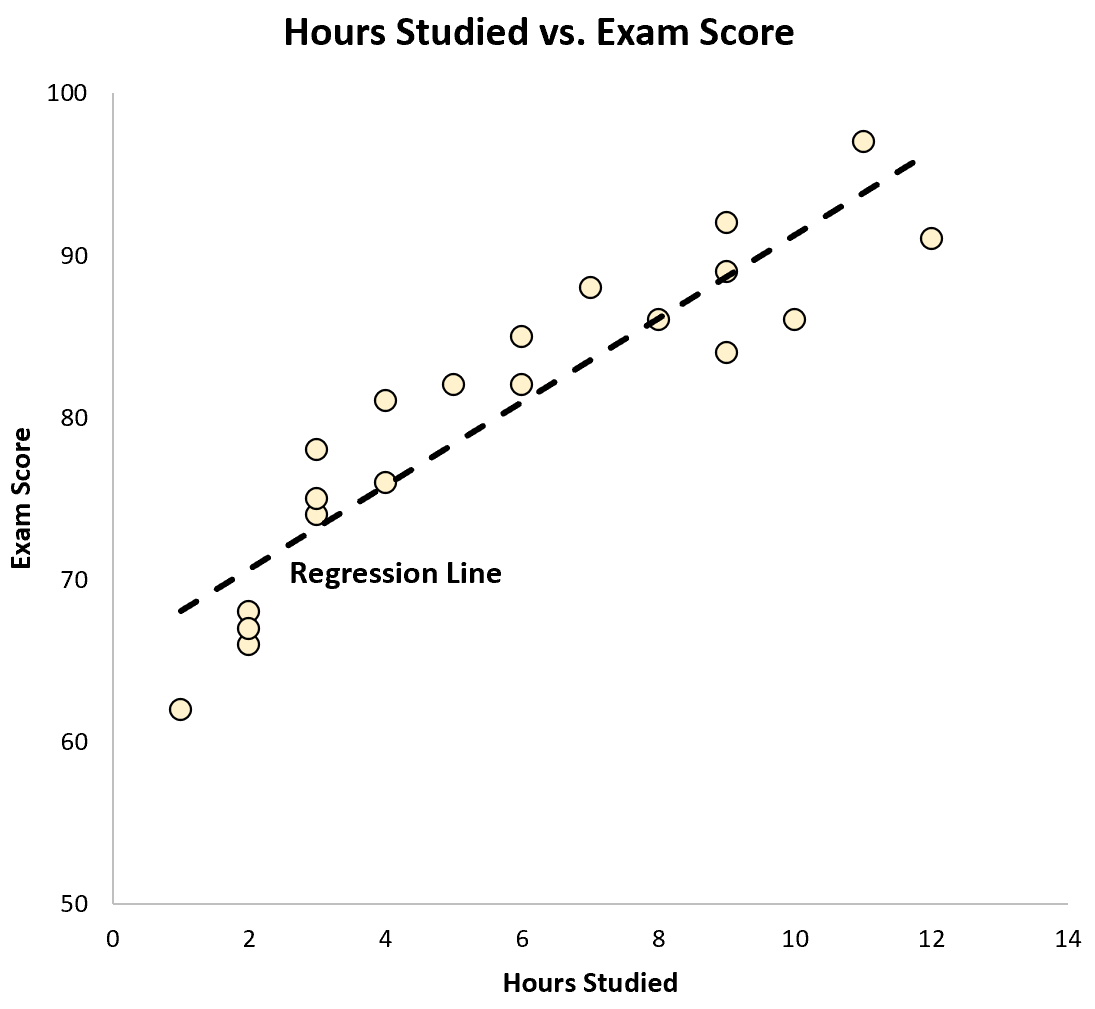
回帰直線がデータに非常によく「適合」していることがわかります。
これら 2 つの変数間の相関が r = 0.915であったことを思い出してください。この値を二乗すると、予測変数によって説明できる応答変数の分散の合計割合を表す「r 二乗」と呼ばれる数値が得られることがわかります。
この例では、r 2 = 0.915 2 = 0.837 です。これは、試験の得点の変動の 83.7% が勉強時間によって説明できることを意味します。
相関と回帰: 類似点と相違点
以下に、相関と回帰の類似点と相違点をまとめます。
類似点:
- どちらも 2 つの変数間の関係の方向を定量化します。
- どちらも 2 つの変数間の関係の強さを定量化します。
違い:
- 回帰では、2 つの変数間の原因と結果の関係を示すことができます。相関関係ではそれができません。
- 回帰では、方程式を使用して、ある変数の値を別の変数の値に基づいて予測できます。相関関係ではそれができません。
- 回帰では、方程式を使用して 2 つの変数間の関係を定量化します。相関には単一の数値が使用されます。
追加リソース
次のチュートリアルでは、この記事で取り上げるトピックについてさらに詳しく説明します。