算術平均
ここでは、算術平均とは何か、またその計算方法について説明します。算術平均の例や、統計サンプルの算術平均を求めるための計算ツールも用意されています。最後に、このタイプの平均の特性と、間隔にグループ化されたデータを使用して算術平均がどのように取得されるかを確認できます。
算術平均とは何ですか?
算術平均は、一連の統計データの中心値特性です。算術平均を計算するには、すべての値を加算し、データの総数で割ります。
さらに、算術平均は、サンプルの統計的研究を実行するために使用される主要な指標の 1 つです。
したがって、算術平均の式は次のようになります。
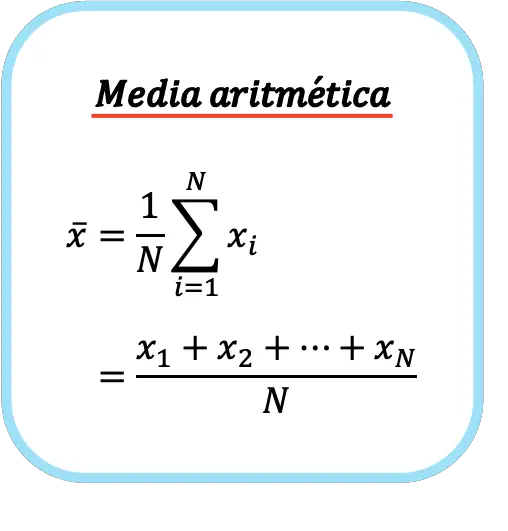
算術平均の記号は、文字 x の上にある水平の帯です。
![]()
平均値記号を使用して標本の平均と母集団の平均を区別することもできます。標本の平均は記号で表されます。
![]()
一方、母集団の平均にはギリシャ文字を使用します。
![]()
母集団の算術平均は統計変数の期待値に等しいことに注意してください。
算術平均とも呼ばれる算術平均が存在する唯一のタイプの平均ではなく、加重平均、二乗平均、幾何平均、調和平均などもあります。それぞれの計算方法は、当社 Web サイトの検索エンジンで確認できます。
算術平均の計算方法
算術平均を計算するには、次の手順を実行する必要があります。
- サンプルからのすべての統計データを追加します。
- 前の合計をデータの総数で割ります。
- 得られる結果は、統計サンプルの算術平均です。
👉以下の計算機を使用して、任意のデータセットの算術平均を計算できます。
算術平均の計算例
算術平均の定義を考慮して、例を段階的に解くことで、データセットの算術平均を取得する方法を見ていきます。
- 学生は学年中に次の成績を達成しました:数学で 9、言語で 7、歴史で 6、経済で 8、科学で 7.5。あなたのすべての成績の算術平均はいくらですか?
算術平均を求めるには、すべての成績を合計し、コース内の科目の総数である 5 で割る必要があります。したがって、算術平均の公式を適用します。
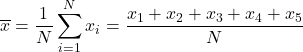
データを式に代入し、算術平均を計算します。
![]()
ご覧のとおり、算術平均では、各値に同じ重みが割り当てられます。つまり、各データは全体の中で同じ重みを持ちます。
算術平均計算機
統計サンプルのデータを次の計算機に入力して、算術平均を計算します。データはスペースで区切られ、小数点としてピリオドを使用して入力する必要があります。
グループ化されたデータの算術平均
グループ化されたデータとは、データがグループまたは間隔として構造化されていることを意味します。これは通常、統計サンプル サイズが非常に大きい場合に発生します。
したがって、概念は同じであっても、データがグループ化されている場合、算術平均の計算は少し異なります。
区間にグループ化されたデータの算術平均を計算するには、各グループのクラス スコアにその絶対頻度を乗算し、すべての絶対頻度の合計で割る必要があります。
![]()
注:区間のクラス スコアは、区間のエンドポイントの合計を 2 で割ることによって計算されます。たとえば、区間 [3,7) のクラス ノートは次のようになります。
![]()
これがどのように行われるかを理解できるように、区間にグループ化されたデータの算術平均に関する解決済みの演習を以下に示します。
- 私たちはグループの重みを統計的に研究したいと考えています。このために、81 人の代表的なグループにインタビューし、次のデータを取得しました。
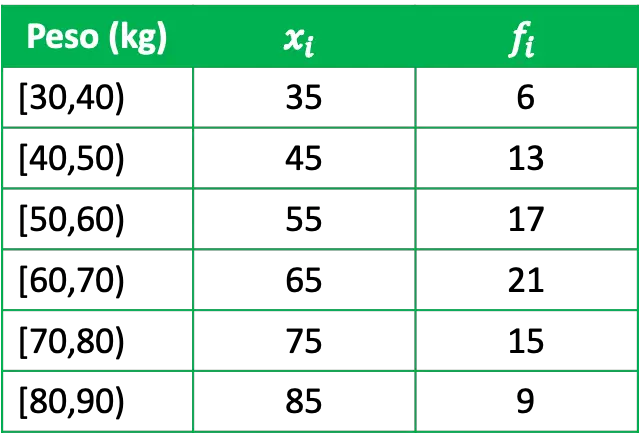
ここで、x iは各グループのクラス スコア、f iはその絶対頻度、つまり、この間隔で重みをもつ人の数です。
算術平均を求めるには、クラスノートとそれぞれの絶対頻度の積である列を頻度表に追加する必要があります。
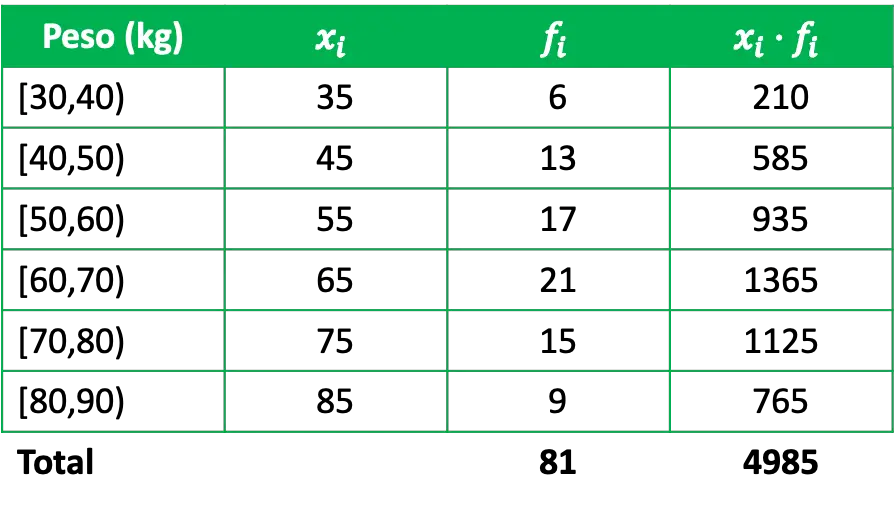
したがって、グループ化されたデータの算術平均を計算するには、クラスノートの頻度による積の合計をデータの総数で割るだけです。
![]()
算術平均の性質
算術平均には次の特性があります。
- 分布内のすべてのデータの平均からの偏差の合計はゼロになります。
![]()
- サンプル内のすべてのデータに同じ量を追加すると、サンプル平均はその量だけ増加します。
- 同じことが乗算でも起こります。サンプル内のすべての値に数値を乗算すると、サンプルの平均値にその数値が乗算されます。
- 算術平均は量的変数でのみ計算できます。言い換えれば、質的変数の平均を取ることはできません。
- 算術平均は常に分布の最小値と最大値の間の値になります。
![]()
- このタイプの平均は、非常に高い値または非常に低い値に非常に敏感であり、外れ値によって算術平均の結果が大きく変化します。
- データセットの算術平均は、常に同じデータセットの幾何平均以上です。
![]()
Excelで算術平均を計算する
Excel での算術平均の計算は、シートにデータを入力してAVERAGE関数を使用するだけなので、非常に簡単です。
たとえば、説明した最初に解いた演習のデータの算術平均を求めるには、すべてのデータを Excel ドキュメントにコピーし、次の数式をセルに書き込むだけです: =AVERAGE(9;7;5; 8;7) ,5) 。この関数はデータの算術平均 (7.3) を返します。
明らかに、特にサンプル サイズが非常に大きい場合は、手動で計算するよりも、Excel プログラムを使用して特定の数値の算術平均を見つける方がはるかに高速です。