箱ひげ図を比較する方法: 例付き
箱ひげ図は、データ セットの 5 桁の概要を表示するプロットの一種で、次のものが含まれます。
- 最小値
- 最初の四分位数 (25 パーセンタイル)
- 中央値
- 第 3 四分位数 (75 パーセンタイル)
- 最大値
箱ひげ図を作成するには、第 1 四分位から第 3 四分位までの箱を描きます。次に、中央値に垂直線を引きます。最後に、最小値と最大値までの四分位の「ひげ」を描画します。

箱ひげ図は、データセット内の値の分布をすぐに理解できるため便利です。 2 つの異なるデータセットを比較する場合にも役立ちます。
2 つ以上の箱ひげ図を比較する場合、次の 4 つの異なる質問に答えることができます。
1.中央値はどのように比較されますか?各ボックスの垂直線を比較して、どのデータセットがより高い中央値を持つかを判断できます。
2. 分散はどのように比較されますか?各ボックスの長さ (Q1 と Q3 の間の距離、つまり四分位範囲を表します) を比較して、どちらのデータ セットが大きいかを判断できます。
3. 非対称性はどのように比較されますか?垂直線が第 1 四半期に近づくほど、データセットはよりプラスに偏っています。垂直線が第 3 四半期に近づくほど、データセットの偏りは大きくなります。
4. 異常値は存在しますか?箱ひげ図では、外れ値は通常、各ひげを超えて広がる小さな円で表されます。観測値が次の基準のいずれかを満たす場合、その観測値は外れ値として定義されます。
- 1 つの観測値が Q1 未満 – 1.5*IQR
- 観測値が Q3 + 1.5*IQR より大きい
次の例は、2 つの異なる箱ひげ図を比較し、これら 4 つの質問に答える方法を示しています。
例: 箱ひげ図の比較
次のデータセットは、試験の準備のために 2 つの学習手法のいずれかを使用した学生の結果を示しています。
方法 1: 78、78、79、80、80、82、82、83、83、86、86、86、86、87、87、87、88、88、88、91
方法 2: 66、66、66、67、68、70、72、75、75、78、82、83、86、88、89、90、93、94、95、98
データセットごとに箱ひげ図を作成すると、次のようになります。
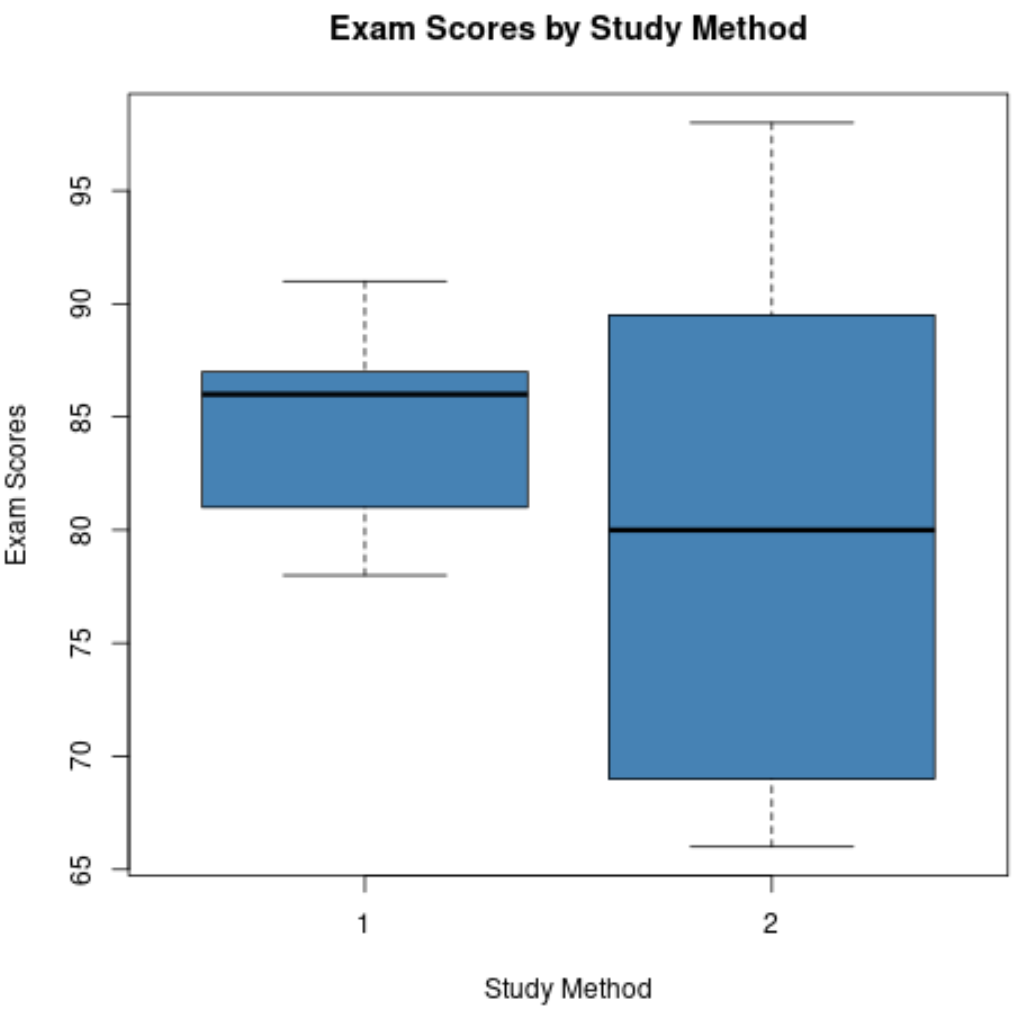
これら 2 つの箱ひげ図を比較すると、次の 4 つの質問に答えることができます。
1.中央値はどのように比較されますか?勉強法 1 の箱ひげ図の中央の線は、勉強法 2 の線よりも高く、勉強法 1 を使用した生徒の高等試験での成績中央値が高かったことを示しています。
2. 分散はどのように比較されますか?勉強方法 2 の箱ひげ図は、勉強方法 1 の箱ひげ図よりもはるかに長く、試験の得点が勉強方法 2 を使用した学生の間でより多く分散されていることを示しています。
3. 非対称性はどのように比較されますか?勉強法 1 の箱ひげ図の中央の線は Q3 に近く、勉強法 1 を使用した生徒の試験得点の分布が負に偏っていることを示しています。逆に、研究方法 2 の箱ひげ図の中央の線は箱の中心に近く、スコアの分布の歪みが最小限であることを意味します。
4. 異常値は存在しますか?どちらの箱ひげ図にも、上ヒゲや下ヒゲを超えて広がる小さな円はありません。これは、どちらのデータ セットにも明確な外れ値がないことを意味します。
追加リソース
Excel で箱ひげ図を作成および解釈する方法
SPSS で箱ひげ図を作成および解釈する方法
R で複数の箱ひげ図を作成する方法
Stata で箱ひげ図を作成および解釈する方法