統計グラフの種類

この記事では統計グラフの種類とその特徴について解説します。したがって、名前に加えて、存在するさまざまな種類のグラフの統計的用途もわかります。

統計グラフにはどんな種類があるの？

さまざまな種類の統計グラフは次のとおりです。

• 棒グラフ
• ヒストグラム
• 周波数ポリゴン
• 面グラフ
• パレート図
• ドットプロット
• 散布図
• 円グラフ
• ドーナツチャート
• 弾頭
• 年齢構成
• 箱ひげ図
• 放射状チャート
• 茎と葉の図
• 樹形図
• 絵文字
• カルトグラム

統計グラフの種類がわかったところで、それぞれがどのようなものかを見てみましょう。

棒グラフ

棒グラフは、離散変数をグラフ化するために使用される統計グラフの一種です。棒グラフでは、調査対象の変数の各値が X 軸上に表され、それぞれの頻度に比例した高さで長方形の棒が描画されます。

棒グラフは、棒が垂直に描かれている場合は垂直、棒が水平に描かれている場合は水平になります。

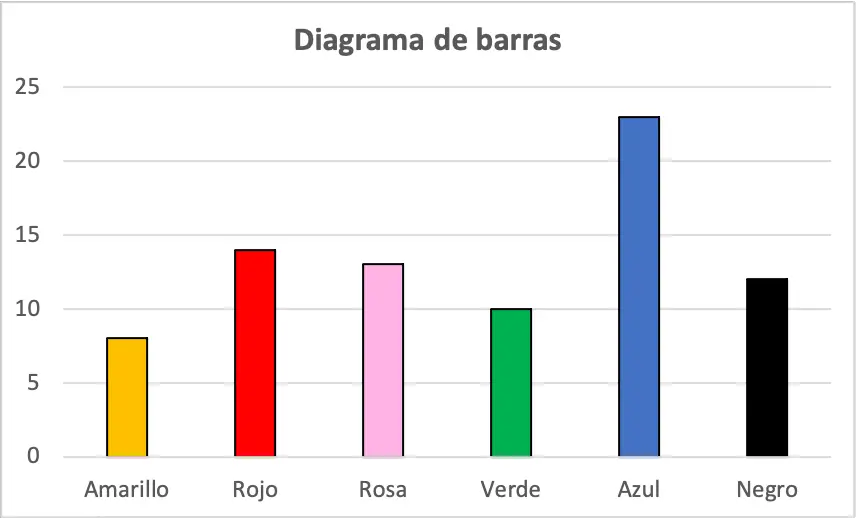
統計では、棒グラフはデータの繰り返し回数を比較するために使用されます。主に、質的変数のサンプル内のデータの頻度を分析するために使用されます。

このタイプの統計グラフは、棒グラフまたは縦棒グラフと呼ばれることもあります。

ヒストグラム

ヒストグラムは統計グラフの一種で、一連の統計データが長方形のバーで表され、ヒストグラム内の各バーが対応する頻度に比例します。

ヒストグラムは、統計サンプルの高さなどの連続変数をグラフ化するために使用されます。さらに、ヒストグラムを使用すると、分布の形状をすばやく視覚化できます。

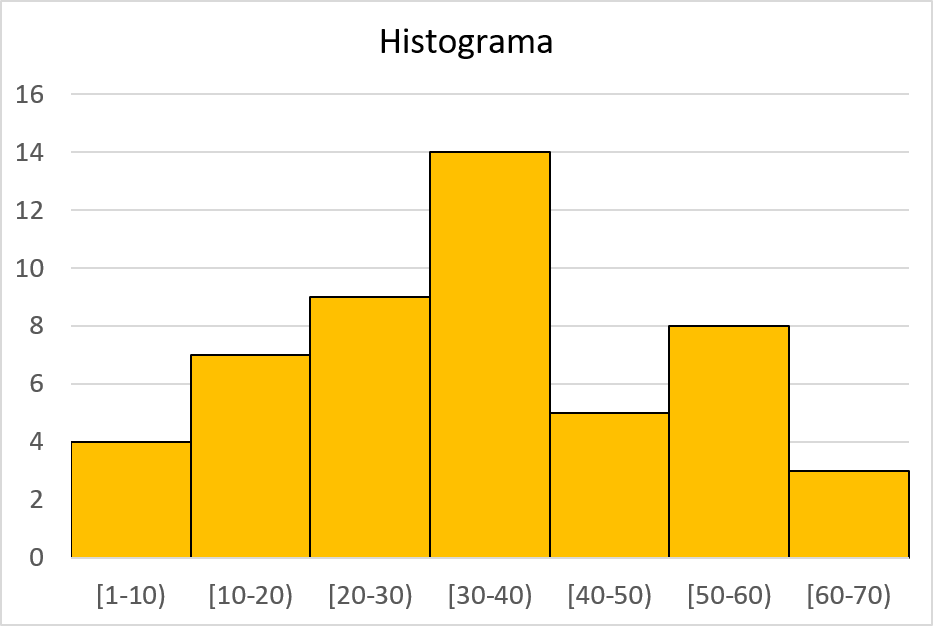
頻度ヒストグラムの各バーの幅は間隔の幅に比例し、高さは間隔の頻度に比例します。

棒グラフとヒストグラム (古いタイプの統計グラフ) の違いは、それらが表す変数のタイプです。棒グラフは離散的な質的変数をグラフ化するために使用され、ヒストグラムは連続的な量的変数を表すために使用されます。

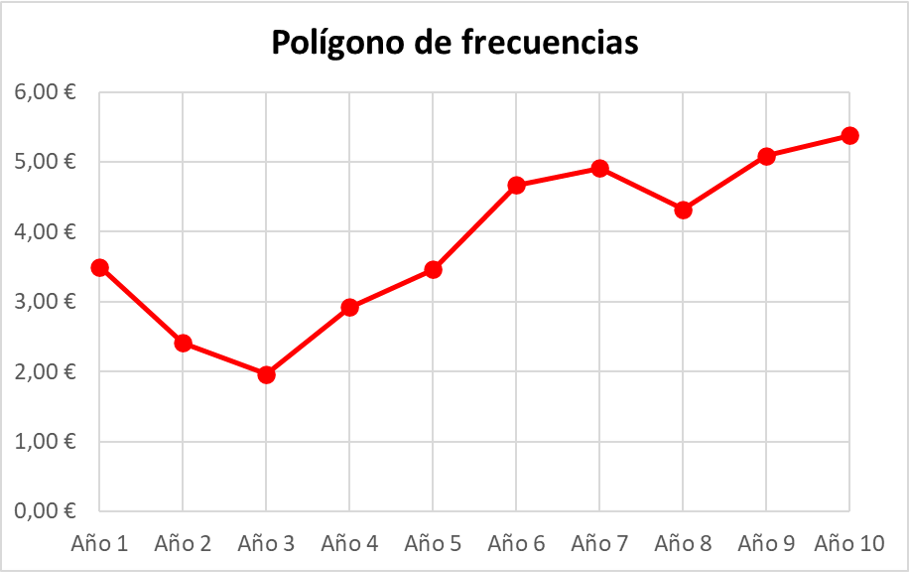
周波数ポリゴン

周波数ポリゴンは、一連のデータが点で表され、線で接続された統計グラフの一種です。

統計では、このタイプの図はデータの変化を分析するのに非常に役立つため、時系列を表すために頻度多角形が一般に使用されます。

面グラフ

面グラフでは、データは直線で結ばれた点で表され、グラフの下の領域が色付けされます。

したがって、面グラフは周波数多角形に似ていますが、さらにその下の領域がペイントされます。

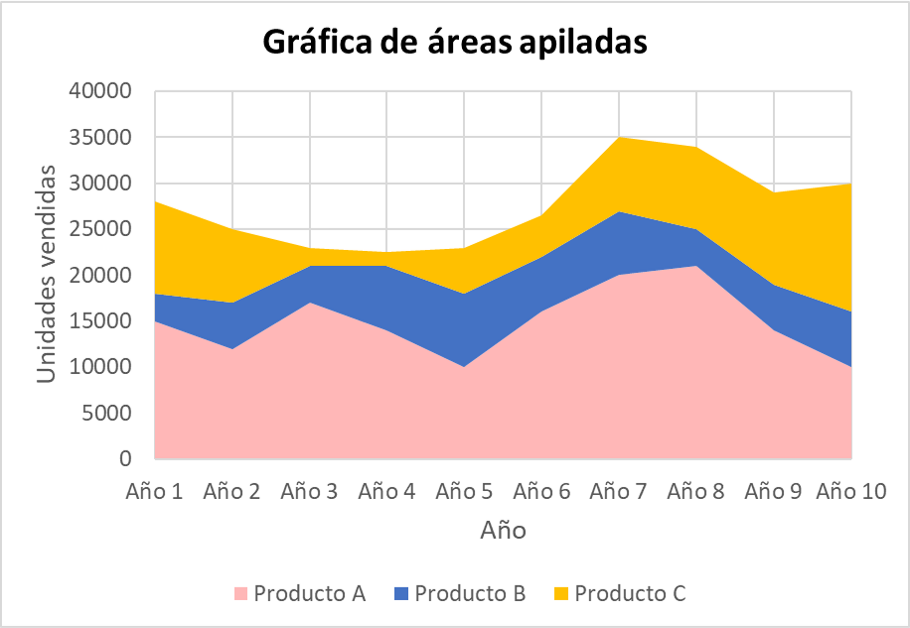
このタイプの統計グラフの利点は、複数のデータ系列を 1 つの図で表現できるため、それらを比較して合計値を把握することが容易になることです。

パレート図

パレート図は、ヒストグラムと度数多角形を組み合わせた統計図の一種です。パレート図では、一連のデータが棒を使用して降順で表されます。代わりに、累積パーセンテージが頻度多角形を使用してグラフに追加されます。

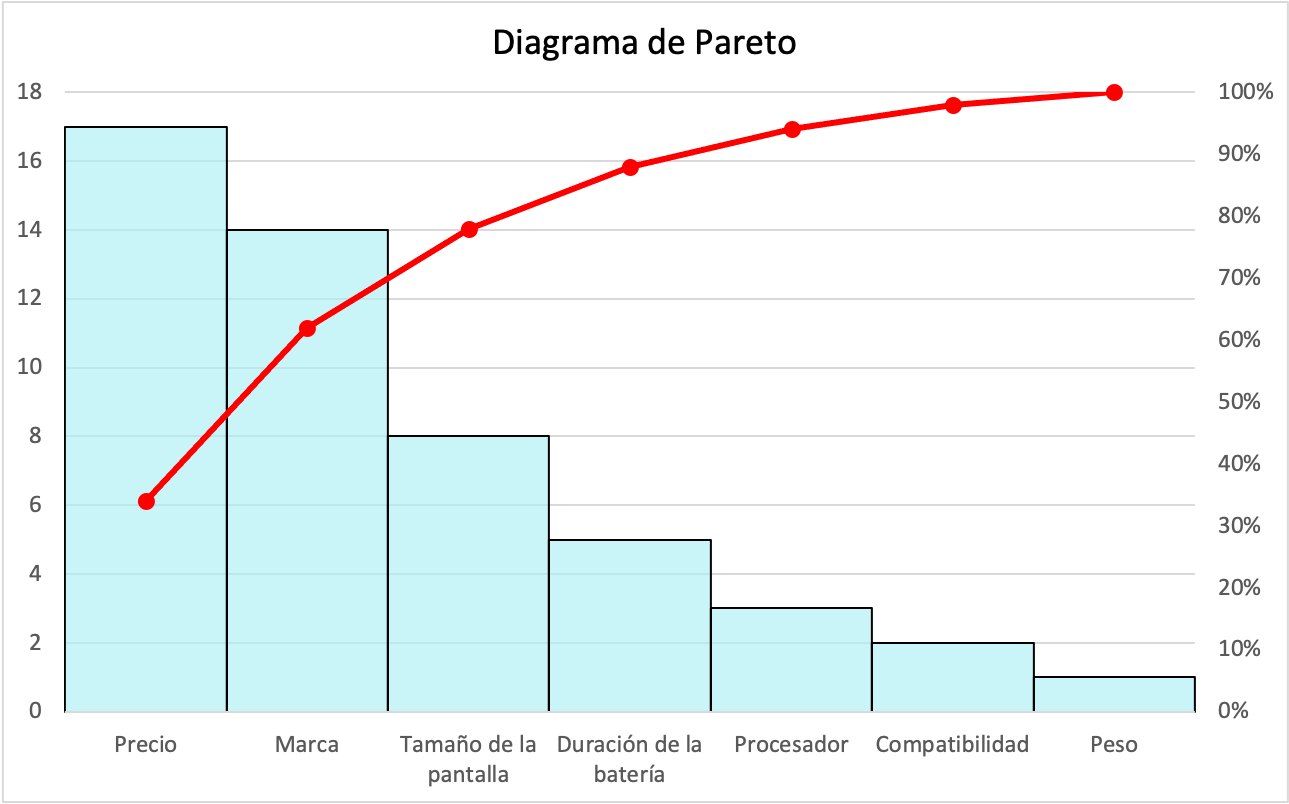
統計では、このタイプの図は問題を分析し、その主な原因を特定するために使用されます。また、絶対頻度と累積パーセンテージを同時に表示できるのも特徴で、問題の最も重要な原因の分析と特定に役立ちます。

ドットプロット

ドット プロットは、データを数直線に沿った点として表すために使用されるグラフです。したがって、ドット プロットはデータの位置と変動性を特定するために使用されます。

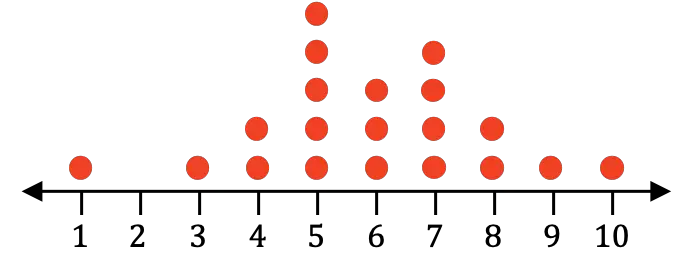
ドット プロットは、どのデータが最も頻繁に繰り返されるかを確認するために使用されるという点で、ヒストグラムと非常によく似ています。ただし、ドット プロットとヒストグラムの違いはデータの数です。ドット プロットは小さなデータ セットを表すのに適しており、一方、ヒストグラムは大きなデータ セットを表すのに適しているためです。

散布図

散布図は、2 つの変数のデータセットが 2 つのデカルト座標軸上にグラフ化される統計図の一種です。

したがって、散布図は 2 つの統計変数間の関係を分析するために使用されます。

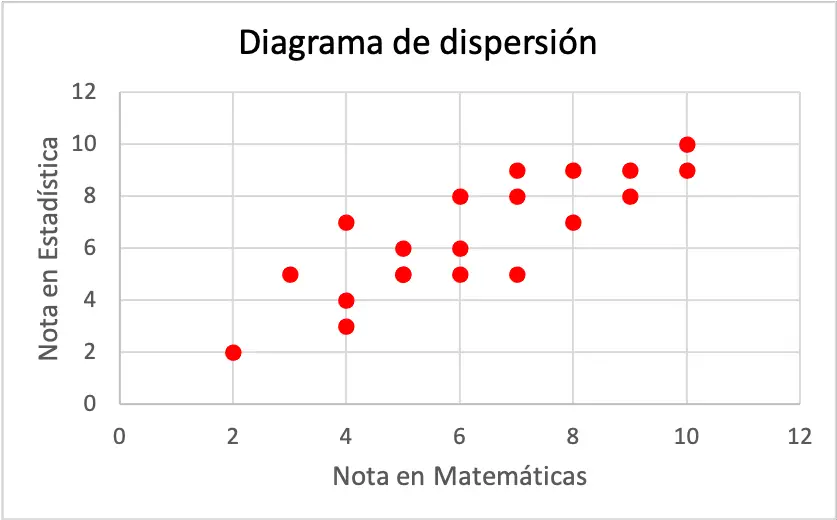
散布図には、相関図や散布図など、いくつかの異なる名前があります。

散布図は、パレート図、特性要因図、フローチャートなどと同様に、品質管理の基本ツールの 1 つとみなされていることに注意してください。

円グラフ

円グラフ、または円グラフ は、統計図の一種であり、データがセクターに分割された円によって表され、各セクターの角度が対応する頻度に比例します。

したがって、値の頻度が高くなるほど、図内の対応するセクターが大きくなります。

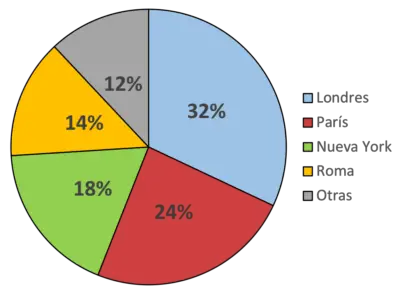
円グラフは、各値の頻度を視覚的に分析するために使用されます。統計では、これらのタイプのグラフは主に質的変数を表すために使用されます。

ドーナツチャート

ドーナツグラフはその名の通り、ドーナツのような形をした統計グラフの一種です。より具体的には、ドーナツ チャートは、各値が占めるリングの部分がその頻度に比例するように、一連のデータのパーセンテージを表すために使用されます。

したがって、値が大きいほど、ドーナツ グラフ内でその値が占める部分も大きくなります。

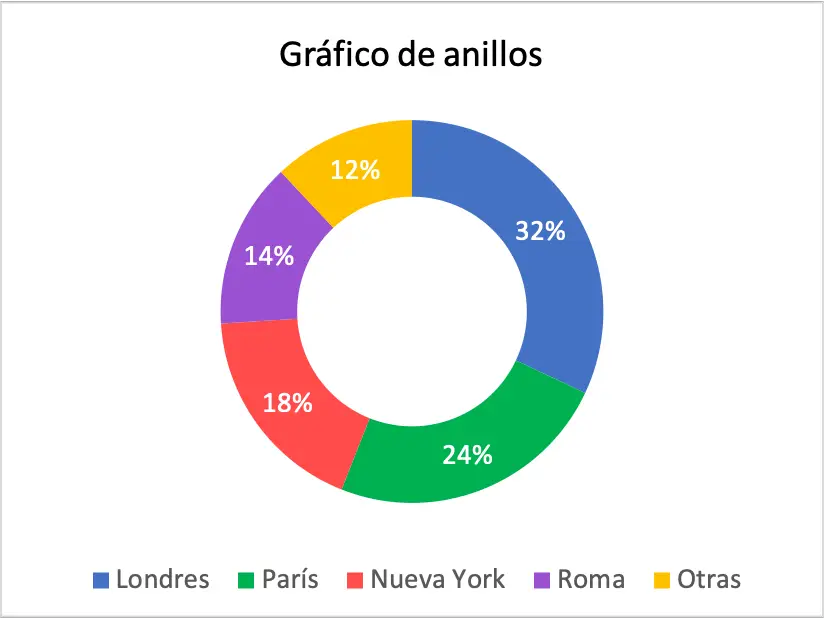
統計では、ドーナツ チャートは定性データをグラフ化するのに特に役立ちます。また、視覚的かつ魅力的な方法でパーセンテージをグラフ化するためにも使用されます。

弾頭

統計学では、オージブは一連のデータの累積グラフです。簡単に言えば、オージブは、一連のデータに関連付けられた累積頻度を示すグラフです。

したがって、弾頭は、特定の値を下回るデータの数を知るために使用されます。

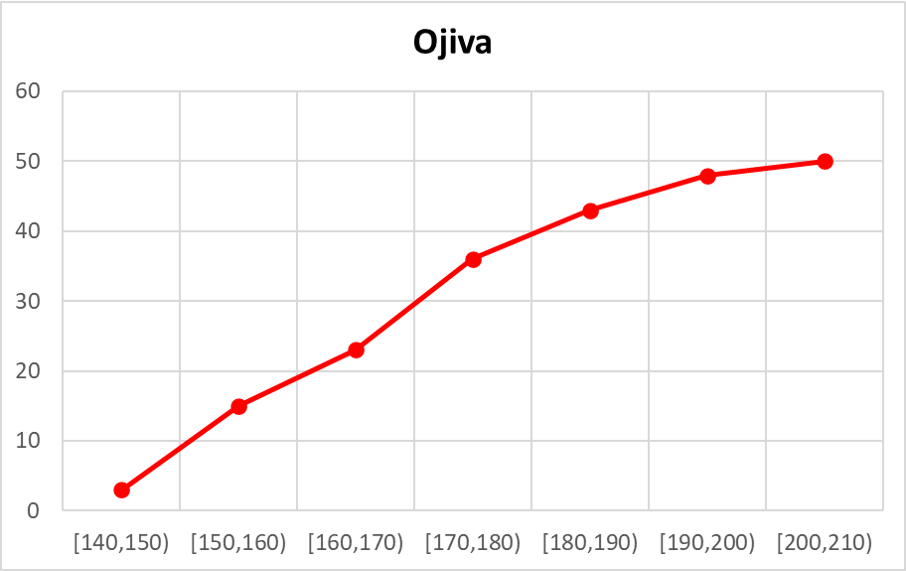
弾頭には量的変数のみを表すことができます。このタイプの統計図は、質的変数には役に立ちません。

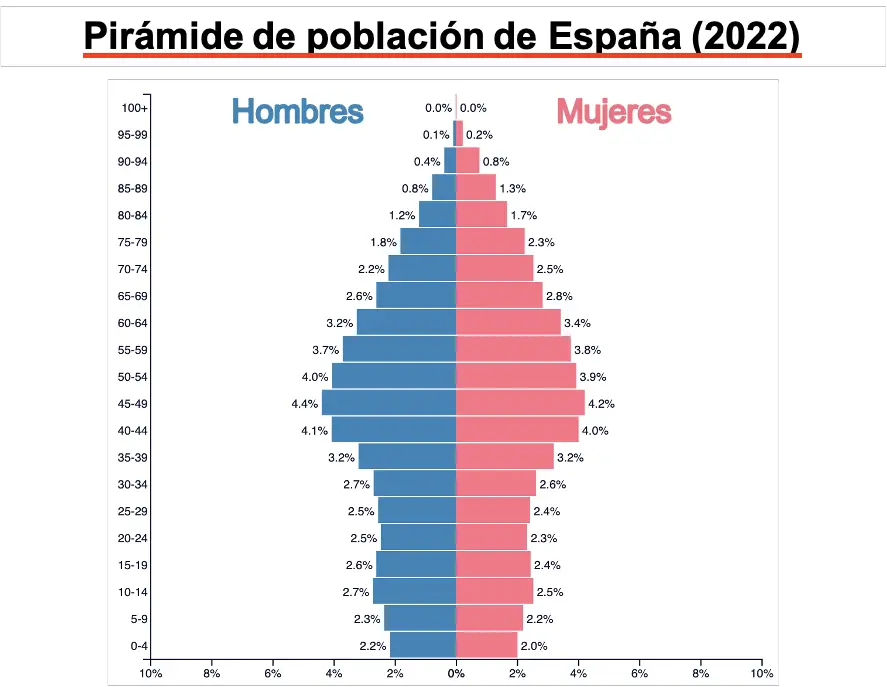
年齢構成

人口ピラミッド は、人口ピラミッドとも呼ばれ、人口の構造をグラフィカルに表現したものです。具体的には、人口ピラミッドを使用して、年齢と性別ごとに人口の割合を分析します。

通常、人口ピラミッドは国で構成されますが、論理的には、人口ピラミッドは都市、州などの任意の地域で構成できます。

箱ひげ図

箱ひげ図 は、箱ひげ図または箱ひげ図とも呼ばれ、四分位数を使用して一連の統計データを視覚的に表すグラフです。

箱ひげ図の主な特徴は、データの四分位数、中央値、極値、外れ値が表示されるため、データ系列の分散を迅速に視覚化できることです。

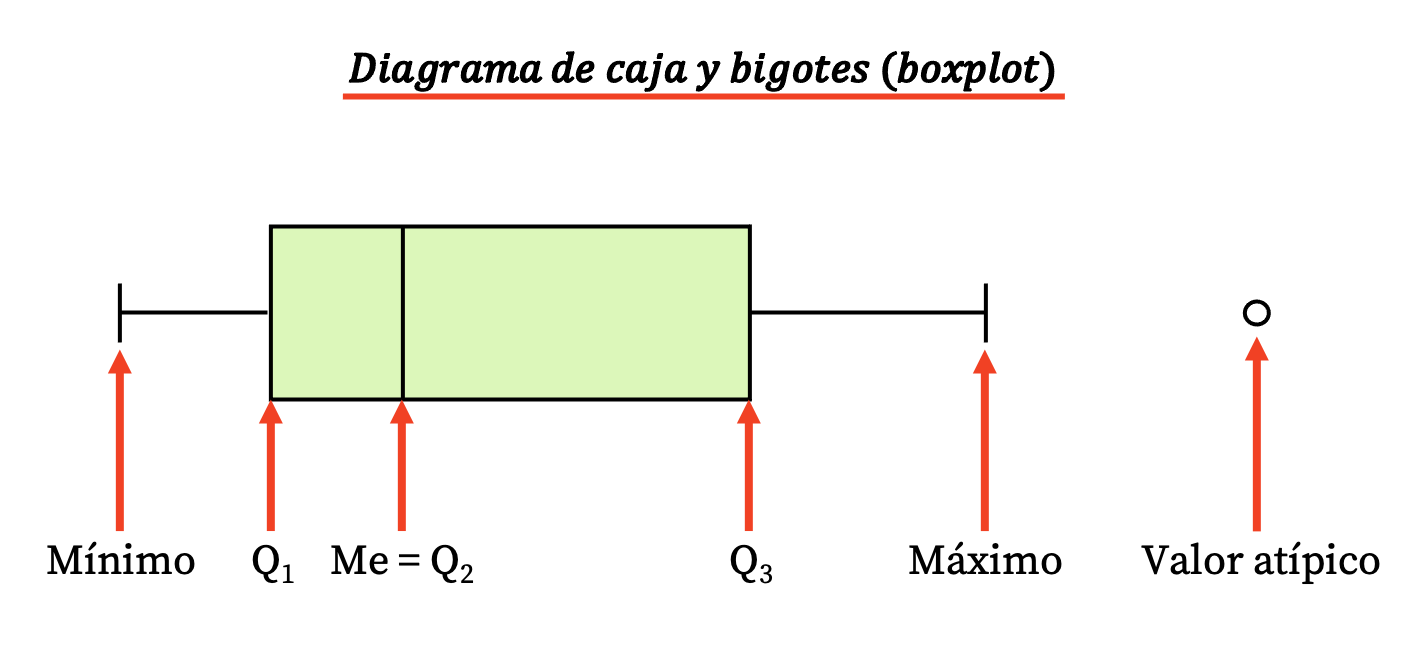
箱ひげ図は、数値変数を比較するのに非常に役立ちます。ただし、カテゴリ変数を表すには適していません。

放射状チャート

放射状チャートはスパイダー チャートとも呼ばれ、さまざまな変数が表される統計チャートの一種です。つまり、統計では、放射状グラフはさまざまな変数の値を比較するために使用されます。

さらに、放射状チャートの主な利点は、非常に視覚的であるため、変数を簡単かつ迅速に比較できることです。

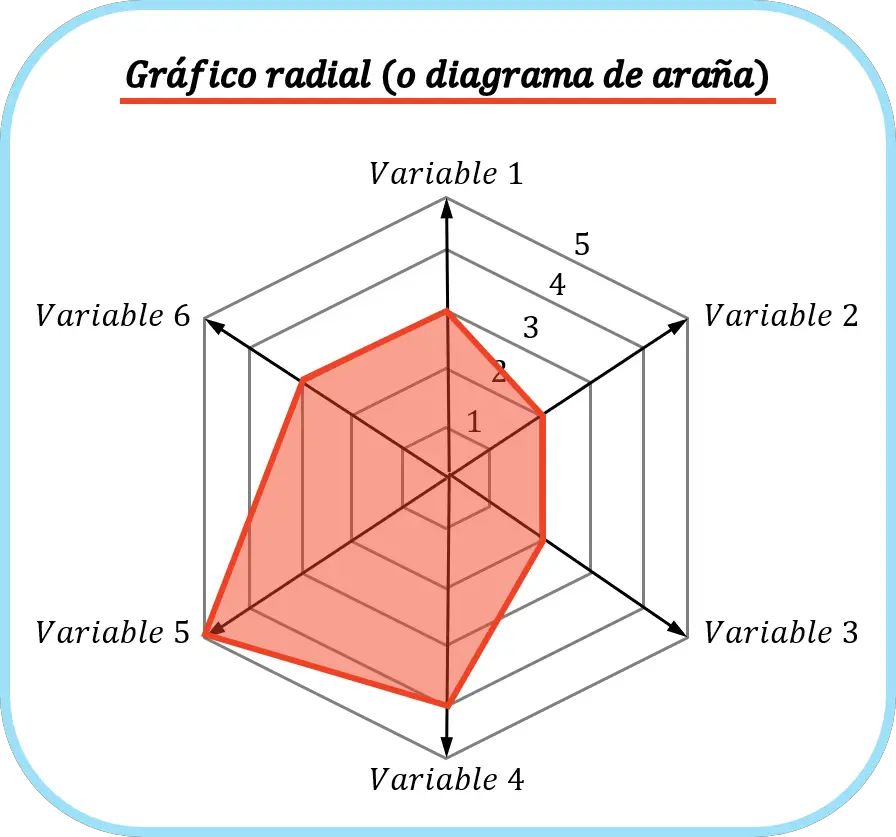
レーダー マップには、ネットワーク マップ、極マップ、スター マップなど、さまざまな名前があります。

茎と葉の図

幹葉図は、一連の定量的データを表す統計図の一種です。

幹葉プロットでは、各データ要素は、最後の桁である葉と、残りの桁に対応する幹によって区切られます。したがって、茎と葉の図では、各葉は対応する茎の線上に配置されます。

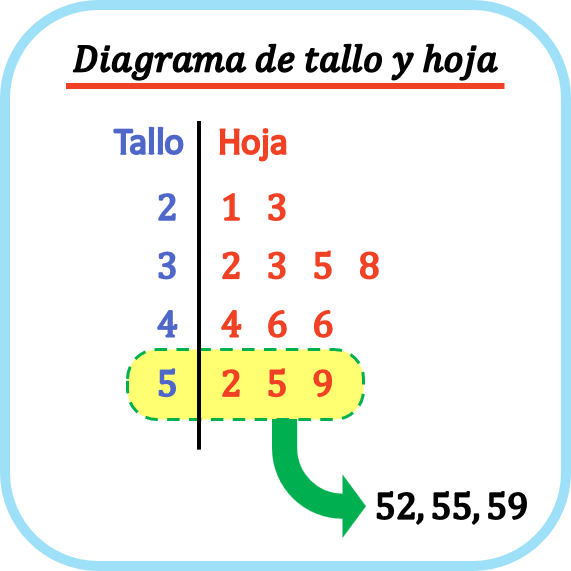
このように、茎と葉のプロットは、一連の統計データをグラフで表現するのに役立ち、分布の形状を視覚化するのにも役立ちます。

樹形図

樹形図 は、確率ツリーとも呼ばれ、実験で考えられるすべての結果とその確率をグラフで表現したものです。

したがって、樹状図を使用して、サンプル空間で考えられるすべての結果をグラフ化し、その確率を計算します。

最終結果に到達するまで、各結果 (ノード) が新しい結果 (ブランチ) に分岐するようにツリーが作成されます。

絵文字

統計学におけるピクトグラムは、データを図で表すグラフの一種です。簡単に言えば、ピクトグラムは、データの頻度を表すためにバーの代わりに画像を使用した図です。

したがって、ピクトグラムは、一連の統計データを視覚的にグラフィックで表現するために使用されます。

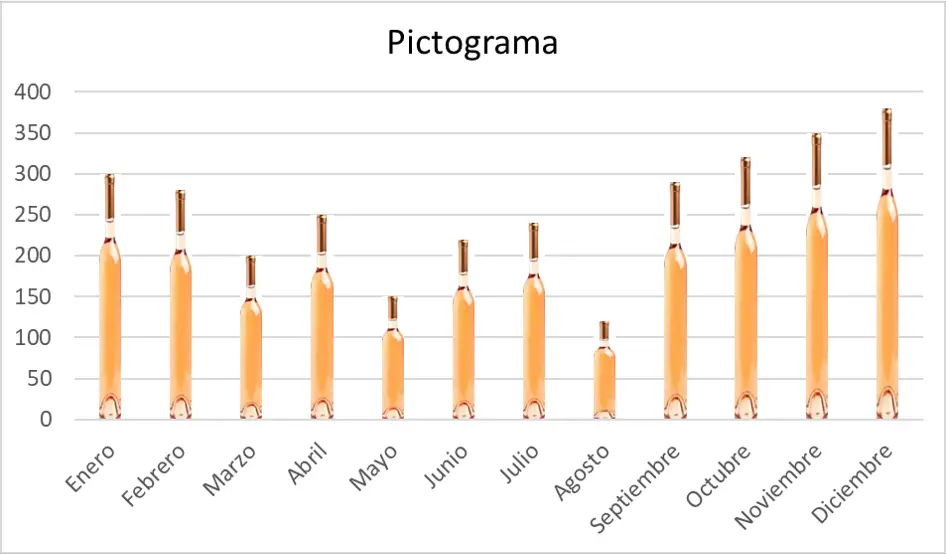
ピクトグラムは、定性変数または離散変数を表すために使用されます。

カルトグラム

カートグラムは、一連のデータをさまざまな色を使用して地図上に表現した統計グラフの一種です。簡単に言えば、カートグラムは各地理的領域に関連付けられたデータを示す図です。

たとえば、すべてのアフリカ諸国の住民の数が地図上にグラフ化されました。ご覧のとおり、各色は住民の数に対応しており、より正確には、色が濃いほど、この国の人口が多いことを意味します。

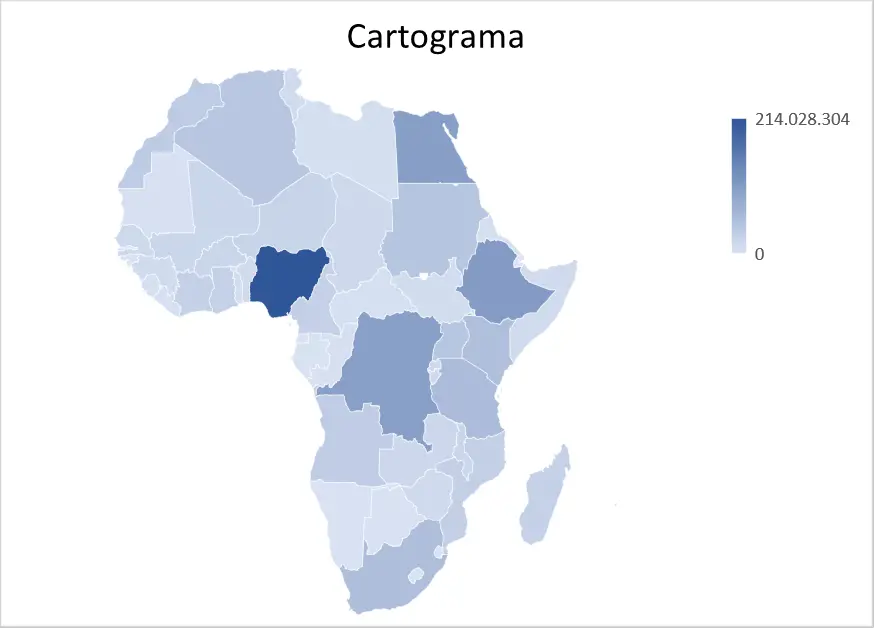
したがって、統計では、地理的領域に関連付けられた一連のデータをグラフィカルに表現するためにカートグラムが使用されます。