頻度(統計)
この記事では、統計における頻度の概念について説明します。したがって、統計における頻度の定義、存在するさまざまな種類の頻度、そして最後に頻度表の作成方法がわかります。
統計における頻度とは何ですか?
統計において、頻度はデータセット内に値が出現する回数です。簡単に言えば、頻度は統計サンプル内で値が繰り返される回数です。
たとえば、アンケートで 5 人が好きな色は青だと答えた場合、青の頻度は 5 に等しくなります。
一般に、統計では、インデックスiを持つ文字f は値iの頻度を表すために使用されるため、頻度の記号はfiになります。
すべての周波数の合計により、サンプル内のデータの総数が求められます。したがって、次の式はあらゆる統計研究に対して常に有効です。
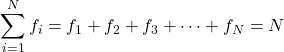
金
![]()
値の周波数です
![]()
そして
![]()
観測値の合計数です。
統計における度数の種類
統計では、さまざまな種類の頻度は次のとおりです。
- 絶対頻度: 統計サンプルに値が出現する回数に対応します。
- 累積絶対頻度: 値の絶対頻度と、より小さいすべての値の絶対頻度を加算することによって計算されます。
- 相対周波数: これは、絶対周波数をデータの総数で割ったものです。
- 累積相対頻度: 値の相対頻度と、それより低いすべての値の相対頻度の合計に等しくなります。
以下のセクションでは、各周波数タイプがどのように計算されるかを確認できます。
度数表
通常、統計では、データのサンプルの頻度の計算が頻度表にまとめられます。以下に段階的な例を示しますので、その方法を確認してください。
- 30人学級における統計科目の成績は以下の通りです。データセットの頻度表を作成します。
![]()
![]()
![]()
すべての数値は整数のみであるため、これは離散変数です。したがって、データを間隔にグループ化する必要はありません。
したがって、それぞれの異なる値が行となるテーブルを構築する必要があります。さらに、各値の絶対頻度を見つける必要があります。これを行うには、単にデータ サンプル内に値が出現する回数を数えます。

すべての絶対周波数の合計がデータの総数に等しいことに注意してください。このルールが守られない場合は、特定の情報を提供するのを忘れたことを意味します。
絶対周波数がわかったので、次は累積絶対周波数を見つける必要があります。この計算には 2 つのオプションがあります。値の絶対頻度と最小値のすべての絶対頻度を加算するか、その逆に、値の絶対頻度と前の値の累積絶対頻度を加算します。

最後の値の累積絶対頻度は常にデータの総数に対応するため、このトリックを使用して計算が正しいことを確認できます。
次に、相対頻度を決定する必要があります。相対頻度は、絶対頻度をデータ ポイントの総数 (30) で割ることによって計算されます。

すべての相対度数の合計は常に 1 に等しいことに注意してください。そうでない場合は、度数表の計算の一部が間違っていることを意味します。
最後に、累積された相対周波数を抽出するだけで十分です。これを行うには、問題の値の相対度数に以前のすべての相対度数を加えたもの、または同じことになりますが、以前に累積された相対度数を加算する必要があります。

つまり、問題のあるデータのすべての頻度を含む頻度表は次のとおりです。
