ランク(統計)
この記事では、統計における範囲とその計算方法について説明します。データセットの範囲に関する解決済みの演習があり、最後に、それが何のために、いつ使用されるべきかを示します。
統計における範囲とは何ですか?
統計学における範囲とは、サンプルのデータの最大値と最小値の差を示す分散の尺度です。したがって、母集団または統計サンプルの範囲を計算するには、最小値から最大値を減算する必要があります。
たとえば、データ セットの最大値が 9、最小値が 2 の場合、この統計サンプルの範囲は 7 (9-2=7) になります。
統計範囲は、測定の範囲または範囲とも呼ばれます。
したがって、範囲は、分散、標準偏差 (または標準偏差)、平均偏差、および変動係数を含む分散の尺度です。
統計における範囲の計算方法
サンプルの範囲は、統計サンプル データの極値を減算することによって計算されます。つまり、サンプルの範囲は、すべてのデータの最大値から最小値を引いたものに等しくなります。
したがって、データセットの統計範囲を計算する式は次のようになります。
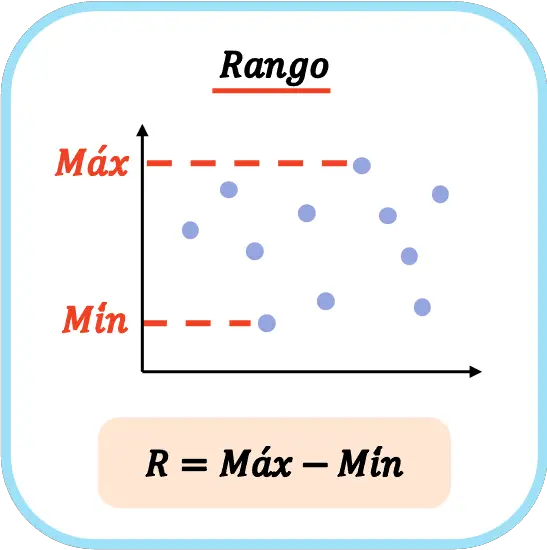
統計では、データ系列の範囲を示すために大文字の R の記号がよく使用されます。
したがって、極値間の差を決定するだけでよいため、データセットの範囲の計算は非常に簡単です。注意する必要があるのは、最大値と最小値のデータを正確に取得し、数値を忘れないことだけです。
範囲の例(統計)
統計における範囲の定義を確認した後、データセットの範囲がどのように取得されるかを確認できるように、以下に実際の例を示します。
- ある企業は、過去 20 年間に自社の主力製品が達成した売上を統計的に分析したいと考えています。これを行うために、ランキングを含むいくつかの統計的尺度を計算するよう求められます。製品の売上が次の表に示されている場合、このデータセットの範囲はどれくらいですか?
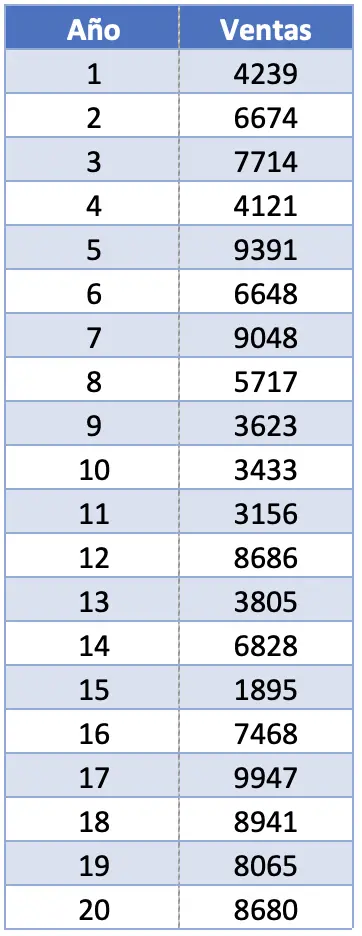
この演習では、20 個の観測値があります。実際には、最大値と最小値のみに関心があるため、サンプルの範囲を計算する際に観測値の総数は何の違いもありません。
したがって、この統計サンプルの範囲を見つけるには、上記の式を使用する必要があります。
![]()
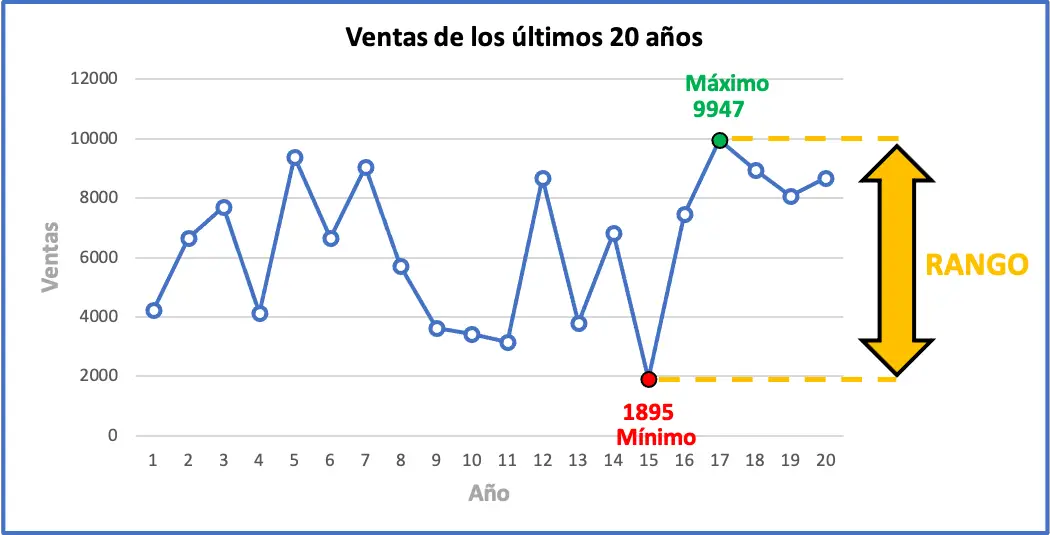
間隔の最大値は販売数 9947 で、最小値は 1895 です。したがって、データセットの範囲を見つけるには、これら 2 つの値を減算する必要があります。
![]()
これは、過去数年間の販売台数の最大変化が 8,052 台であることを意味します。以下に、すべての運動データとその統計範囲をグラフで表示できます。グラフは範囲の意味を理解するのに役立つでしょう。
統計範囲は何に使用されますか?
統計における範囲の概念を理解するために、それが何に使用されるか、そしてこの分散の尺度をどのように解釈するかを見ていきます。
統計では、範囲はデータセットの最大値と最小値の差を示します。したがって、範囲はデータセットの全体的な分散を示すために使用される尺度です。
データセットの範囲値がわかれば、そのセット内の任意の 2 つの観測値間の最大差がわかるため、データが分散しているか近接しているかを把握できます。一般に、範囲をできるだけ小さくすることが有利です。これは、分散がほとんどなく、計算がより正確になることを意味するためです。
たとえば、この範囲はサンプルの分散を把握できるため、2 つの異なるサンプル間の比較を可能にする測定値になります。
ただし、統計範囲の解釈には誤解を招く可能性があるため注意が必要です。データセットの実際の分散は非常に低い可能性がありますが、サンプル内に外れ値がある場合、範囲が非常に広くなり、サンプルの分散が適切に反映されなくなります。
さらに、値が数十のオーダーであるサンプルがランク 5 を持つことと、値が数千のオーダーであるサンプルが同じランクを持つことは同じではありません。論理的には、両方の範囲の数値が同じであっても、最初のサンプルは 2 番目のサンプルよりもはるかに分散しています。
結論として、範囲はデータセットの分散を分析するための有用な統計的尺度ですが、データを正しく解釈するには、他の指標も計算する必要があります。