Python で自己相関を計算する方法
自己相関は、連続する時間間隔にわたる時系列とそれ自体の時間差バージョンとの間の類似性の度合いを測定します。
変数の現在値とその過去の値の間の関係を測定するため、「逐次相関」または「遅れ相関」と呼ばれることもあります。
時系列における自己相関が高いと、過去の値を参照するだけで将来の値を予測しやすくなります。
Python で自己相関を計算する方法
Python に、15 の異なる期間における特定の変数の値を示す次の時系列があるとします。
#define data
x = [22, 24, 25, 25, 28, 29, 34, 37, 40, 44, 51, 48, 47, 50, 51]
statsmodels ライブラリのacf() 関数を使用して、時系列の各ラグの自己相関を計算できます。
import statsmodels.api as sm #calculate autocorrelations sm.tsa.acf(x) array([ 1. , 0.83174224, 0.65632458, 0.49105012, 0.27863962, 0.03102625, -0.16527446, -0.30369928, -0.40095465, -0.45823389, -0.45047733])
結果を解釈する方法は次のとおりです。
- ラグ 0 での自己相関は1です。
- ラグ 1 での自己相関は0.8317です。
- ラグ 2 での自己相関は0.6563です。
- ラグ 3 での自己相関は0.4910です。
等々。
nlags引数で使用するラグの数を指定することもできます。
sm.tsa.acf(x, nlags= 5 )
array([1.0, 0.83174224, 0.65632458, 0.49105012, 0.27863962, 0.03102625])
Python で自己相関関数をプロットする方法
statsmodels ライブラリのtsaplots.plot_acf() 関数を使用して、Python で時系列の自己相関関数をプロットできます。
from statsmodels.graphics import tsaplots import matplotlib.pyplot as plt #plot autocorrelation function fig = tsaplots.plot_acf(x, lags=10) plt.show()
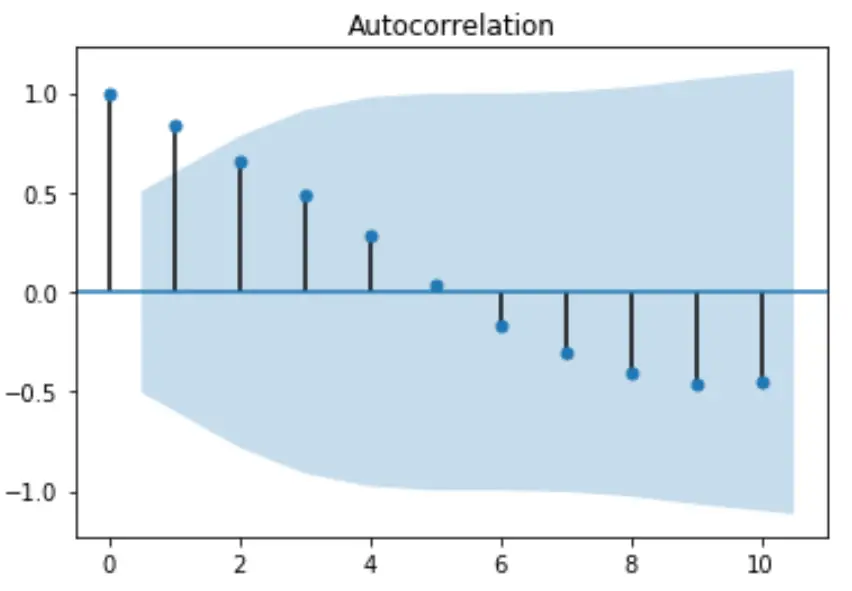
X 軸はラグの数を表示し、Y 軸はそのラグの数での自己相関を表示します。デフォルトでは、プロットはラグ = 0 で開始され、自己相関はラグ = 0 で常に1になります。
lags引数で使用するラグを少なくすることを選択することで、最初のラグにズームインすることもできます。
from statsmodels.graphics import tsaplots import matplotlib.pyplot as plt #plot autocorrelation function fig = tsaplots.plot_acf(x, lags= 5 ) plt.show()
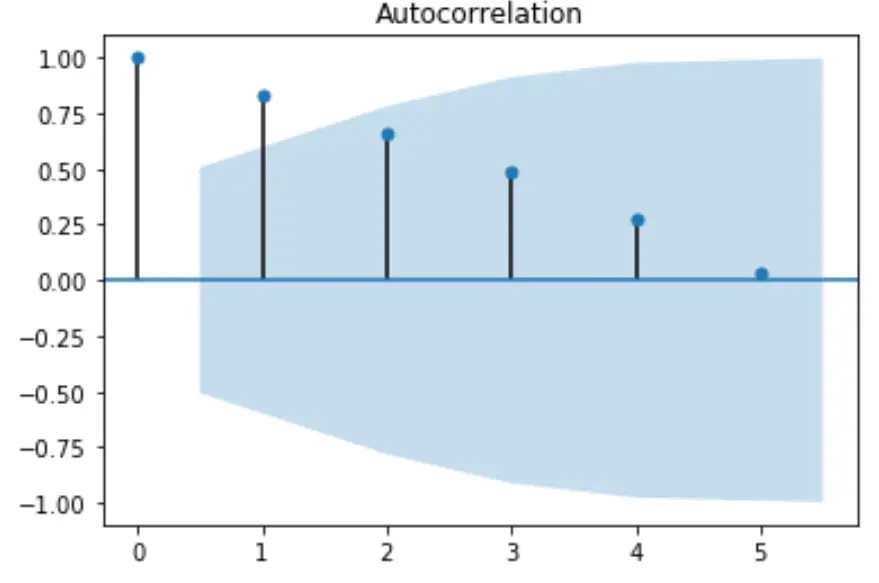
title と color 引数を使用して、プロットで使用される円のタイトルと色を変更することもできます。
from statsmodels.graphics import tsaplots import matplotlib.pyplot as plt #plot autocorrelation function fig = tsaplots.plot_acf(x, lags= 5, color='g', title='Autocorrelation function' ) plt.show()
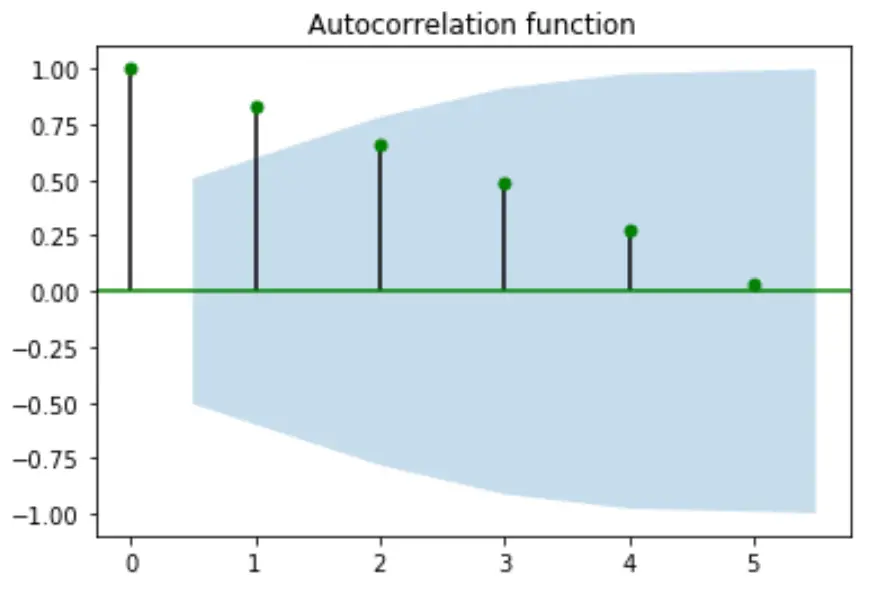
このページでは、その他の Python チュートリアルを見つけることができます。