表から線形回帰式を見つける方法

データの表から線形回帰式を見つけたい場合がよくあります。

たとえば、次のデータテーブルを受け取ったとします。

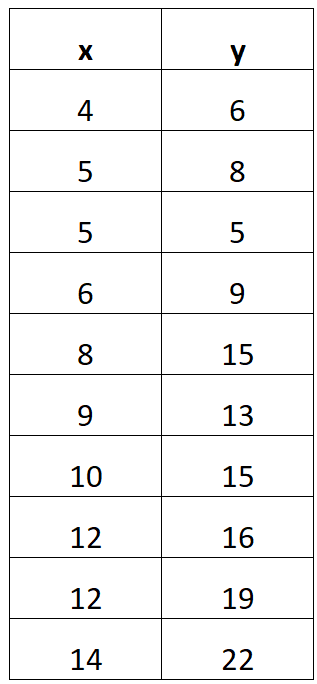
次の段階的な例は、このデータ テーブルから線形回帰式を見つける方法を示しています。

ステップ 1: X*Y、X ²および Y ²を計算する

まず、各行について次のメトリックを計算します。

• x*y
• ^×2
• そして²

次のスクリーンショットは、これを行う方法を示しています。

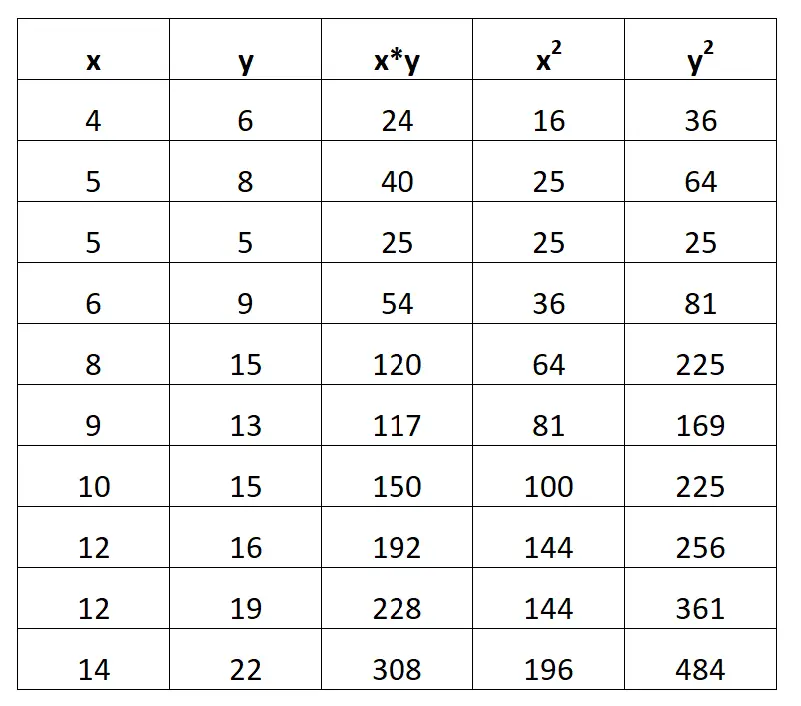
ステップ 2: ΣX、ΣY、ΣX*Y、ΣX ²および ΣY ²を計算します。

次に、各列の合計を計算します。

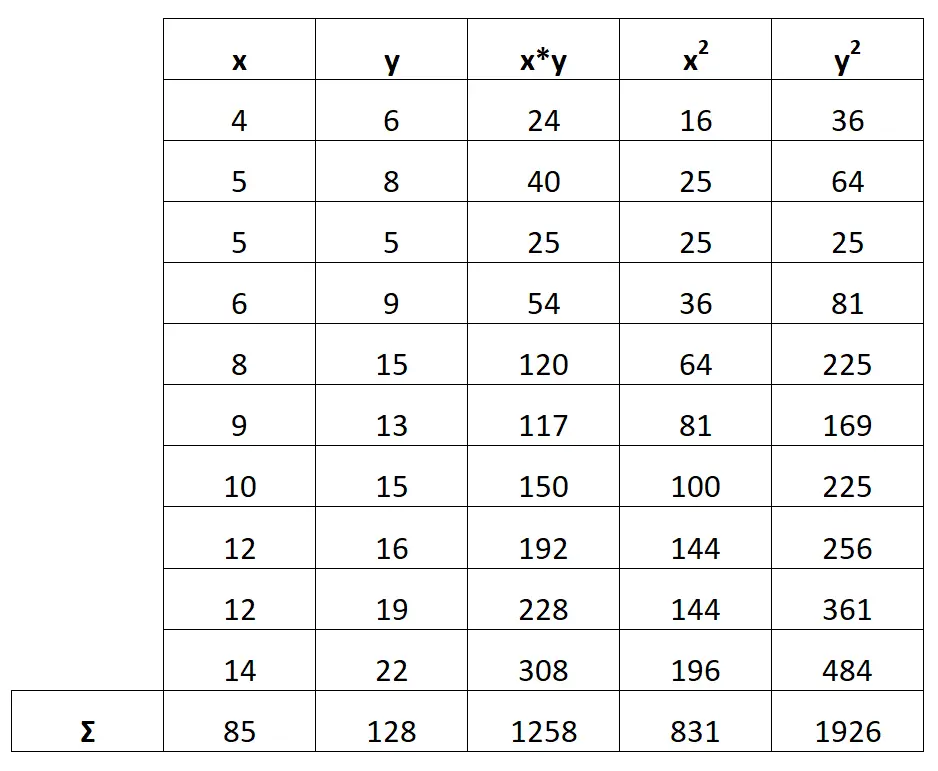
ステップ 3: b ₀を計算する

回帰式の切片 b ₀を計算する式は次のとおりです。

• b ₀ = ((Σy)(Σx ² ) – (Σx)(Σxy)) / (n(Σx ² ) – (Σx) ² )
• b ₀ = ((128)(831) – (85)(1258)) / (10(831) – (85) ² )
• _b0 = -0.518

注: 式中のn は、観測値の総数を表します。この例では、合計 10 個の観測値がありました。

ステップ 4: b ₁を計算する

回帰式の傾き b ₁を計算する式は次のとおりです。

• b ₁ = (n(Σxy) – (Σx)(Σy)) / (n(Σx ² ) – (Σx) ² )
• b ₁ = (10(1258) – (85)(128)) / (10(831) – (85) ² )
• _b1 = 1.5668

ステップ 5: 線形回帰式を書く

最終的な線形回帰式は次のように記述できます。

• ŷ = b ₀ + b ₁ x

したがって、線形回帰方程式は次のように記述されます。

• ŷ = -0.518 + 1.5668x

表の値を単純な線形回帰計算機に代入することで、この答えが正しいことを確認できます。

計算機からの線形回帰式が手動で計算したものと一致していることがわかります。

追加リソース

次のチュートリアルでは、線形回帰に関する追加情報を提供します。

単線形回帰の概要
重線形回帰の概要
回帰係数の解釈方法