Excel で部分 f 検定を実行する方法
部分 F 検定は、回帰モデルと同じモデルのネストされたバージョンの間に統計的に有意な差があるかどうかを判断するために使用されます。
ネストされたモデルは、回帰モデル全体の予測子変数のサブセットを含む単なるモデルです。
たとえば、4 つの予測子変数を含む次の回帰モデルがあるとします。
Y = β 0 + β 1 × 1 + β 2 × 2 + β 3 × 3 + β 4 × 4 + ε
入れ子になったモデルの例は、元の予測子変数が 2 つだけある次のモデルです。
Y = β 0 + β 1 × 1 + β 2 × 2 + ε
これら 2 つのモデルが大きく異なるかどうかを判断するには、部分 F 検定を実行して、次の F 検定統計量を計算します。
F = ((縮小RSS –フルRSS)/p) / (フルRSS /nk)
金：
- Reduced RSS : 縮小された (つまり「ネストされた」) モデルの残差二乗和。
- RSS full : フルモデルの残差二乗和。
- p:完全なモデルから削除された予測子の数。
- n:データセット内の観測値の総数。
- k:完全なモデル内の係数の数 (切片を含む)。
この検定では、次の帰無仮説と対立仮説を使用します。
H 0 :完全なモデルから削除されたすべての係数はゼロです。
H A :完全なモデルから削除された係数の少なくとも 1 つがゼロ以外です。
F 検定統計量に対応するp 値が特定の有意レベル (たとえば、0.05) を下回る場合、帰無仮説を棄却し、完全なモデルから削除された係数の少なくとも 1 つが有意であると結論付けることができます。
次の例は、Excel で部分 F 検定を実行する方法を示しています。
例: Excel での部分 F 検定
Excel に次のデータ セットがあるとします。
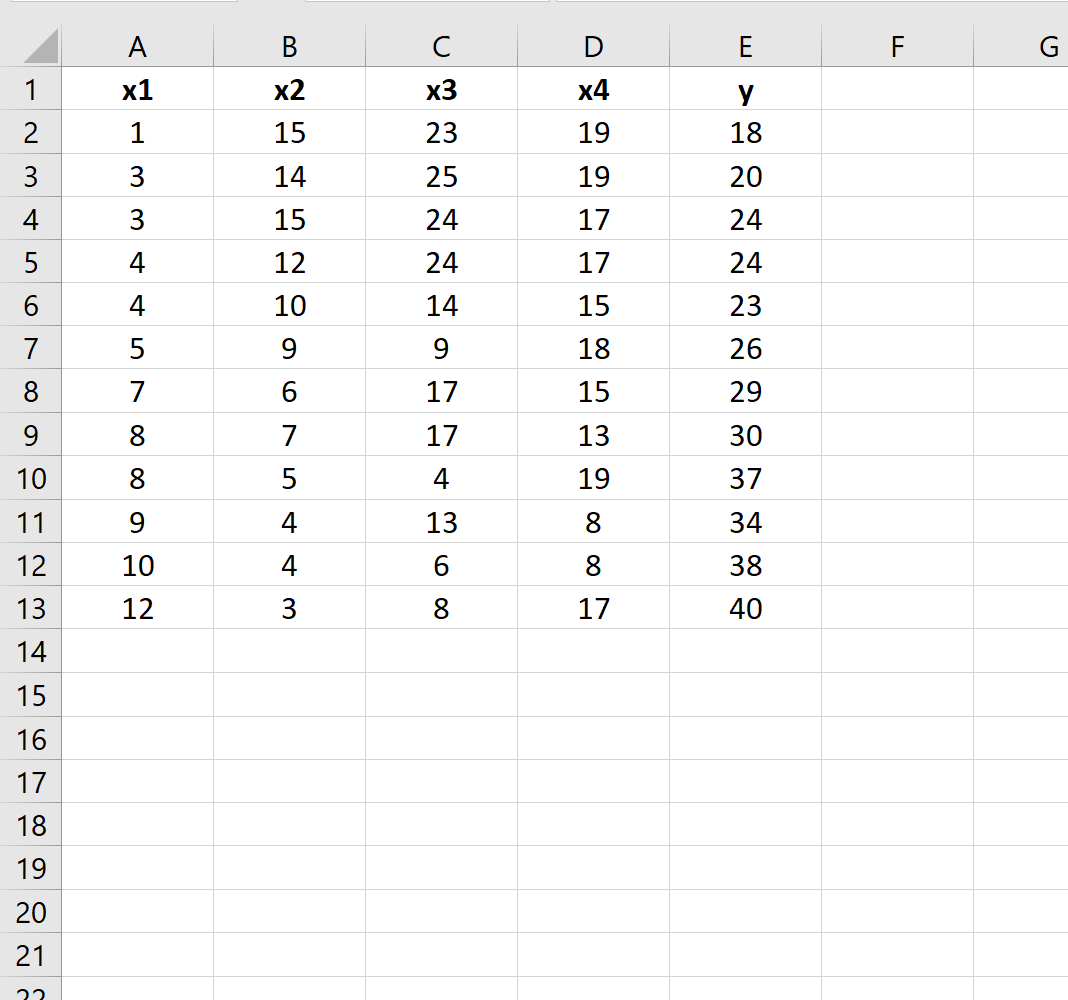
次の 2 つの回帰モデルに違いがあるかどうかを確認したいとします。
完全なモデル: y = β 0 + β 1 x 1 + β 2 x 2 + β 3 x 3 + β 4 x 4
縮小モデル: y = β 0 + β 1 x 1 + β 2 x 2
Excel でモデルごとに重回帰を実行すると、次の結果が得られます。
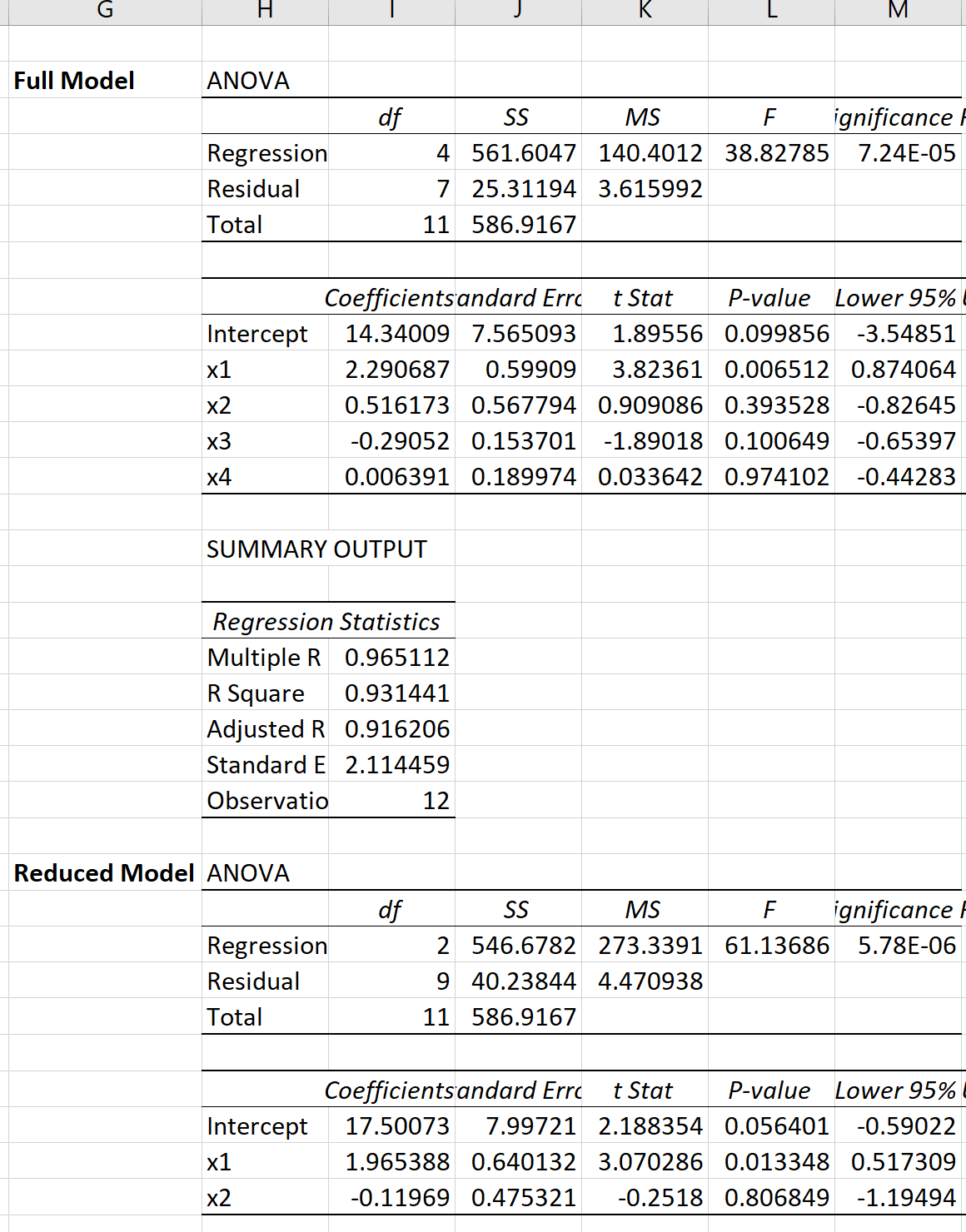
次に、次の式を使用して、部分 F 検定の F 検定統計量を計算できます。
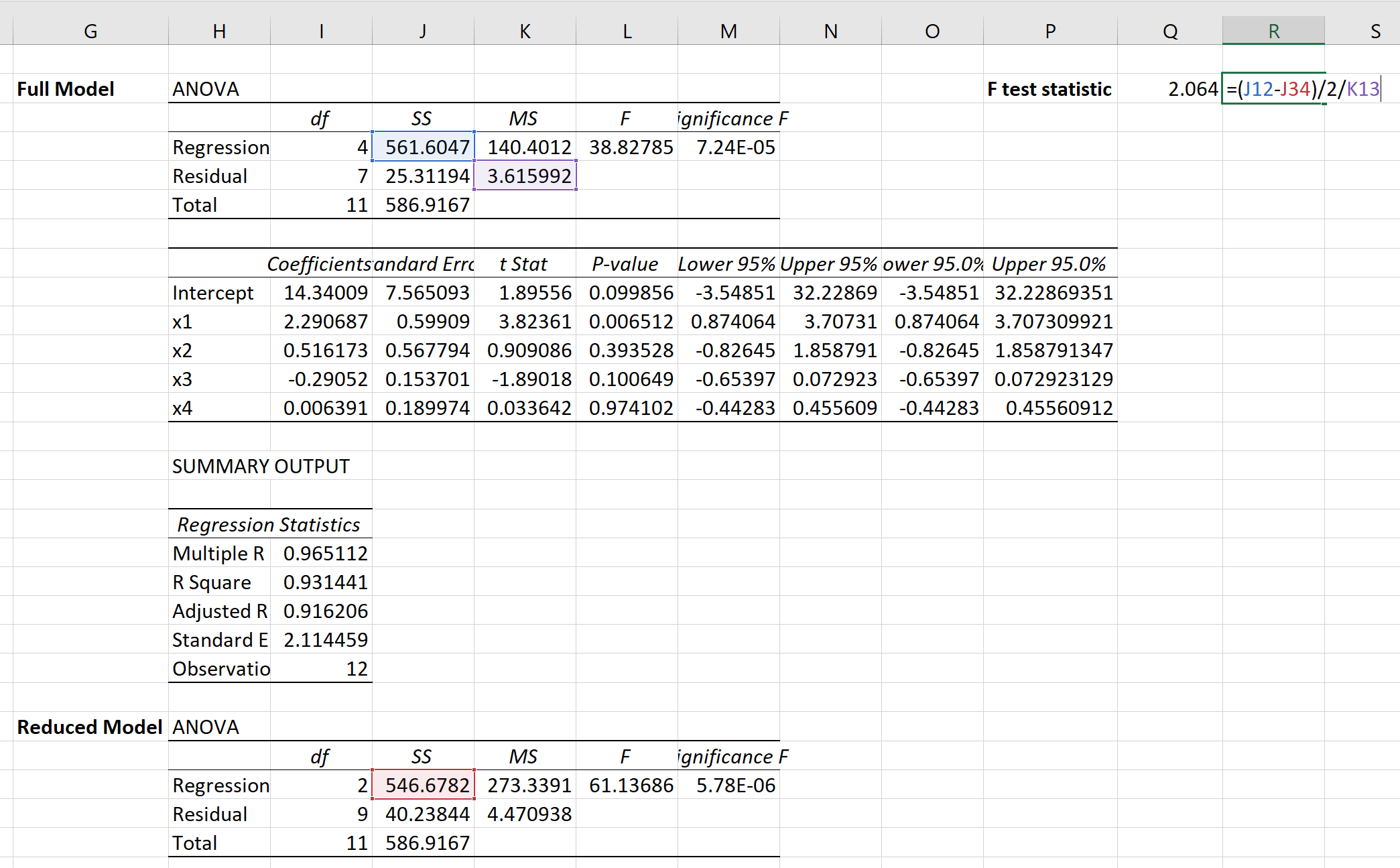
検定統計量は2.064であることがわかります。
次に、次の式を使用して、対応する p 値を計算できます。
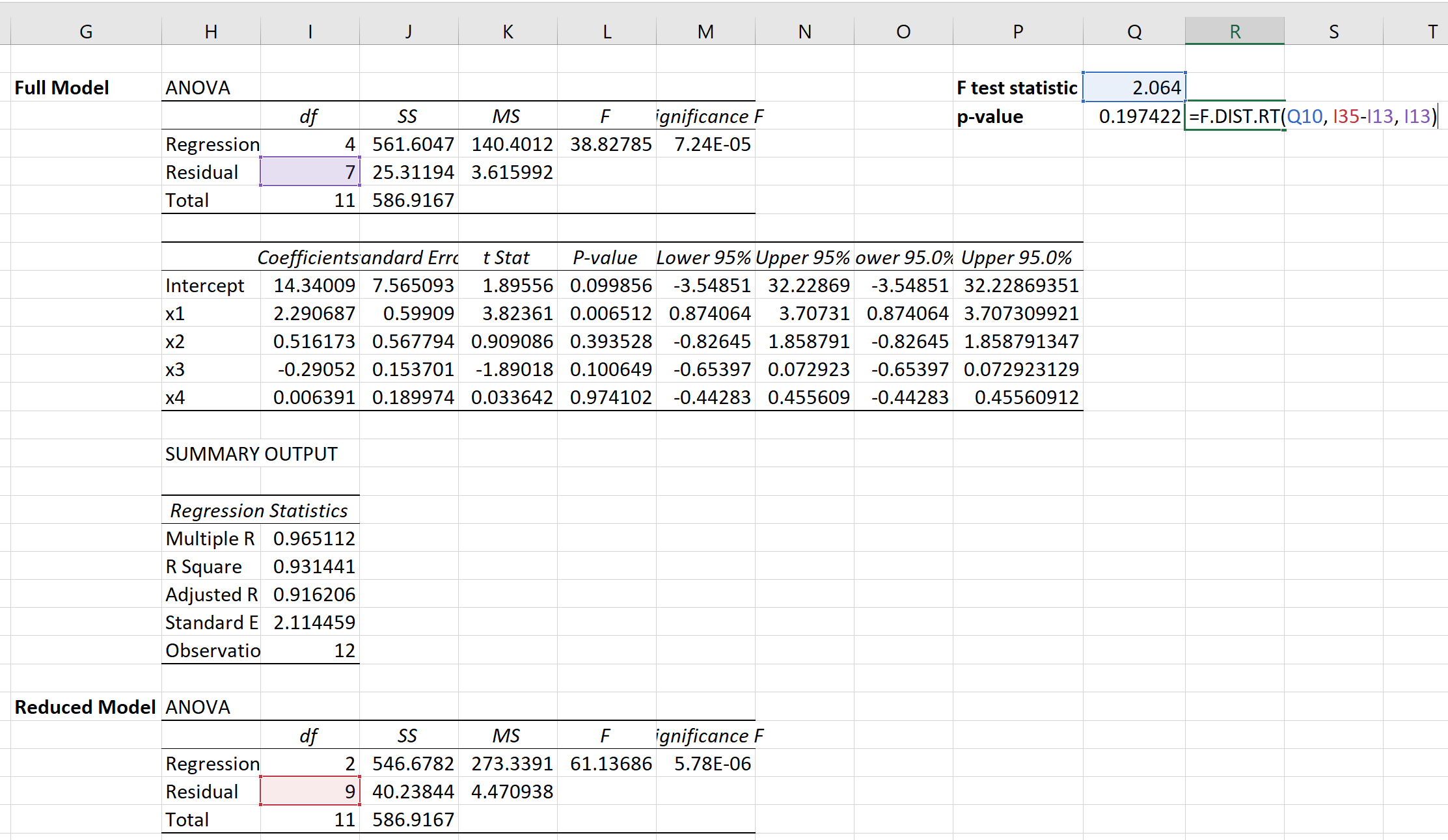
p 値は0.1974であることがわかります。
この p 値は 0.05 未満ではないため、帰無仮説を棄却できません。これは、 x3またはx4予測変数のいずれかが統計的に有意であると言える十分な証拠がないことを意味します。
言い換えれば、 x3とx4 を回帰モデルに追加しても、モデルの適合性は大幅に向上しません。
追加リソース
著者について
ベンジャミン・アンダーソン博士
私はベンジャミンです。退職した統計教授から、専任の Statorials 教育者になりました。 統計分野における豊富な経験と専門知識を活かして、私は Statorials を通じて学生に力を与えるために自分の知識を共有することに尽力しています。もっと知る