統計における非対称性を解釈する方法: 例付き

統計では、分布の対称性を説明するために歪度を使用します。

分布の左側に「裾」がある場合、データ値の分布が歪んでいると言います。

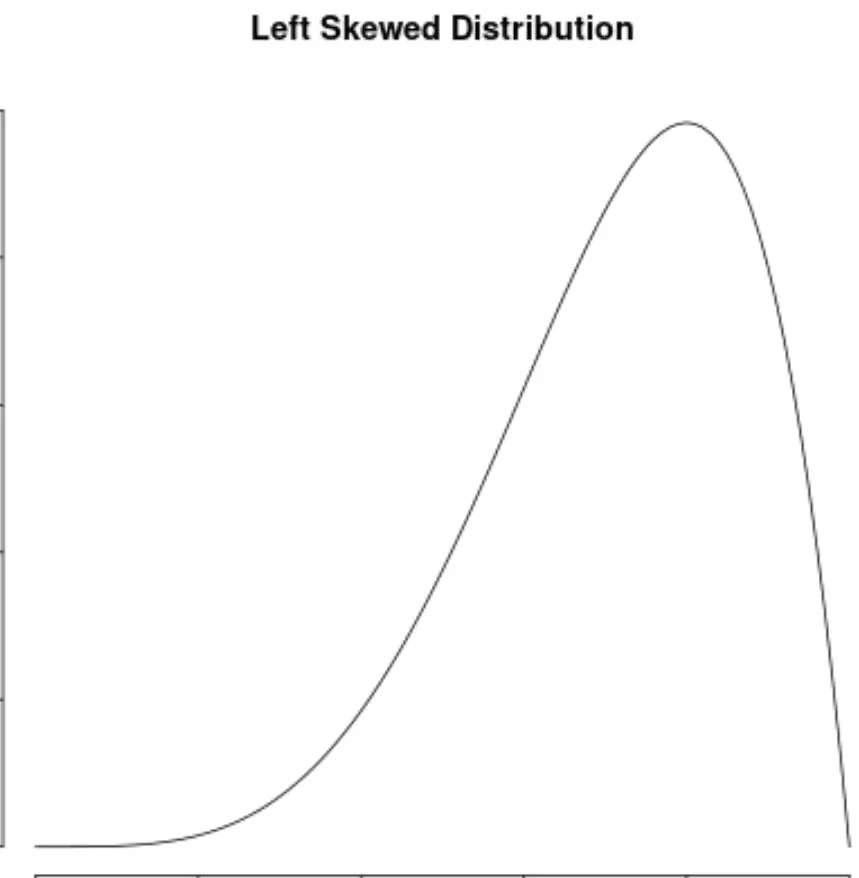
分布の右側に「尾部」がある場合、分布は右に偏っていると言われます。

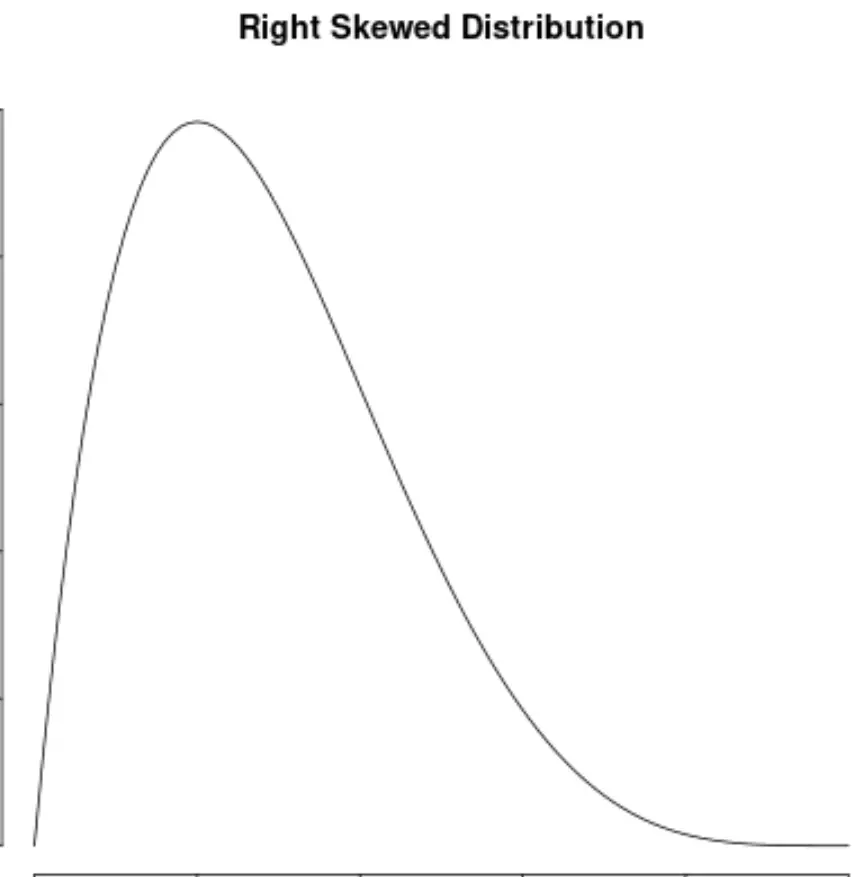
そして、分布が両側で対称であれば、分布には非対称性がないと言います。

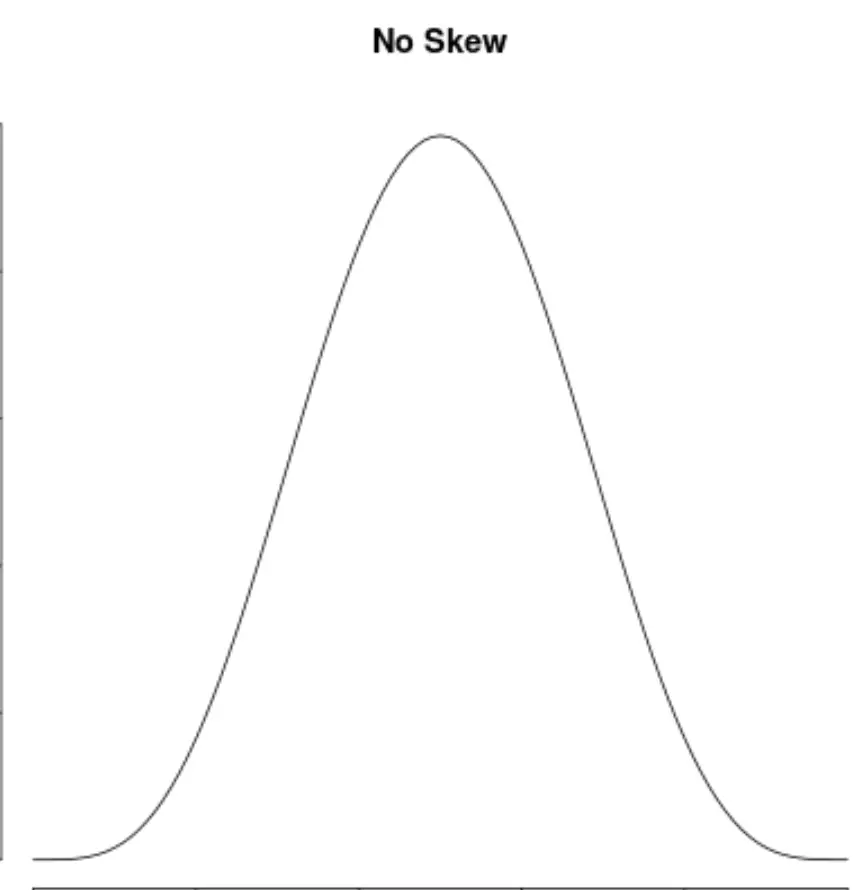
非対称性をどう解釈するか

非対称性の値は、負の無限大から正の無限大までの範囲になります。

非対称値を解釈する方法は次のとおりです。

• 歪度の負の値は、裾が分布の左側にあり、より負の値に向かって広がっていることを示します。
• 歪度の正の値は、裾が分布の右側にあり、より正の値に向かって広がっていることを示します。
• 値 0 は、分布に非対称性がないことを示し、分布が完全に対称であることを意味します。

次の例は、実際に非対称値を解釈する方法を示しています。

例 1: 左に歪んだ分布

ほとんどの人口における死亡者の年齢分布は左に偏っています。ほとんどの人は 70 歳から 80 歳の間で生きますが、この年齢未満で生きる人はますます少なくなります。

死亡年齢の値の分布を視覚化するために密度プロットを作成すると、次のようになります。

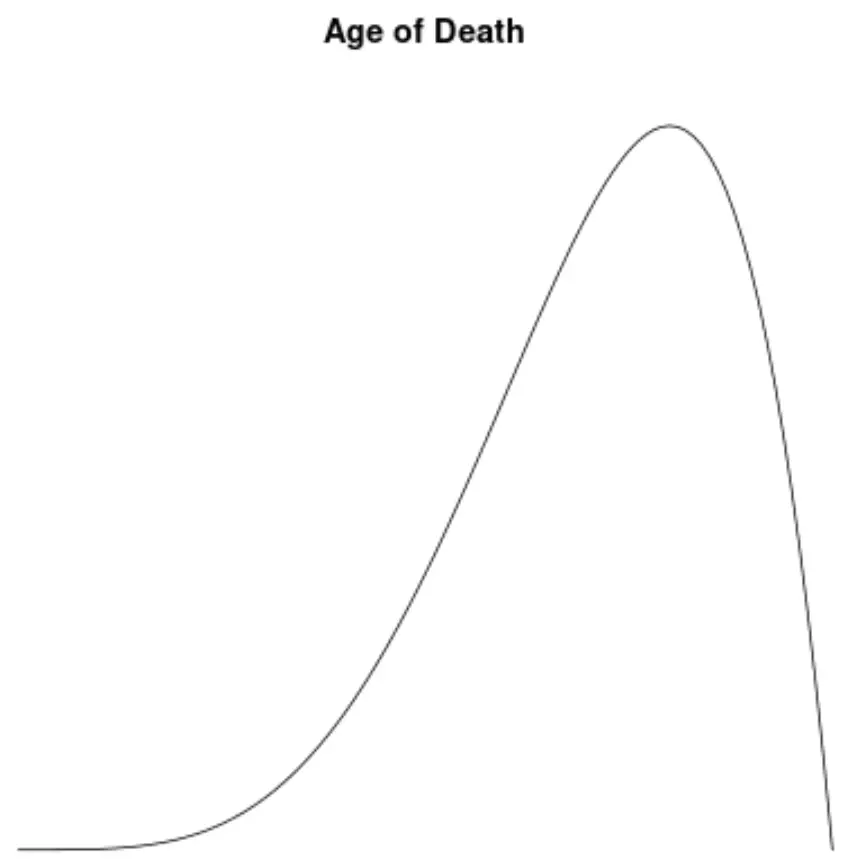
この分布の歪度を計算し、それが-1.3225であることが判明したとします。

この値は負であるため、分布が左に歪んでいること、つまり裾が分布の左側に向かって伸びていることを意味すると解釈します。

例 2: 右に歪んだ分布

米国の世帯収入の分布は右に偏っており、ほとんどの世帯の年間収入は 30,000 ドルから 70,000 ドルですが、右裾の長い世帯ではそれよりも収入が多い世帯もあります。

世帯収入値の分布を視覚化するために密度プロットを作成すると、次のようになります。

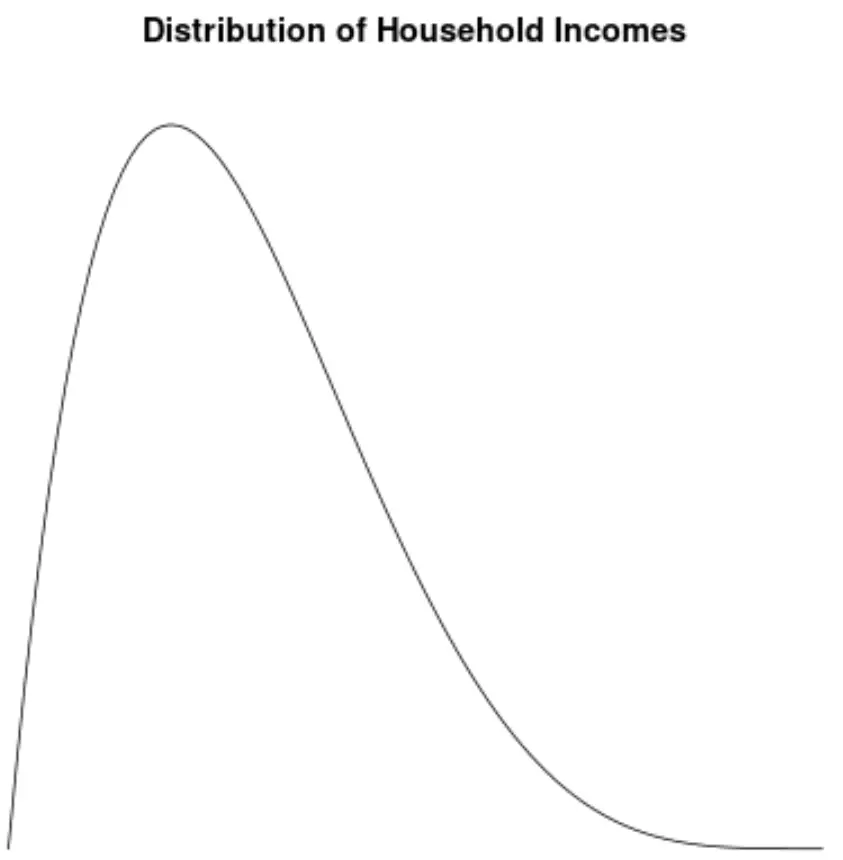
この分布の歪度を計算し、それが2.0043であることが判明したとします。

この値は正であるため、分布が右に歪んでいること、つまり裾が分布の右側に向かって伸びていることを意味すると解釈します。

例 3: バイアスがない

男性のサイズはほぼ正規分布しており、非対称性はありません。たとえば、米国の男性の平均身長は約 69.1 インチです。高さの分布はほぼ対称で、一部は低く、他のものは高くなります。

米国の男性の身長の分布を視覚化するために密度グラフを作成すると、次のようになります。

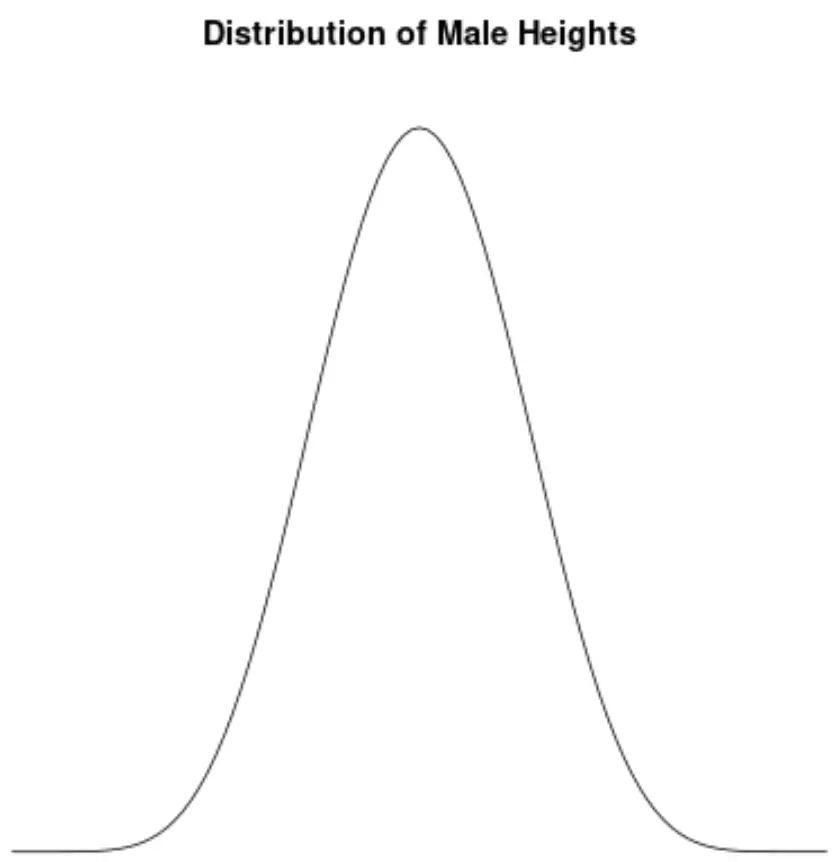
この分布の歪度を計算し、それが0.0013であることが判明したとします。

この値はゼロに近いため、分布に実質的に歪みがないこと、つまり分布の両側の裾がほぼ等しいことを意味すると解釈します。

追加リソース

次のチュートリアルでは、統計の歪みに関する追加情報を提供します。

正に歪んだ分布の 5 つの例
負に歪んだ分布の 5 つの例
Excel で歪度を計算する方法
箱ひげ図で非対称性を特定する方法