Ti-84 計算機でポアソン確率を計算する方法

ポアソン分布は、すべての統計で最もよく使用される分布の 1 つです。このチュートリアルでは、TI-84 計算機で次の関数を使用してポアソン確率を見つける方法について説明します。

Poissonpdf(mean, x) は、ポアソン確率密度関数に関連付けられた確率を返します。

Poissoncdf(mean, x) は、ポアソン cdf に関連付けられた累積確率を返します。

金：

• 平均= 「成功」の平均数
• x = 特定の「成功」数

これら 2 つの関数には、TI-84 電卓で2nd を押してからvarsを押すとアクセスできます。これによりDISTR画面が表示され、そこでFishpdf()とFishcdf()を使用できるようになります。

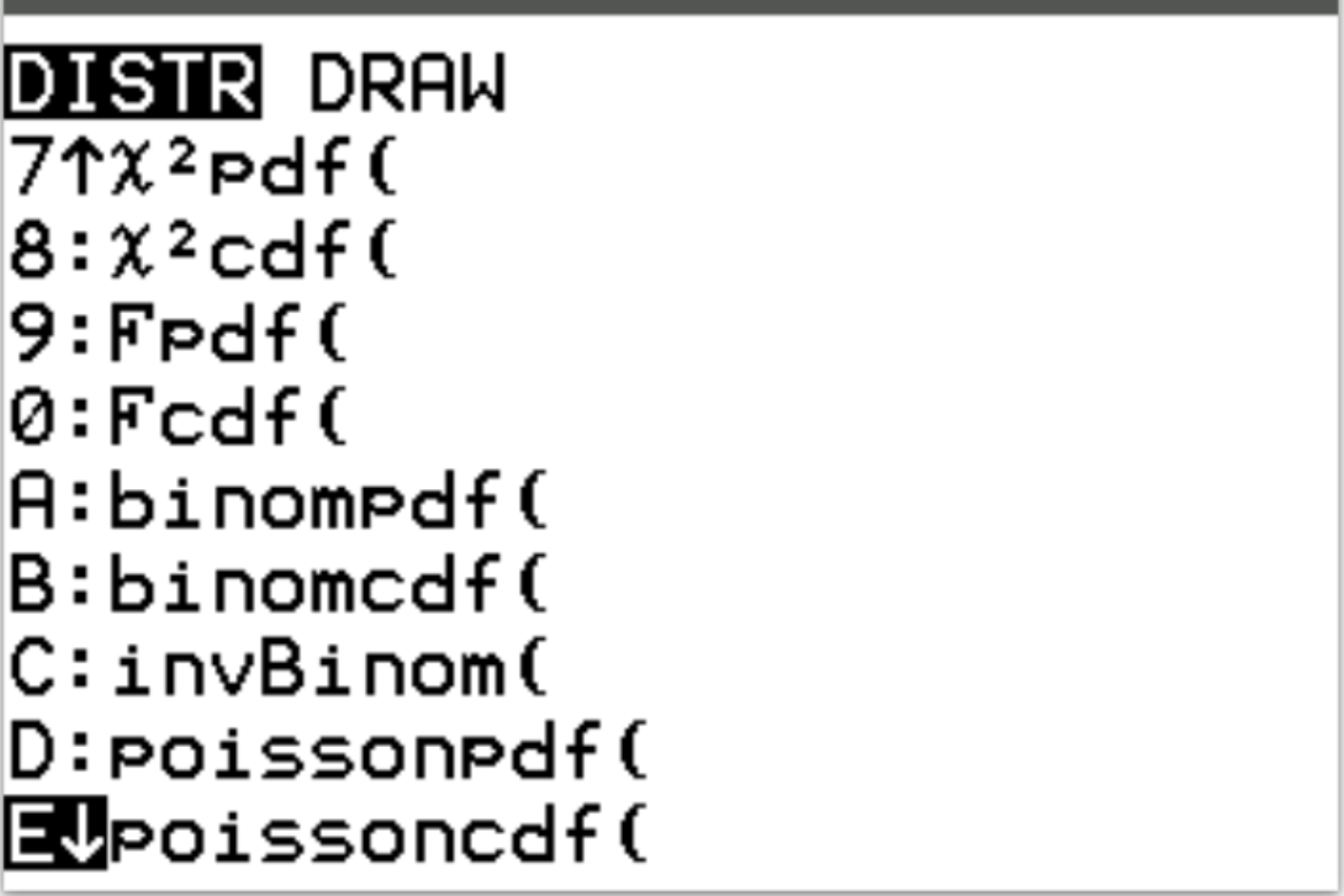
次の例は、これらの関数を使用してさまざまな質問に答える方法を示しています。

例 1: 正確に x が成功するポアソン確率

質問:金物店では 1 日あたり平均 3 個のハンマーが販売されています。特定の日に 5 つのハンマーが売れる確率はどれくらいですか?

答え: Poissonpdf(mean, x) 関数を使用します。

魚pdf(3, 5) = 0.1008

例 2: x 未満の成功のポアソン確率

質問:金物店では 1 日あたり平均 3 個のハンマーが販売されています。特定の日に販売されるハンマーの数が 5 個未満になる確率はどれくらいですか?

答え: Poissoncdf(mean, x-1) 関数を使用します。

フィッシュcdf(3, 4) = 0.8153

例 3: 最大 x 回の成功のポアソン確率

質問:金物店では 1 日あたり平均 3 個のハンマーが販売されています。特定の日に最大 5 個のハンマーが売れる確率はどれくらいですか?

答え: Poissoncdf(mean, x) 関数を使用します。

フィッシュcdf(3, 5) = 0.9161

例 4: x を超える成功のポアソン確率

質問:金物店では 1 日あたり平均 3 個のハンマーが販売されています。特定の日に 5 個以上のハンマーが売れる確率はどれくらいですか?

答え:関数 1 – Poissoncdf(mean, x) を使用します。

1 – フィッシュcdf(3, 5) = 0.0839

例 5: 少なくとも x 回の成功のポアソン確率

質問:金物店では 1 日あたり平均 3 個のハンマーが販売されています。特定の日に少なくとも 5 つのハンマーが売れる確率はどれくらいですか?

答え:関数 1 – Poissoncdf(mean, x-1) を使用します。

1 – フィッシュcdf(3, 4) = 0.1847