サンプルサイズが重要なのはなぜですか? (説明と例)
サンプルサイズとは、実験または研究に関与する人の総数を指します。
サンプルサイズは母集団パラメータの推定精度に直接影響するため、重要です。
この理由を理解するには、信頼区間の基本を理解することが役立ちます。
信頼区間の簡単な説明
統計では、母集団パラメータ、つまり母集団全体の特定の特徴を表す数値を測定しようとすることがよくあります。
たとえば、特定の都市のすべての個人の平均身長を測定したいとします。
ただし、集団内の各個人に関するデータを収集するには、多くの場合、費用と時間がかかりすぎます。したがって、通常は母集団から 無作為に標本を抽出し、その標本データを使用して母集団パラメータを推定します。
たとえば、市内のランダムな 100 人の個人の身長に関するデータを収集できます。次に、サンプル内の個体の平均サイズを計算できます。ただし、サンプルの平均が母集団の平均と正確に一致するかどうかはわかりません。
この不確実性を考慮して、信頼区間を作成できます。信頼区間は、一定の信頼レベルで母集団パラメータが含まれる可能性が高い値の範囲です。
母集団平均の信頼区間を計算する式は次のとおりです。
信頼区間 = x +/- z*(s/√ n )
金:
- x :サンプルの平均値
- z:選択された Z 値
- s:サンプルの標準偏差
- n:サンプルサイズ
使用する Z 値は、選択した信頼レベルによって異なります。次の表は、最も一般的な信頼水準の選択肢に対応する Z 値を示しています。
| 自信のレベル | Z値 |
|---|---|
| 0.90 | 1,645 |
| 0.95 | 1.96 |
| 0.99 | 2.58 |
サンプルサイズと信頼区間の関係
カメの個体群の平均体重を推定したいとします。次の情報を含むカメのサンプルをランダムに収集します。
- サンプルサイズn = 25
- 平均サンプル重量x = 300
- サンプル標準偏差s = 18.5
真の母集団平均体重の 90% 信頼区間を計算する方法は次のとおりです。
90% 信頼区間: 300 +/- 1.645*(18.5/√ 25 ) = [293.91, 306.09]
私たちは、カメの個体群における実際の平均体重が 293.91 ポンドから 306.09 ポンドの間であることを 90% 確信しています。
ここで、25 匹のカメの代わりに 50 匹のカメのデータを収集するとします。
真の母集団平均体重の 90% 信頼区間を計算する方法は次のとおりです。
90% 信頼区間: 300 +/- 1.645*(18.5/√ 50 ) = [295.79, 304.30]
この信頼区間は以前の信頼区間よりも狭いことに注意してください。これは、カメ個体群の真の平均体重の推定値がより正確であることを意味します。
ここで、100 匹のカメのデータを収集するとします。
真の母集団平均体重の 90% 信頼区間を計算する方法は次のとおりです。
90% 信頼区間: 300 +/- 1.645*(18.5/√ 100 ) = [296.96, 303.04]
この信頼区間は、以前の信頼区間よりもさらに狭いことに注意してください。
次の表は、それぞれの信頼区間の幅をまとめたものです。
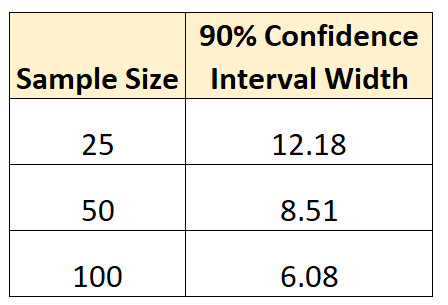
結論は次のとおりです。サンプル サイズが大きいほど、母集団パラメータをより正確に推定できるようになります。
追加リソース
次のチュートリアルでは、信頼区間とサンプルサイズについてさらに役立つ説明を提供します。