Excel でウェルチの t 検定を実行する方法
2 つの独立したグループ間の平均を比較する最も一般的な方法は、2 標本 t 検定を使用することです。ただし、この検定は 2 つのグループ間の分散が等しいことを前提としています。
2 つのグループ間の分散が等しくないと思われる場合は、2 標本 t 検定と同等のノンパラメトリックであるウェルチの t 検定を使用できます。
このチュートリアルでは、Excel でウェルチの t 検定を実行する方法を説明します。
例: Excel でのウェルチの t 検定
この例では、試験準備のために試験準備冊子を使用した 12 人の学生と、試験の準備をしなかった 12 人の学生の結果を比較します。
次の手順に従ってウェルチ t 検定を実行し、2 つのグループ間で試験の平均点に差があるかどうかを判断します。
ステップ 1: データを入力します。
まず、試験結果を 2 つの列に入力します。
ステップ 2: ウェルチの t 検定を実行します。
Excel の上部のリボンで[データ]タブに移動し、 [データ分析]をクリックします。このオプションが表示されない場合は、まず無料の Analysis ToolPak ソフトウェアをインストールする必要があります。

「データ分析」をクリックすると、新しいウィンドウが表示されます。 「t 検定: 不等分散を仮定する 2 つのサンプル」を選択し、 「OK」をクリックします。
新しいウィンドウで、変数 1と変数 2のデータ値の範囲 (グループ ラベルを含む) を入力します。 [Hypothetical Mean Difference]に 0 を入力します。 [Labels]の横のボックスをオンにします。アルファを0.05 に設定したままにします。 [出力範囲]で、テスト結果を表示するセルを選択します。次に、 「OK」をクリックします。
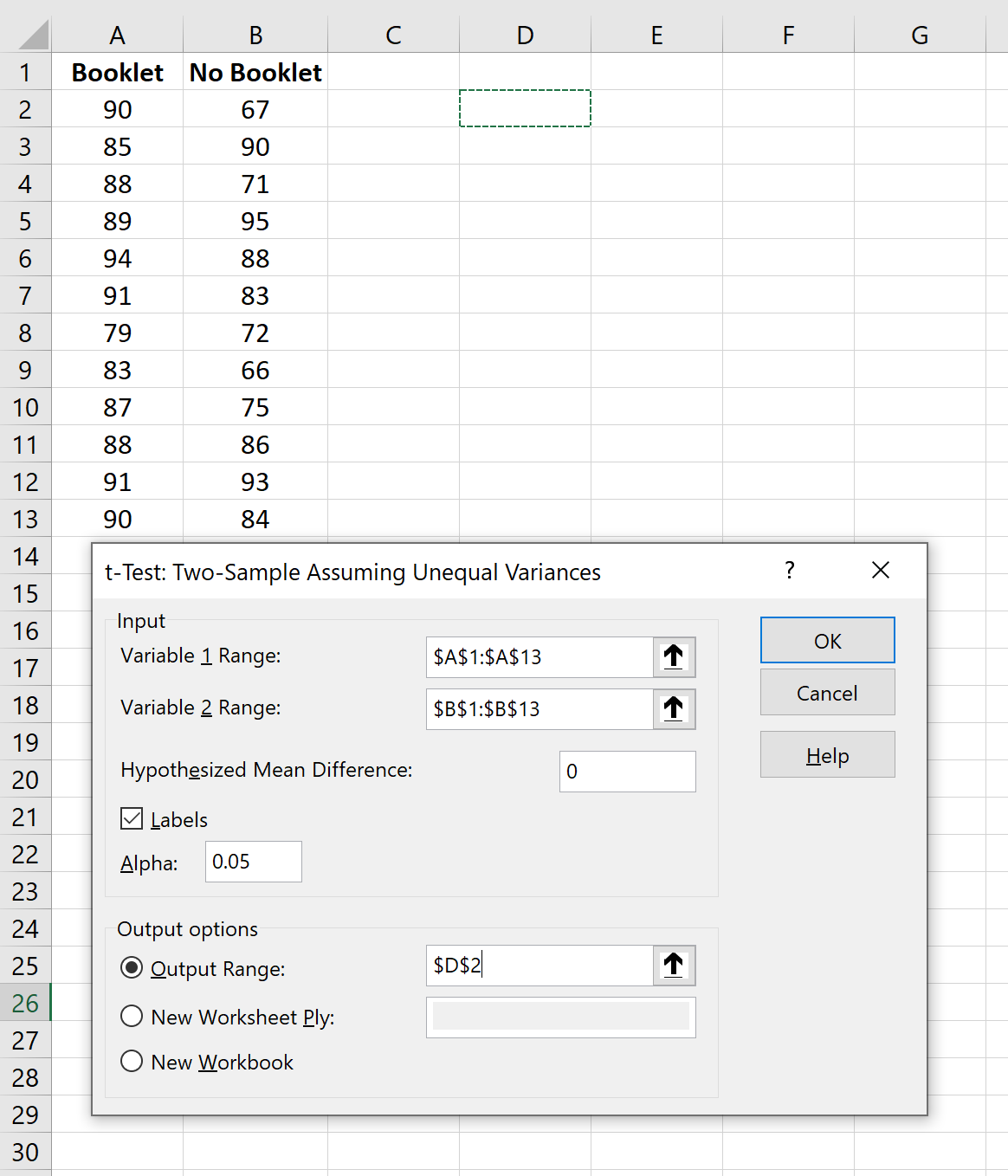
次の出力が自動的に表示されます。
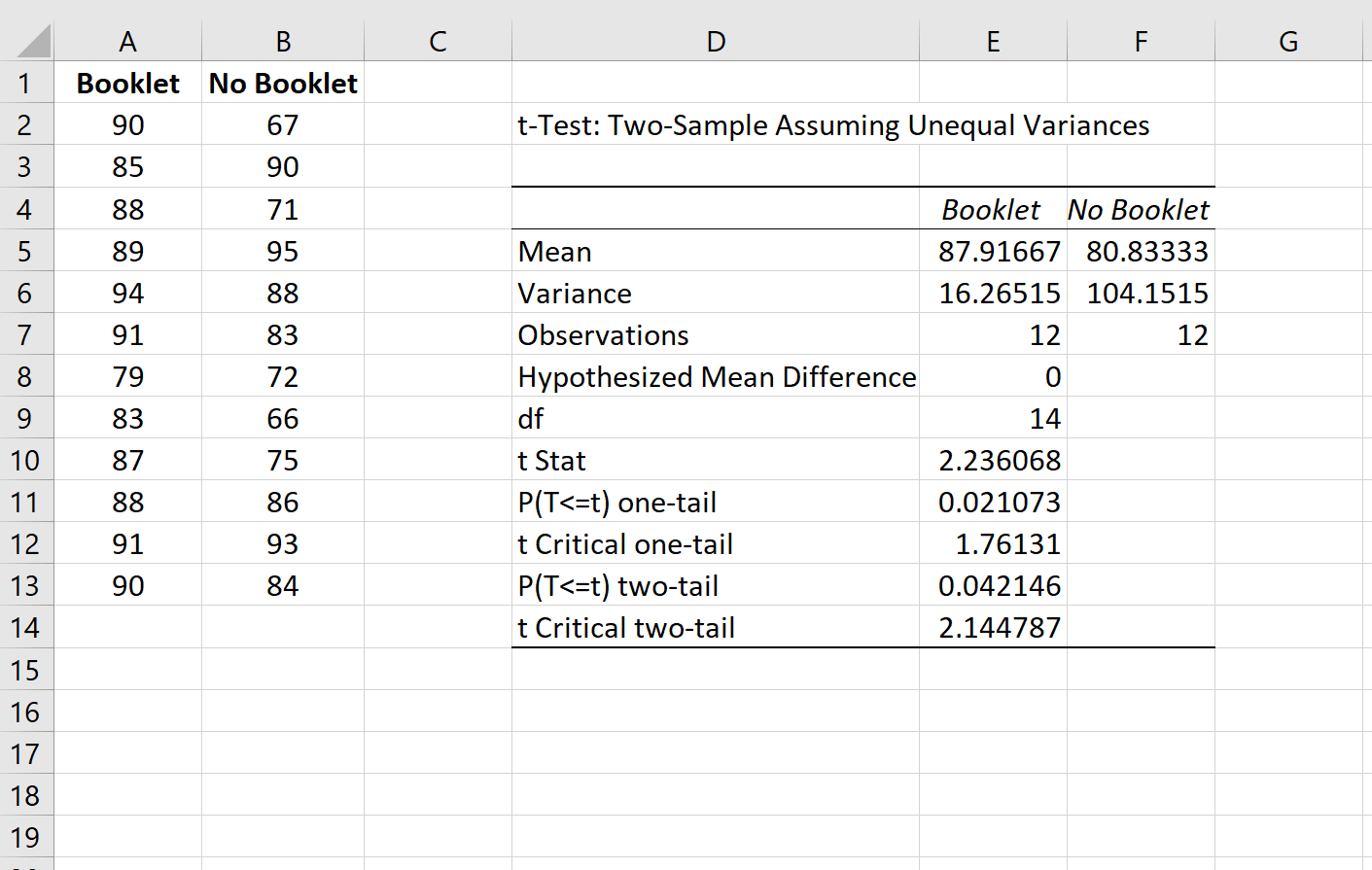
結果を解釈する方法は次のとおりです。
- 平均:各グループの試験の平均点。
- 分散:各グループの試験スコアの分散。
- 観測値:各グループのサンプルサイズ。
- 仮説平均差:検定の帰無仮説で使用する平均差。
- df:検定統計量で使用する自由度。n 1 + n 2 – 2 として計算されます。
- t Stat:テストのテスト統計。
- 片側 P(T<=t):片側検定の検定統計量に関連付けられた p 値。両側検定を実行しているため、これは無視してください。
- P(T<=t) 両側:両側検定の検定統計量に関連付けられた p 値。これは 0.05 未満であるため、帰無仮説は棄却され、2 つのグループ間の平均試験スコアは α = 0.05 レベルで統計的に有意に異なると結論付けられます。
ステップ 3: 結果を報告します。
最後に、Welch の t 検定の結果を報告します。これを行う方法の例を次に示します。
ウェルチの t 検定は、試験の準備に試験対策小冊子を使用した学生のグループと使用しなかった学生のグループとの間で試験のスコアに統計的に有意な差があるかどうかを判断するために実施されました。両方のグループのサンプルサイズは 12 人の学生でした。
ウェルチの t 検定により、2 つのグループ間に平均試験スコア (t=2.236、p=0.0421) に統計的に有意な差があることが明らかになりました。