Sas でロジスティック回帰を実行する方法
ロジスティック回帰は、応答変数がバイナリの場合に回帰モデルを近似するために使用できる方法です。
ロジスティック回帰では、最尤推定として知られる方法を使用して、次の形式の方程式を求めます。
log[p(X) / (1 – p(X))] = β 0 + β 1 X 1 + β 2 X 2 + … + β p
金:
- X j : j番目の予測変数
- β j : j番目の予測変数の係数の推定
方程式の右側の式は、応答変数が値 1 をとる対数オッズを予測します。
次の段階的な例は、SAS でロジスティック回帰モデルを近似する方法を示しています。
ステップ 1: データセットを作成する
まず、18 人の生徒について、次の 3 つの変数に関する情報を含むデータセットを作成します。
- 特定の大学への合格 (1 = はい、0 = いいえ)
- GPA (1 ~ 4 のスケール)
- ACT スコア (1 ~ 36 のスケール)
/*create dataset*/ data my_data; input acceptance gpa act; datalines ; 1 3 30 0 1 21 0 2 26 0 1 24 1 3 29 1 3 34 0 3 31 1 2 29 0 1 21 1 2 21 0 1 15 1 3 32 1 4 31 1 4 29 0 1 24 1 4 29 1 3 21 1 4 34 ; run ; /*view dataset*/ proc print data =my_data;
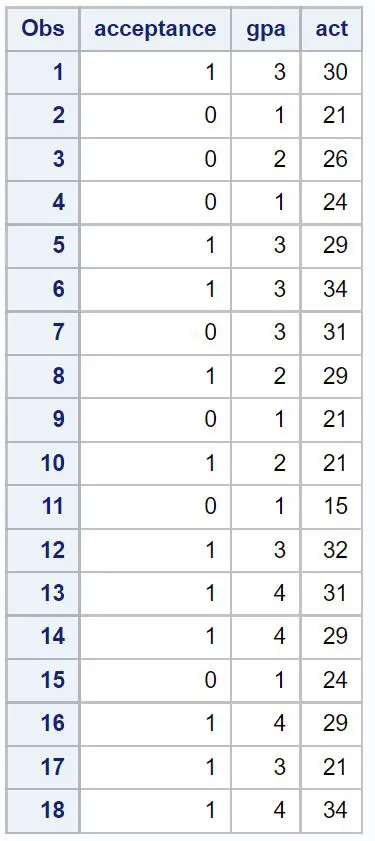
ステップ 2: ロジスティック回帰モデルを当てはめる
次に、 proc ロジスティックスを使用して、応答変数として「acceptance」、予測変数として「gpa」と「act」を使用して、ロジスティック回帰モデルを当てはめます。
注: 応答変数が値 1 をとる確率を予測するには、SAS に減少を指定する必要があります。デフォルトでは、SAS は応答変数が値 0 をとる確率を予測します。
/*fit logistic regression model*/
proc logistic data =my_data descending ;
model acceptance = gpa act;
run ;
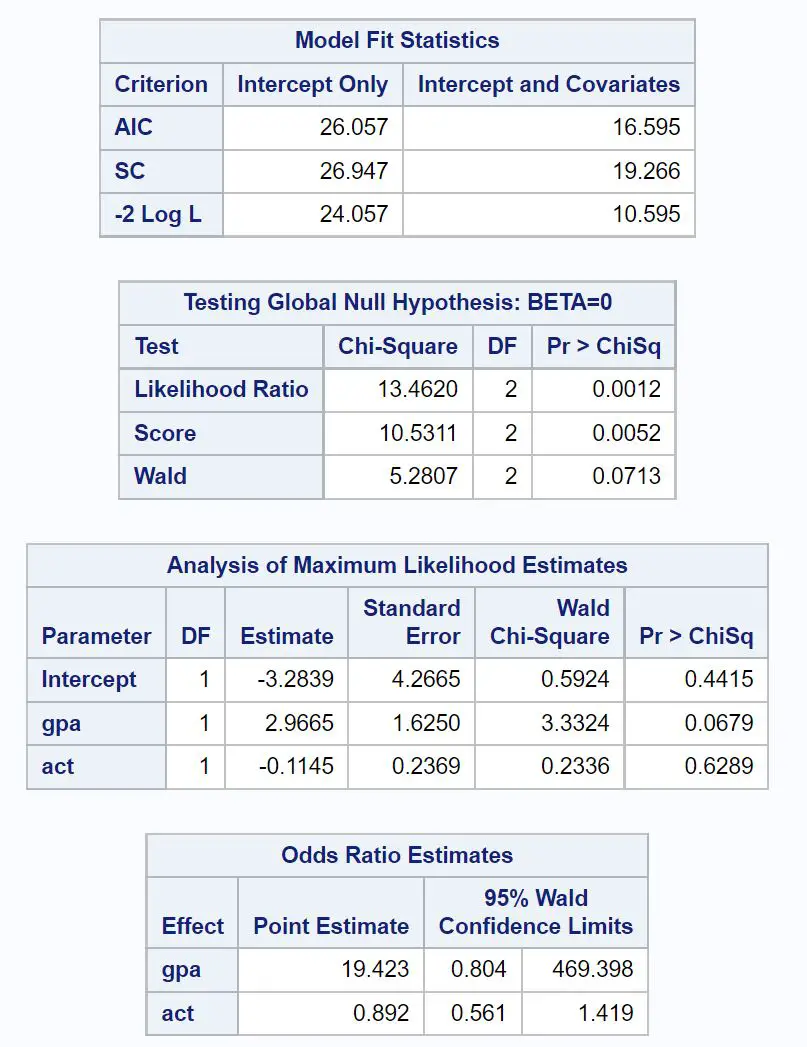
対象となる最初のテーブルのタイトルは、 「Model Fit Statistics」です。
このテーブルから、モデルの AIC 値がわかり、 16.595であることがわかります。 AIC 値が低いほど、モデルはデータに適合しやすくなります。
ただし、 「良好な」 AIC 値とみなされるしきい値はありません。むしろ、AIC を使用して、複数のモデルの同じデータセットへの適合を比較します。一般に、AIC 値が最も低いモデルが最良であると考えられます。
次の興味深いテーブルのタイトルは、「グローバル帰無仮説のテスト: BETA=0」です。
この表から、尤度比のカイ二乗値が13.4620で、対応する p 値が0.0012であることがわかります。
この p 値は 0.05 未満であるため、ロジスティック回帰モデル全体が統計的に有意であることがわかります。
次に、 「 最尤推定値の分析 」というタイトルの表の係数推定値を分析できます。
この表から、gpa と act の係数がわかります。これは、各変数が 1 単位増加した場合の、大学に合格する対数オッズの平均変化を示しています。
例えば:
- GPA 値が 1 単位増加すると、大学に合格する対数オッズが平均2.9665増加します。
- ACT スコアが 1 単位増加すると、大学に合格する対数オッズが平均0.1145減少します。
結果の対応する p 値からも、各予測変数が受け入れられる可能性を予測する際にどの程度効果的であるかがわかります。
- GPA P 値: 0.0679
- ACT P 値: 0.6289
これは、GPA が大学合格の統計的に有意な予測因子であるように見える一方で、ACT スコアは統計的に有意ではないようであることを示しています。
追加リソース
次のチュートリアルでは、SAS で他の回帰モデルを適合させる方法について説明します。