ガンマ分布
この記事では、ガンマ分布とは何か、またその用途について説明します。したがって、ガンマ分布の定義、そのプロパティ、およびそのグラフィック表現がどのようなものであるかがわかります。
ガンマ分布とは何ですか?
ガンマ分布は、 2 つの特性パラメータ α と λ によって定義される連続確率分布です。言い換えれば、ガンマ分布は 2 つのパラメータの値に依存します。α は形状パラメータ、λ はスケール パラメータです。
ガンマ分布の記号はギリシャ文字の大文字 Γ です。したがって、確率変数がガンマ分布に従う場合、次のように記述されます。
![]()
ガンマ分布は、形状パラメーター k = α と逆スケール パラメーター θ = 1/λ を使用してパラメーター化することもできます。すべての場合において、ガンマ分布を定義する 2 つのパラメーターは正の実数です。
通常、ガンマ分布は右に歪んだデータセットをモデル化するために使用されるため、グラフの左側にデータが集中します。たとえば、ガンマ分布は電気コンポーネントの信頼性をモデル化するために使用されます。
ガンマ分布図
ガンマ分布のグラフは、その特性パラメータの値に依存します。以下に、ガンマ分布の密度関数が形状パラメーターとスケール パラメーターに応じてどのように変化するかを示します。
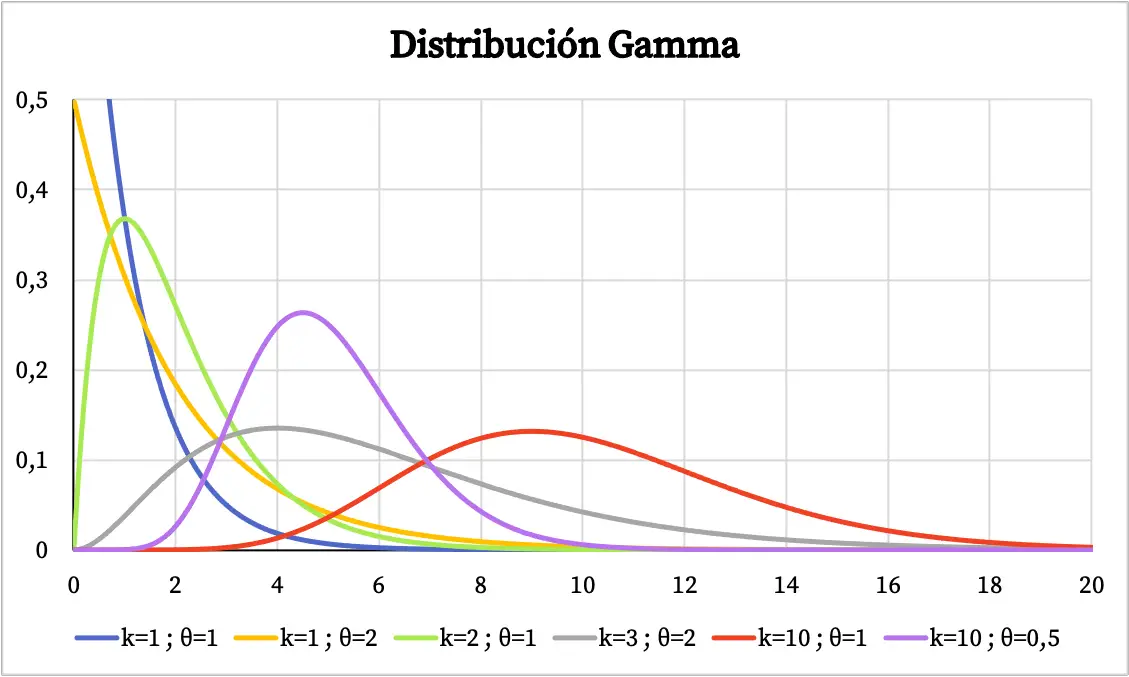
一方、ガンマ分布の累積確率関数のグラフを以下に示します。
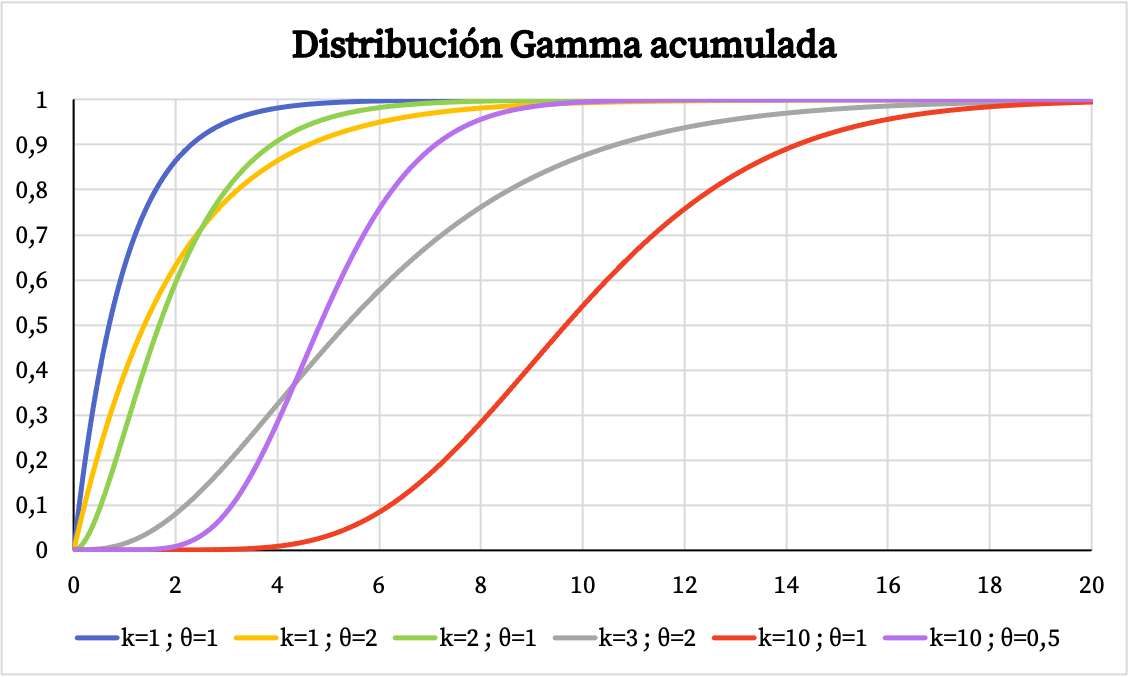
ガンマ分布の特徴
次に、ガンマ分布の特徴がどのようなものであるかを見ていきます。
- ガンマ分布のグラフは、その 2 つの特性パラメーターによって完全に定義されます。α は形状パラメーター、λ はスケール パラメーターです。
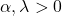
![]()
- ガンマ分布の平均は、形状パラメータとスケール パラメータの比、つまり α/λ に等しくなります。
![]()
- ガンマ分布の分散は、形状パラメーターをスケール パラメーターの 2 乗で割ったものに相当します。
![]()
- α の値が 1 未満の場合、最頻値は 0 です。ただし、α が 1 以上の場合、ガンマ分布の最頻値は次の式で計算できます。
![Rendered by QuickLaTeX.com \begin{array}{c}Mo=0 \qquad \text{para } \alpha<1\\[2ex]Mo=\cfrac{\alpha-1}{\lambda} \qquad \text{para } \alpha\geq1\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-c9e2762af62f9c38870902ec0284ee07_l3.png)
- ガンマ分布の密度関数の式は次のとおりです。
![]()
ここで、Γ はガンマ関数であり、次のように定義されます。
![]()
- ガンマ分布によって定義される確率変数の累積分布の式は次のとおりです。
![]()
- 形状パラメータ α が 1 に等しい場合、ガンマ分布は同じスケール パラメータ λ を持つ指数分布と等価です。
![]()
- スケール パラメーター λ が平均の場合、ガンマ分布はカイ二乗分布の特殊なケースになります。
![]()