割合の標本分布

によるベンジャミン・アンダーソン博士 8月 3, 2023 統計 0コメント

この記事では、統計における割合の標本分布とは何かについて説明します。同様に、比例サンプリング分布の公式と、さらにステップバイステップで解決する練習問題も表示されます。

割合の標本分布はどうなるでしょうか?

割合の標本分布(または割合の標本分布) は、母集団から考えられる各サンプルの割合を計算して得られる分布です。つまり、母集団から得られるすべてのサンプルの標本比率が、その比率の標本分布を形成します。

言い換えれば、比率の標本分布は、母集団から選択できるすべてのサンプルを調査し、各サンプルの標本比率を導出することによって得られます。したがって、計算されたサンプル比率のセットは、比率のサンプル分布を構成します。

比率の標本分布が何のためにあるのか疑問に思っている場合は、統計では、単一のサンプルを分析するときに母集団の比率の値に近づく確率を計算するために使用されます。

➤参照:平均値の標本分布

比例サンプリング分布式

実際、サンプルの一部を調査するときは、成功事例を分析します。したがって、研究の確率変数は二項確率分布に従います。

中心極限定理によれば、大きなサイズ (n>30) の場合、二項分布を正規分布に近づけることができます。したがって、比率の標本分布は、次のパラメーターを使用して正規分布に近似します。

$\begin{array}{c}\displaystyle\mu_{p}=p \qquad \sigma_{p}=\sqrt{\frac{pq}{n}}\\[4ex]\displaystyle N_{p}\left(p, \sqrt{\frac{pq}{n}}\right) \end{array}$

金

$p$

は成功の確率であり、

$q$

失敗の確率です

$q=1-p$

。

注:二項分布は、次の場合にのみ正規分布に近似できます。

$n>30″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”52″ style=”vertical-align: -2px;”> 、 <p class=$ $np\ge 5$

そして

$nq\ge 5$

。

➤参照:正規分布の例

したがって、割合の標本分布は正規分布に近似できるため、標本の割合に関連する確率を計算する式は次のようになります。

$Z=\cfrac{\widehat{p}-p}{\displaystyle\sqrt{\frac{pq}{n}}}$

金：

$\widehat{p}$

はサンプルの割合です。
$p$

人口に占める割合です。
$q$

は母集団が失敗する確率であり、

$q=1-p$

。
$n$

はサンプルサイズです。
$Z$

は、標準正規分布 N(0,1) によって定義される変数です。

比例抽出分布の具体例

比例標本分布の定義とそれに関連する式が何であるかを理解したら、概念を完全に理解するために、段階的に解決した例を以下に示します。

ある産業会社は、欠陥部品が 3% しか含まれていない部品を製造していると主張する工場から部品のバッチを購入します。これを確認するために、同社は 500 個の部品の注文を分析することにしました。サンプル内で 5% を超える欠陥部品が見つかる確率はどれくらいですか?

この場合、調査したい母集団の割合は 0.03 であるため、パラメーター q は 0.97 に相当します。

$\begin{array}{c}p=0,03\\[2ex]q=1-p=0,97\end{array}$

したがって、彼らが尋ねる確率を見つけるには、前のセクションで見た式を適用して、対応する統計を計算する必要があります。

$Z=\cfrac{\widehat{p}-p}{\displaystyle\sqrt{\frac{pq}{n}}}=\cfrac{0,05-0,03}{\displaystyle\sqrt{\frac{0,03\cdot 0,97}{500}}}=2,62$

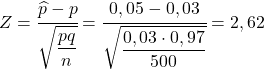
したがって、5% を超える不良部品が発生する確率は、次の確率に相当します。

$P\left[\widehat{p}>0,05\right]=P[Z>2,62]=1-P[Z\leq 2,62]” title=”Rendered by QuickLaTeX.com” height=”19″ width=”360″ style=”vertical-align: -5px;”> 最後に、 <a href=$ Z 分布表で P[Z≤2.62] の確率を探し、問題が求める確率を計算します。

$\begin{array}{l}P\left[\widehat{p}>0,05\right]=\\[2ex]=P[Z>2,62]=\\[2ex]=1-P[Z\leq 2,62]=\\[2ex]=1-0,9956=\\[2ex]=0,0044\end{array}” title=”Rendered by QuickLaTeX.com” height=”167″ width=”162″ style=”vertical-align: 0px;”> 結論として、分析されたサンプルで 5% 以上の欠陥部品が見つかる確率は 0.44% です。 </div>  <div class=$

著者について

ベンジャミン・アンダーソン博士

私はベンジャミンです。退職した統計教授から、専任の Statorials 教育者になりました。統計分野における豊富な経験と専門知識を活かして、私は Statorials を通じて学生に力を与えるために自分の知識を共有することに尽力しています。もっと知る

割合の標本分布はどうなるでしょうか?

比例サンプリング分布式

比例抽出分布の具体例

著者について

ベンジャミン・アンダーソン博士

コメントを追加する