サンプルサイズ
この記事では、サンプルサイズとは何か、そしてそれが統計においてなぜ重要なのかについて説明します。さらに、適切なサンプルサイズを計算する方法と、それがどのように行われるかを確認できるように解決された演習を確認します。
サンプルサイズはどれくらいですか?
サンプル サイズ(またはサンプル サイズ) は、研究のサンプルを構成する個人の数です。統計では、サンプルが母集団全体を代表するようにサンプル サイズが重要です。
したがって、統計研究のサンプルサイズは、母集団全体の特性を表すのに十分な大きさでなければなりません。一方で、研究の費用が高くなるため、サンプルサイズを過度に大きくすることはできません。結論として、サンプル サイズは大きすぎても小さすぎてもならず、適切である必要があります。
たとえば、国の標高を分析したい場合、その国の全住民の身長を尋ねることはできません。調査には時間がかかり、費用もかかりすぎるからです。したがって、無作為抽出を実施し、母集団の代表的なサンプルのみにインタビューする必要があります。
そして、適切なサンプルサイズはどうやって知ることができるのでしょうか?次のセクションでは、調査要件に基づいて適切なサンプル サイズを決定する方法を見ていきます。
サンプルサイズの計算方法
平均値を推定するために必要なサンプル サイズは、Z の 2 乗α/2に標準偏差 (σ) を乗算し、必要な誤差の範囲 (e) で除算したものに等しくなります。したがって、サンプルサイズを計算する式は次のようになります。
![]()
金:
-

はサンプルサイズです。
-
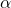
望ましい重要度レベルです。これを考慮すると
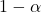
は望ましい信頼レベルです。
-

α/2 の確率に対応する標準正規分布の分位数です。サンプルサイズが大きく、95% の信頼水準の場合は通常 1.96 に近く、99% の信頼水準の場合は通常 2.576 に近くなります。
-

は標準偏差です。
この式では、母集団のサイズが無限である、つまり母集団のサイズが非常に大きいか未知であると想定されていることに注意してください。
注:上の式は、平均の信頼式区間から導出されています。
サンプルサイズの計算例
このセクションでは、例として統計調査に適したサンプル サイズを計算します。
- 母集団の標準偏差が約 15 であることはわかっていますが、その平均値はわからないため、平均値を推定する研究を実行したいと考えています。信頼水準 95% で誤差範囲 ±2 が必要な場合、サンプル サイズはどれくらい必要ですか?
上で見たように、サンプル サイズを計算する式は次のとおりです。
![]()
この場合、望ましい信頼水準は 95% であるため、対応する Z α/2値は 1.96 になります。
![]()
![Rendered by QuickLaTeX.com \begin{array}{c}Z_{\alpha/2}= \ \color{orange}\bm{?}\\[4ex]Z_{0,025}=1,96\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-54dda39d0da5b29f2d25728b89565859_l3.png)
最後に、すべてのパラメーターの価値がわかったので、それらの値を式に代入してサンプル サイズを計算します。
![Rendered by QuickLaTeX.com \begin{aligned}\displaystyle n&=\left(\frac{Z_{\alpha/2}\cdot\sigma}{e}\right)^2\\[2ex] n&=\left(\frac{1,96\cdot 15}{2}\right)^2\\[2ex] n&=216,09 \approx 217 \end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-dd8e2d30042f759051fb52c5c55ade44_l3.png)
つまり、望ましい要件で母集団平均を推定するには、少なくとも 217 人のサンプルが必要です。
サンプルサイズ、信頼水準、誤差の範囲
必要な信頼レベルと許容誤差に応じて、必要なサンプル サイズは異なります。したがって、サンプルサイズ、信頼水準、誤差範囲は次のように関係します。
- サンプルサイズと信頼水準は正比例します。つまり、信頼水準が増加すると、サンプルサイズも増加します。
- サンプルサイズと誤差の範囲は反比例します。したがって、誤差の範囲が増加すると、サンプルサイズは減少します。
- したがって、サンプルサイズを増やすと、信頼水準が向上したり、誤差の範囲が減少したりする可能性があります。
その他のサンプルサイズの計算式
推定するパラメータに応じて、必要なサンプル サイズの計算式は若干異なります。したがって、このセクションでは、いくつかの特殊なケースでサンプル サイズを計算するのに役立つ他の式を見ていきます。
割合のサンプルサイズ
割合 (p) を推定するために必要なサンプル サイズを計算する式は次のとおりです。
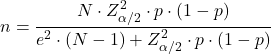
確率のサンプルサイズ
確率を推定する場合は、次の式を使用して必要なサンプル サイズを決定することをお勧めします。
![]()
2 つの独立した平均値を比較するためのサンプル サイズ
与えられた α リスクおよび β リスクで 2 つの独立した平均を比較する場合のサンプル サイズを計算する式は次のとおりです。
![]()
金
![]()
対立仮説の 2 つの平均の差です。
2つの一対の平均を比較するためのサンプルサイズ
固定誤差 α と誤差 β を持つ 2 つの一対の平均を比較する場合、サンプル内の観測値の数を見つけるために使用する式は次のとおりです。
![]()
金
![]()
対立仮説の 2 つの一対の平均の差です。
![]()
これは、同じ個人の 2 つの測定値間の差の分散です。