スタージェスの法則
この記事では、スタージェスの法則とは何か、そしてその公式は何であるかを説明します。また、スタージェス ルールの段階的な具体例と、オンラインのスタージェス ルール計算ツールも見つかります。
スタージェスの法則とは何ですか?
スタージェスの法則は、データセットを分割する理想的なクラス数または間隔を計算するために使用されるルールです。
スタージェスの法則の公式では、クラスの数は 1 にデータの総数の底 2 の対数を加えたものに等しいと規定されています。
![]()
金
![]()
はクラスまたはインターバルの数、および
![]()
サンプル内の観測値の合計数です。
ほとんどの電卓では、10 を底とする対数での計算のみが可能です。この場合、次の同等の式を使用できます。
![]()
スタージェス ルールは、1926 年にドイツの統計学者ヘルベルト スタージェスによって作成されました。
スタージェス則の例
スタージェス則が何であるかがわかったので、段階的な演習を解いて、統計でスタージェス則を使用してデータセットの間隔がどのように計算されるかを見ていきます。
- 50 人の異なる人々のサンプル サイズが測定され、すべての値が次のデータ表に記録されました。スタージェスの規則を適用してデータ セットを間隔に分割し、ヒストグラム上にデータをプロットします。

まず、データを間隔に分割する必要があります。合計で 50 のデータ要素があるため、次の値でスタージェスのルールを使用します。
![Rendered by QuickLaTeX.com \begin{array}{l}c=1+\log_2(N)\\[2ex]c=1+\log_2(50)\\[2ex]c=1+5,64\\[2ex]c=6,64\\[2ex]c\approx 7\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-9929b0c8f1f7cdf5a6160c07e0205c46_l3.png)
したがって、データを分割して 7 つの間隔にグループ化する必要があります。次に、各間隔の幅を知る必要があります。これを行うには、最大値から最小値を引いた値を間隔の合計数で割るだけです。
![]()
つまり、振幅 9 の間隔が 7 つ存在する必要があるため、スタージェス法を使用して計算された間隔は次のようになります。
![]()
![]()
![]()
![]()
![]()
![]()
![]()
間隔を計算したら、各間隔でデータが出現する回数を数え、頻度表を作成する必要があります。
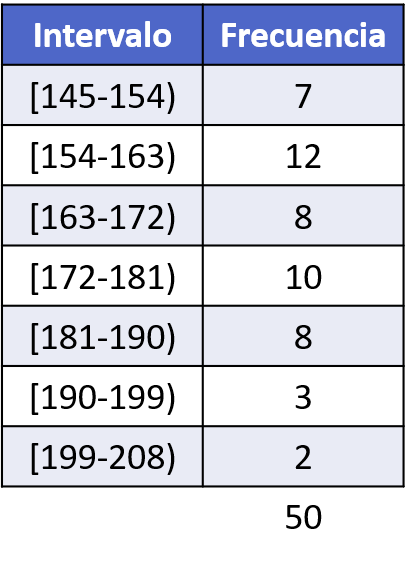
最後に、度数表からヒストグラムを作成してデータをグラフ化できます。
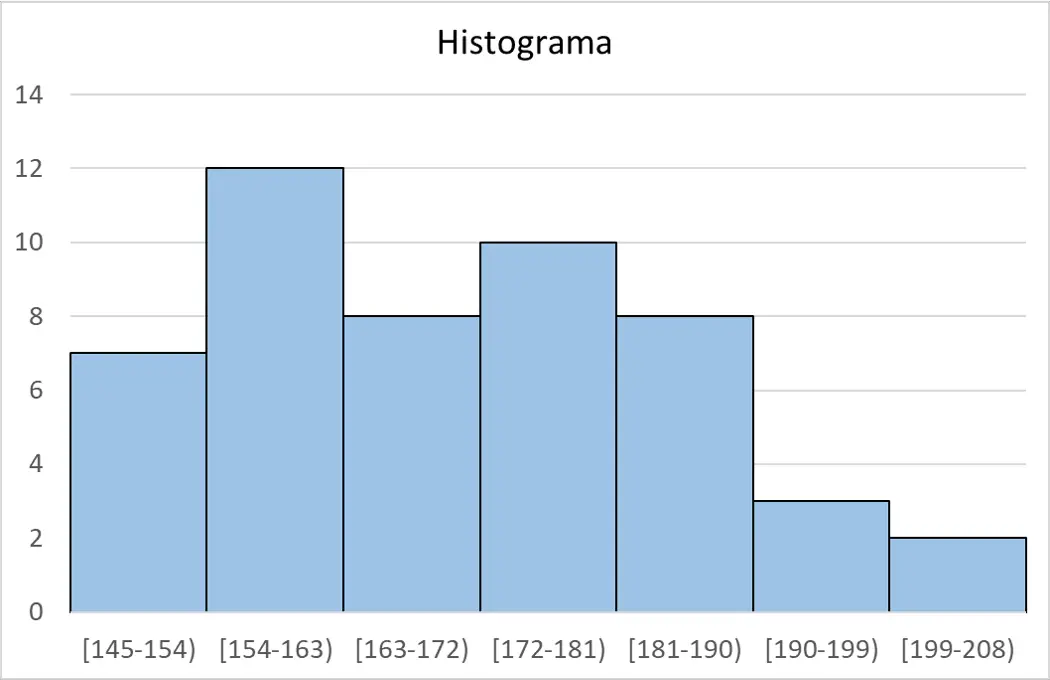
スタージェス則計算機
データサンプルの合計数を入力して「計算」をクリックすると、計算機はスタージェスの法則に従って計算された間隔の数を返します。