円グラフ
この記事では、円グラフとは何か、円グラフの作成方法について説明し、さらに、このタイプの統計グラフを段階的に練習することもできます。
円グラフとは何ですか?
円グラフ、または円グラフ は、統計図の一種であり、データがセクターに分割された円によって表され、各セクターの角度が対応する頻度に比例します。
言い換えれば、値の頻度が高くなるほど、図内の対応するセクターが大きくなります。
したがって、各値の頻度を視覚的に分析するために円グラフが使用されます。統計では、これらのタイプのグラフは主に質的変数を表すために使用されます。
円グラフの作り方
円グラフを作成する手順は次のとおりです。
- 分析したいサンプルから統計データを収集し、度数表を作成します。
- 図の各セクターの角度を計算します。これを行うには、次の式を使用する必要があります。
- 計算された角度から、角度分度器を使用して円グラフ内のセクターを表します。
- 次の式を使用して、グラフ内の各セクターの割合を計算します。
- 各部門の割合を図に示します。
![]()
金
![]()
はセクターiの角度、
![]()
その絶対周波数と
![]()
データの総数。
![]()
金
![]()
はセクターiのパーセンテージ、
![]()
その絶対周波数と
![]()
データの総数。
円グラフの例
円グラフの作成方法を正確に確認できるように、以下に段階的な例を示します。
- 50 人に好きな都市について質問し、そのデータを次の表にまとめました。この統計データを円グラフで表します。

まず、各セクターに対応する角度を計算する必要があるため、各値に次の式を使用します。
![]()
金
![]()
は各セクターの角度、
![]()
その周波数と
![]()
観測の合計数。
たとえば、最初の値に対応するセクターの角度を計算すると、次のようになります。
![]()
次に、角度分度器を使用して計算された角度に対応する扇形を円の中に描きます。
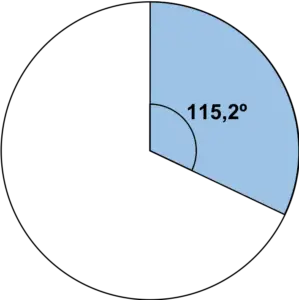
すべての値に対して同じ手順を繰り返します。
![]()
![]()
![]()
![]()
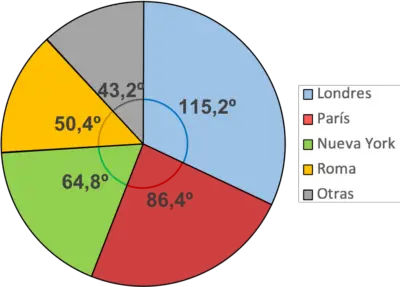
区別しやすくするために、各セクターを異なる色でペイントすることをお勧めします。同様に、各色の意味を示す凡例を追加する必要があります。
すべてのセクターを表現したら、それぞれに対応するパーセンテージを計算する必要があります。これを行うには、次の式を適用します。
![]()
金
![]()
は各セクターの割合です。
![]()
その周波数と
![]()
統計調査のデータの総数。
したがって、各セクターの割合は次のようになります。
![]()
![]()
![]()
![]()
![]()
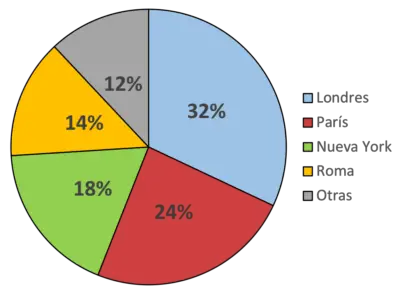
この図では、たとえば、青がロンドン市を表しており、ロンドン市が最も多くの人 (32% の人) が好きな都市であることを示しています。同様に、緑色はニューヨークを表しており、回答者の 18% が好きな都市です。
円グラフの長所と短所
円グラフにはその特性上、次のような長所と短所があります。
アドバンテージ:
- これは非常に視覚的な統計グラフであり、迅速に分析して結論を導き出すことができます。
- 定性的なデータをグラフ化するのに非常に便利です。
- これをコンピューター (Excel など) で実行すると、非常に迅速に実行できます。
短所:
- チャート上にさまざまなセクターが多数ある場合、チャートを読むのが複雑になる可能性があります。この場合、小さなセクターを「その他」という単一のセクターにグループ化することをお勧めします。
- 量的変数や時系列を表すのに適した他のタイプの統計図もあります。