多重比較にダネット検定を使用する方法
ANOVA (分散分析) は、 3 つ以上の独立したグループの平均間に統計的に有意な差があるかどうかを判断するために使用されます。
ANOVA のp 値が特定の選択された有意水準を下回っている場合、帰無仮説を棄却し、グループ平均の少なくとも 1 つが他の平均とは異なると言える十分な証拠があると結論付けることができます。
ただし、これではどのグループが互いに異なるかはわかりません。これは単に、すべてのグループの平均が等しいわけではないことを示しています。どのグループが互いに異なっているかを正確に知るには、 事後テストを実行する必要があります。
研究内のグループの 1 つが対照グループとみなされる場合は、ANOVA 後の事後検定としてダネット検定を使用する必要があります。
ダネット テスト: 定義
次の 2 つの手順を使用してダネット テストを実行できます。
ステップ 1: ダネットのクリティカル値を見つけます。
まず、ダネットの臨界値を見つける必要があります。これは次のように計算されます。
ダネット臨界値: t d √ 2MS w /n
金:
- t d :指定されたアルファ レベル、グループの数、およびグループのサンプル サイズについてダネットのテーブルで見つかった値。
- MS w : ANOVA 出力テーブルの「グループ内」の平均二乗
- n:グループのサンプルサイズ
ステップ 2: グループ平均間の差異をダネットの臨界値と比較します。
次に、各グループの平均と対照グループの平均間の絶対差を計算します。差がダネットの臨界値を超える場合、この差は統計的に有意であると言われます。
次の例は、実際にダネット テストを実行する方法を示しています。
ダネットテスト: 例
教師が 2 つの新しい学習テクニックが生徒のテストの成績を向上させる可能性があるかどうか知りたいと考えているとします。これをテストするために、彼女は 30 人の生徒のクラスを次の 3 つのグループにランダムに分割しました。
- 対照群: 10 人の学生
- 新しい技術学習 1: 学生 10 名
- 新技術学習2:10名
割り当てられた学習方法を 1 週間使用した後、各生徒は同じ試験を受けます。結果は次のとおりです。
- 対照群の平均試験スコア: 81.6
- 新勉強法グループ1の試験平均点: 85.8点
- 新勉強法2 集団試験の平均点: 87.7
- ANOVA 出力テーブルの「グループ内」の平均二乗: 23.3
この情報を使用して、ダネット テストを実行して、2 つの新しい学習手法のうちの 1 つが対照グループと比べて試験の平均点に大幅に差があるかどうかを判断できます。
ステップ 1: ダネットのクリティカル値を見つけます。
α = 0.05、グループのサンプル サイズ n = 10、およびグループの合計 = 3 を使用すると、ダネットの表では臨界値の計算に2.57の値を使用することがわかります。
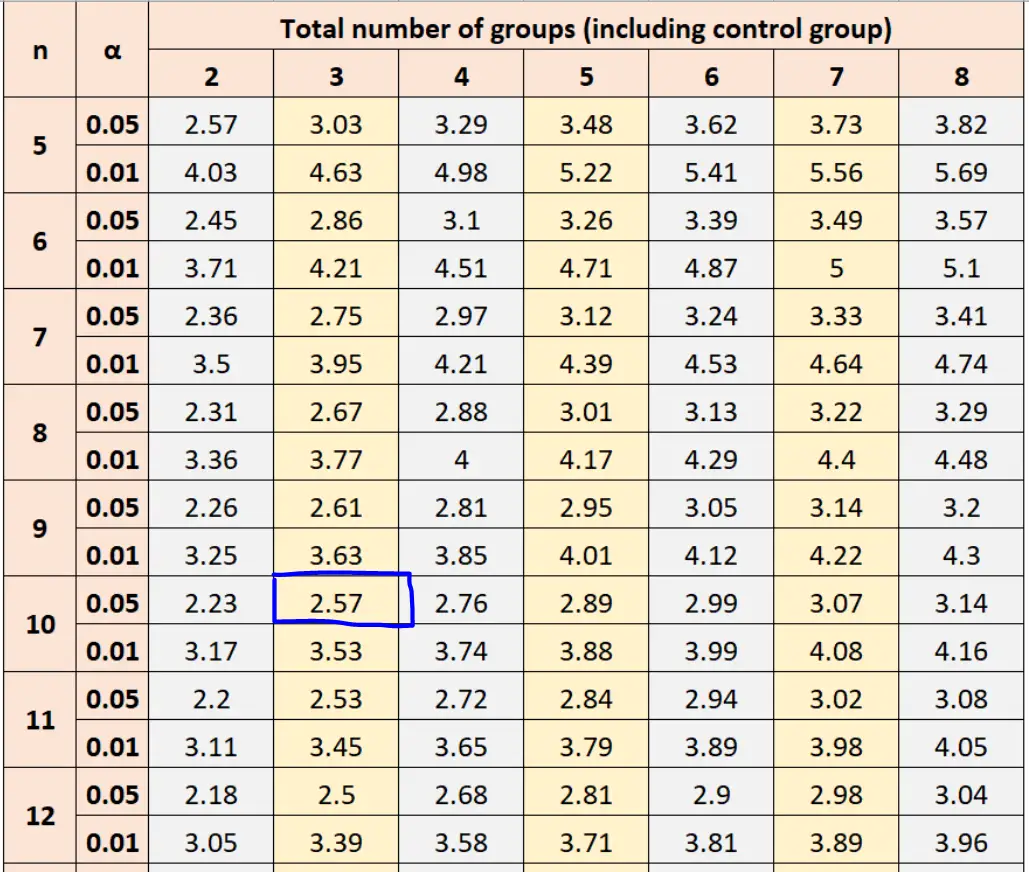
次に、この数値を式に代入して、重要なダネット値を見つけることができます。
ダネットの臨界値: t d √ 2MS w /n = 2.57√ 2(23.3)/10 = 5.548
ステップ 2: グループ平均間の差異をダネットの臨界値と比較します。
各研究手法の平均値と対照群の平均値との絶対的な差は次のとおりです。
- 腹筋新しいテクニック 1 とコントロールの差: |85.8 – 81.6| = 4.2
- 腹筋新しいテクニック 2 とコントロールの差分: |87.7 – 81.6| = 6.1
手法 2 と対照グループ間の絶対差のみがダネット臨界値5,548より大きくなります。
したがって、新しい学習手法 #2 は対照群と比べて著しく異なる試験結果をもたらしたと言えますが、これは新しい学習手法 #1 には当てはまりません。