パレート図
この記事では、パレート図とは何かについて説明します。したがって、パレート図がどのように構築されるか、このタイプの統計グラフの例、およびパレート図を解釈する方法がわかります。
パレート図とは何ですか?
パレート図は、一連のデータを降順の棒で表す統計グラフの一種です。さらに、パレート図では、累積パーセンテージが度数多角形を使用してグラフ化されます。
パレート図は、問題を分析し、その主な原因を特定するために使用されます。実際、パレート図はパレートの法則の基礎です。この統計規則がどのような構成になっているかを以下で説明します。
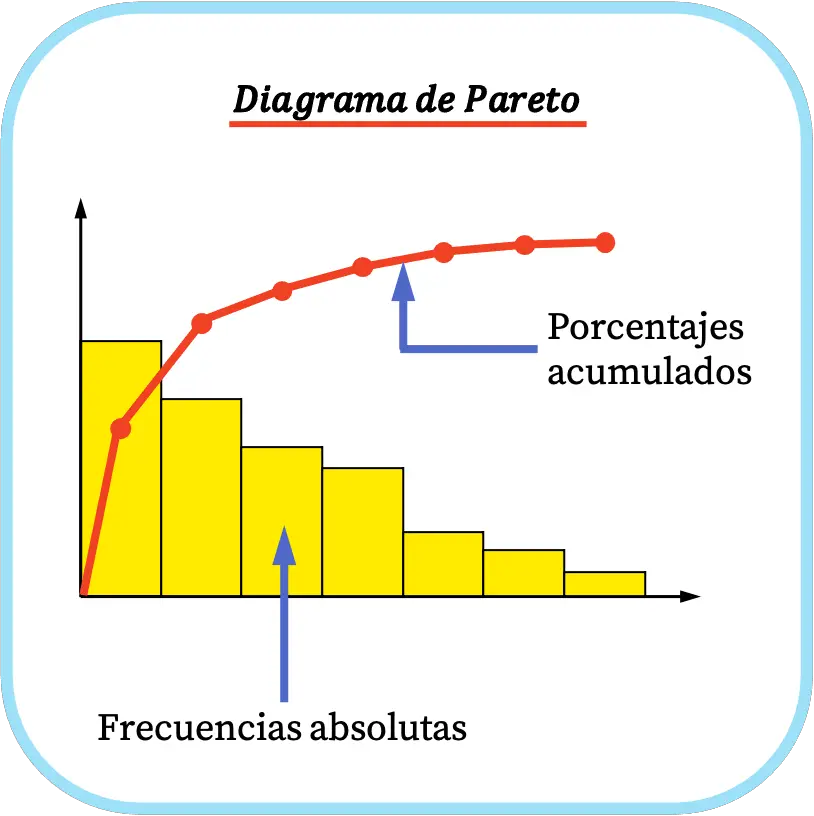
パレート図は閉曲線またはABC 分布としても知られ、イタリアの経済学者ヴィルフレド パレートによって発明されました。
パレート図の作り方
パレート図を作成する手順は次のとおりです。
- 分析する問題に関する統計データを収集します。
- 値を絶対頻度に基づいて降順、つまり絶対頻度が最も高いものから最も低いものに並べ替えます。
- 各カテゴリの割合を計算します。これを行うには、カテゴリの絶対頻度をデータの総数で割り、100 を掛けます。
- カテゴリのパーセンテージと以前のすべてのパーセンテージの合計である累積パーセンテージを決定します。
- 絶対周波数をバーを使用してグラフで表し、周波数多角形を使用して累積パーセンテージを表します。
以下に、パレート図を作成する実際の例を示します。
パレート図の例
パレート図の定義を理解したところで、このタイプの図を作成する方法を段階的に説明する例を見ていきます。
- コンピューターの販売に関する統計調査のために、50 人のサンプルにコンピューターを購入する主な理由を尋ね、その結果を次のデータ表に記録しました。回答者の回答を使用してパレート図を作成します。
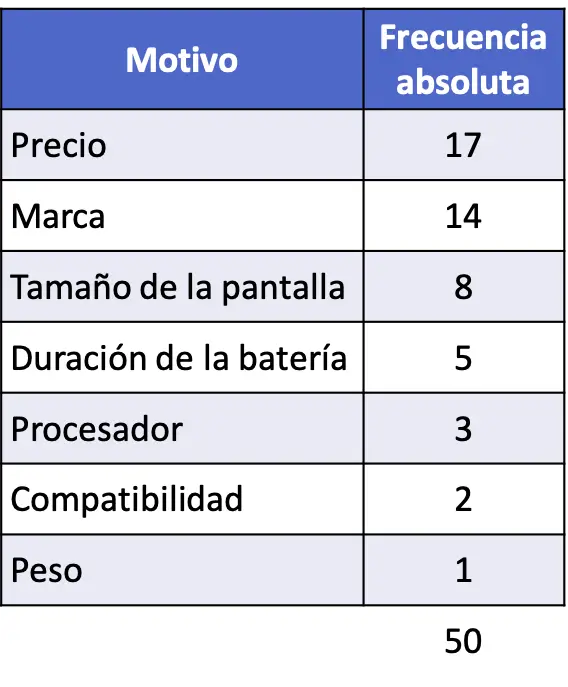
この場合、データはすでに最高から最低の順に並べられているため、各値のパーセンテージが計算されます。これを行うには、絶対頻度を観測値の総数で割ってから 100 を掛けます。
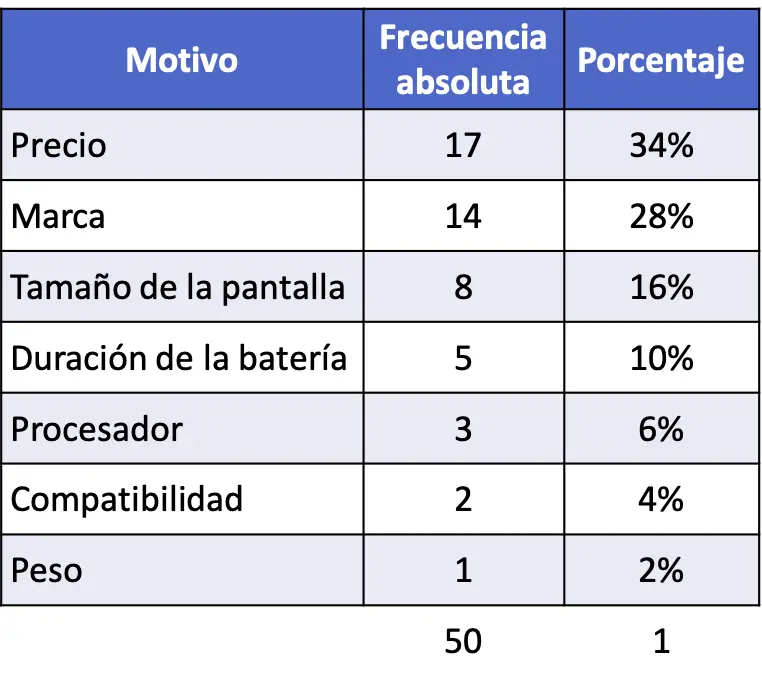
ここで、各値のパーセンテージと以前のすべてのパーセンテージを加算して、累積パーセンテージを計算します。
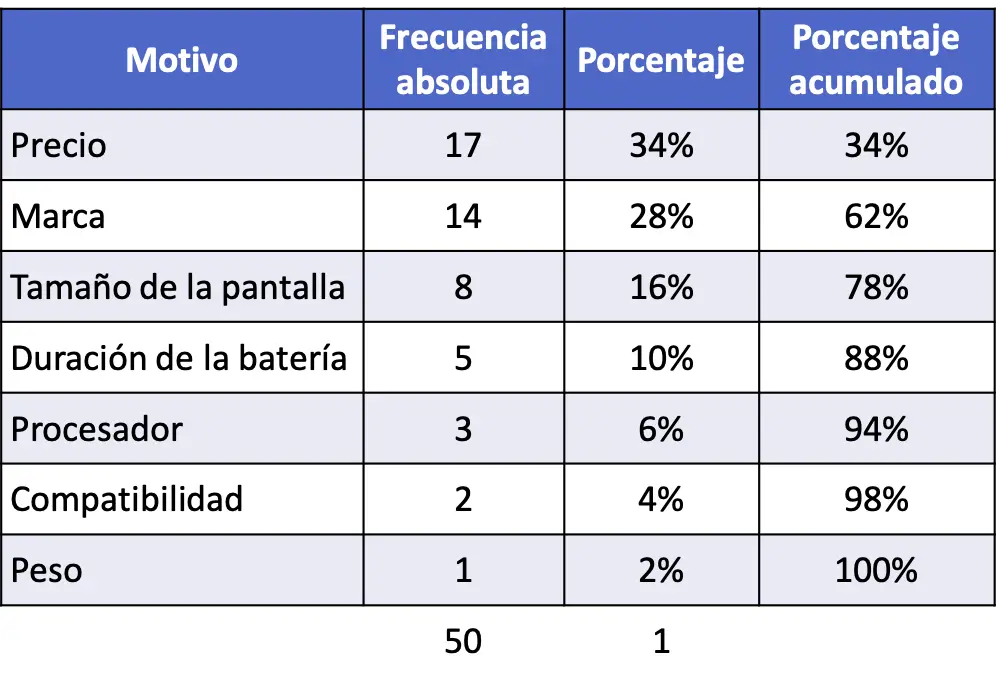
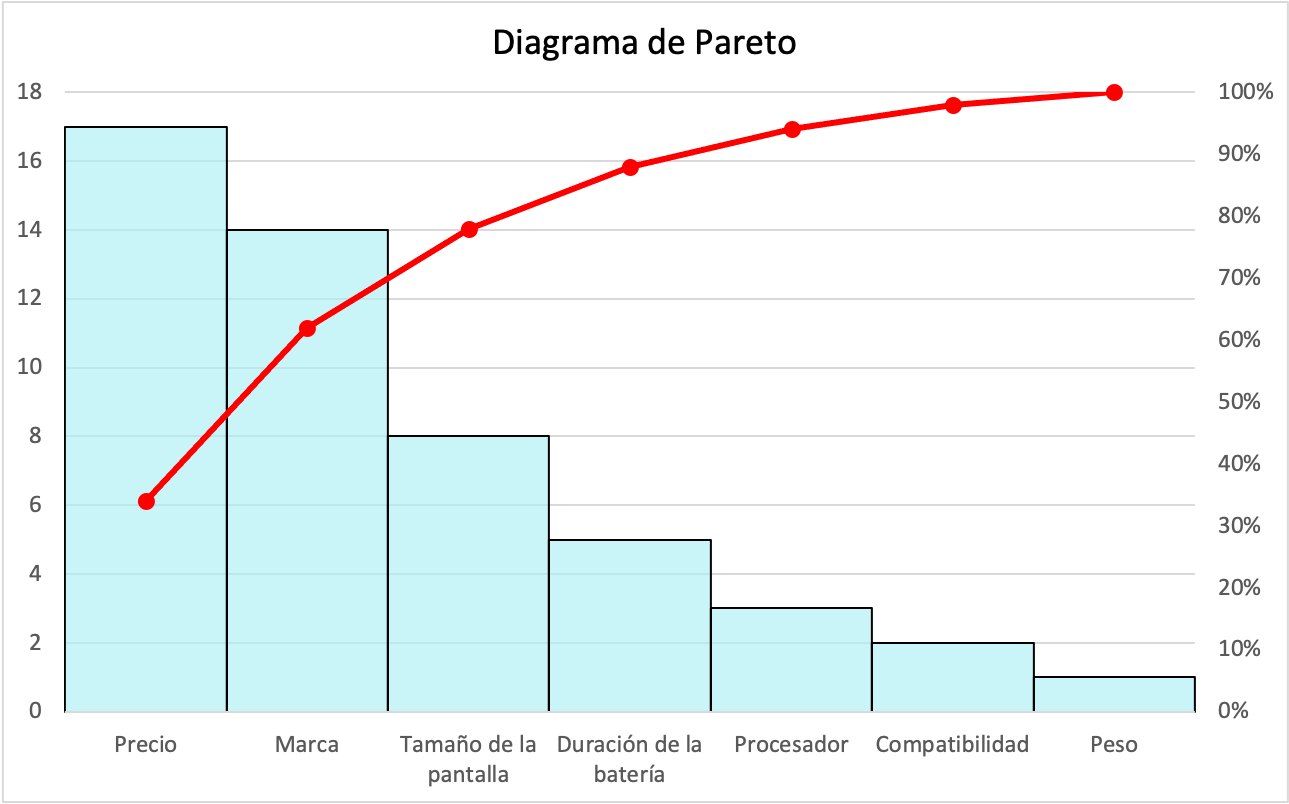
必要な計算をすべて完了したら、パレート図でのデータのグラフ化に進みます。絶対周波数は長方形のバーで表され、累積パーセンテージは周波数多角形で表されます。
パレート図は何に使用されますか?
統計では、パレート図は問題を分析し、その原因を特定するために使用されます。パレート図は主に、問題の理由と、全体に対する考えられるそれぞれの原因の重要性を見つけるために使用されます。
パレート図は、絶対頻度と累積パーセンテージを同時に視覚化できるため、分析を行って問題の最も重要な原因を特定するのに役立ちます。
さらに、パレートの法則(またはパレートの法則) はパレート図から派生したもので、結果の 80% は原因の 20% から生じる、つまり、結果の 80% は原因の 20% から生じるというものです。原因。原因。活動。上の例を見ると、最初の 2 つの回答は、残りの可能な回答よりもはるかに高い割合を表しています。
さらに、パレート図は品質管理で広く使用されている図です。実はこれ、言わずと知れた「石川七道具」の一つに数えられているんです。
パレート図と棒グラフの違い
パレート図と棒グラフの違いは、パレート図は降順に配置され、累積パーセンテージを含む度数多角形が含まれていることです。一方、棒グラフでは絶対周波数のみが任意の順序で表示されます。
これは、パレート図が棒グラフよりも優れているということではありません。このタイプのグラフは常にグラフィカルに表現する必要があり、各グラフには長所と短所があります。
すべての棒グラフの機能を表示するには、ここをクリックしてください。