T 検定から p 値を手動で計算する方法
統計で最もよく使用される検定の 1 つはt 検定で、母集団の平均が特定の値に等しいかどうかを判断するためによく使用されます。
たとえば、特定の植物種の平均高さが 15 インチに等しいかどうかを知りたいとします。これをテストするには、20 本の植物の ランダム サンプルを収集し、サンプル平均とサンプル標準偏差を求め、t 検定を実行して平均高さが実際に 15 インチであるかどうかを判断します。
検定の帰無仮説と対立仮説は次のとおりです。
H 0 : μ = 15
H a : μ ≠ 15
検定統計量の式は次のとおりです。
t = ( X -μ) / (s/ √n )
ここで、 xはサンプル平均、 μは仮説平均 (この例では 15)、 sはサンプル標準偏差、 nはサンプルサイズです。
tの値がわかったら、統計ソフトウェアまたはオンライン計算機を使用して、対応する p 値を見つけることができます。 p 値が特定のアルファ レベル (一般的な選択肢は 0.01、0.05、および 0.10) を下回っている場合、帰無仮説は棄却され、平均植物の高さは 15 インチではないと結論付けることができます。
ただし、 t 分布表を使用して検定 p 値を手動で推定することもできます。この記事ではその方法を説明します。
例: t 検定からの p 値の手動計算
問題: ボブは、特定の植物種の平均高さが 15 インチに等しいかどうかを知りたいと考えています。これをテストするために、20 本の植物から無作為にサンプルを収集したところ、サンプルの平均は 14 インチ、サンプルの標準偏差は 3 インチであることがわかりました。アルファ レベル 0.05 を使用して t 検定を実行し、母集団の真の平均身長が実際に 15 インチであるかどうかを判断します。
解決:
ステップ 1: 帰無仮説と対立仮説を述べます。
H 0 : μ = 15
H a : μ ≠ 15
ステップ 2: 検定統計量を見つけます。
t = ( x -μ) / (s/ √n ) = (14-15) / (3/ √20 ) = -1.49
ステップ 3: 検定統計量の p 値を見つけます。
p 値を手動で見つけるには、n-1 自由度の t 分布テーブルを使用する必要があります。この例では、サンプル サイズは n = 20 なので、n-1 = 19 となります。
以下の t 分布表では、左側の「19」に対応する行を見て、検定統計量1.49の絶対値を見つけようとする必要があります。
1.49 は表には表示されませんが、 1.328と1.729の 2 つの値の間にあることに注意してください。
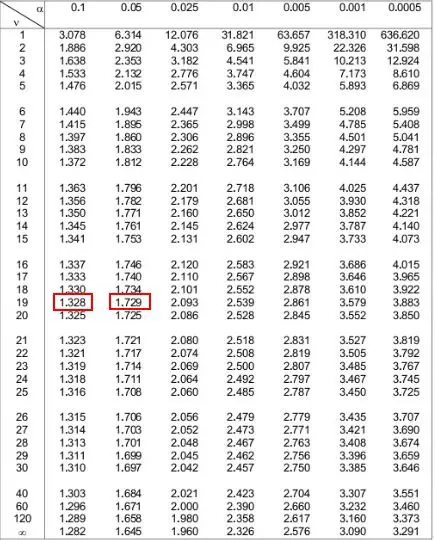
次に、これら 2 つの数値に対応するテーブルの上部にある 2 つのアルファ レベルを確認します。それらが0.1と0.05であることがわかります。
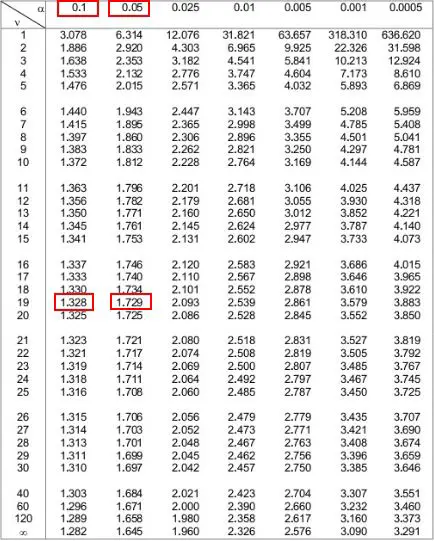
これは、片側検定の p 値が 0.1 ~ 0.05 であることを意味します。それを.075と呼びましょう。 t 検定は両側であるため、この値に 2 を掛ける必要があります。したがって、推定される p 値は 0.075 * 2 = 0.15となります。
ステップ 4: 結論を導き出します。
この p 値は選択したアルファ レベル 0.05 より低くないため、帰無仮説を棄却できません。したがって、この植物種の真の平均高さが 15 インチ以外であると言える十分な証拠はありません。
計算機で結果を確認する
t検定統計量と自由度をオンラインの p 値計算ツールに接続して、推定された p 値が真の p 値にどの程度近かったかを確認できます。

真の p 値は0.15264で、推定の p 値0.15にかなり近い値です。
結論
この記事では、t 分布表を使用して t 検定の p 値を手動で推定できることを説明しました。ただし、ほとんどのシナリオでは p 値を手動で計算する必要はなく、R や Excel などの統計ソフトウェアまたはオンライン計算機を使用して検定の正確な p 値を見つけることができます。
ほとんどの場合、特に厳密な統計研究や実験では、電卓を使用して t 検定から正確な p 値をできるだけ正確に求める必要がありますが、いつでも手動で推定できることを知っておくと良いでしょう。どうしても必要な場合は、t 検定の p 値を使用します。