ピアソン相関関係の 5 つの仮説
ピアソン相関係数(「積率相関係数」とも呼ばれる) は、2 つの変数間の線形関連性を測定します。
常に -1 から 1 までの値を取ります。
- -1 は、2 つの変数間の完全な負の線形相関を示します。
- 0 は 2 つの変数間に線形相関がないことを示します
- 1 は、2 つの変数間の完全な正の線形相関を示します。
ただし、2 つの変数間のピアソン相関係数を計算する前に、次の 5 つの仮定が満たされていることを確認する必要があります。
1. 測定レベル:両方の変数は間隔または比率レベルで測定される必要があります。
2. 線形関係: 2 つの変数間には線形関係がなければなりません。
3. 正規性:両方の変数がほぼ正規分布になる必要があります。
4. 関連ペア:データセット内の各観測値には値のペアが必要です。
5. 外れ値がない:データセットに極端な外れ値があってはなりません。
この記事では、各仮定の説明と、その仮定が満たされているかどうかを判断する方法を説明します。
仮説 1: 測定レベル
2 つの変数間のピアソン相関係数を計算するには、両方の変数を間隔または比率レベルで測定する必要があります。
次の図は、変数を測定できる 4 つのレベルを簡単に説明しています。
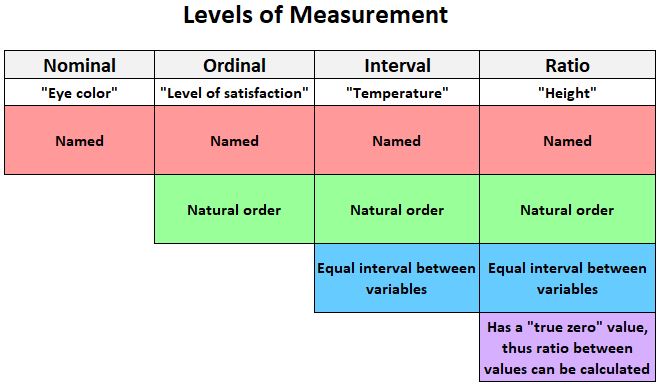
以下に、間隔スケールで測定できる変数の例をいくつか示します。
- 温度:華氏または摂氏で測定
- 信用スコア: 300 ~ 850 で測定
- SAT スコア: 400 ~ 1,600 で測定
以下に、比率スケールで測定できる変数の例をいくつか示します。
- 高さ:センチメートル、インチ、フィートなどで測定されます。
- 重量:キログラム、ポンドなどで測定されます。
- 長さ:センチメートル、インチ、フィートなどで測定されます。
変数が順序レベルで測定される場合は、変数間の スピアマン相関係数を計算する必要があります。
関連:測定レベル: 名目、順序、間隔、比率
仮説 2: 線形関係
2 つの変数間のピアソン相関係数を計算するには、2 つの変数間に線形関係が存在する必要があります。
この仮説をテストする最も簡単な方法は、2 つの変数の散布図を作成することです。プロット上の点がほぼ直線に従っている場合、線形関係が存在します。
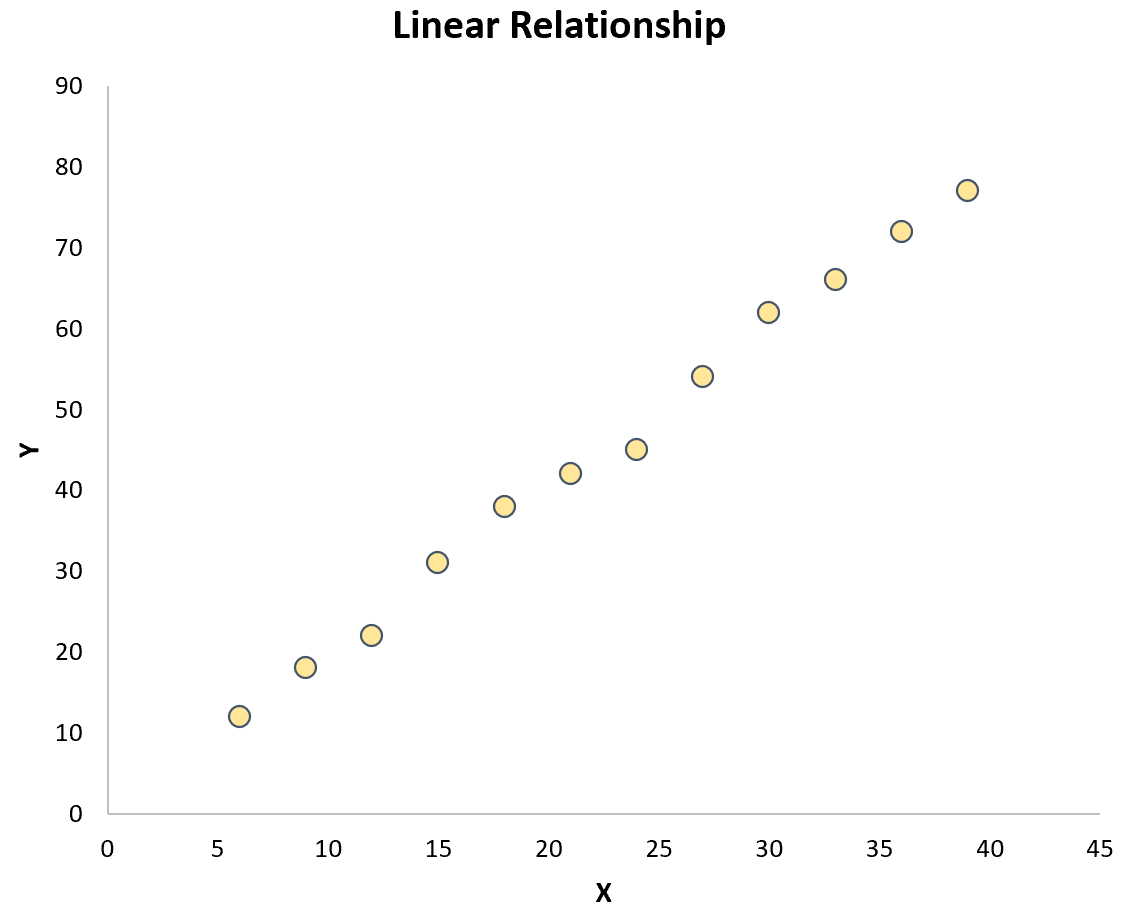
ただし、点がプロット全体にランダムに散在している場合、または他のタイプの関係 (二次関数など) がある場合、変数間に線形関係は存在しません。
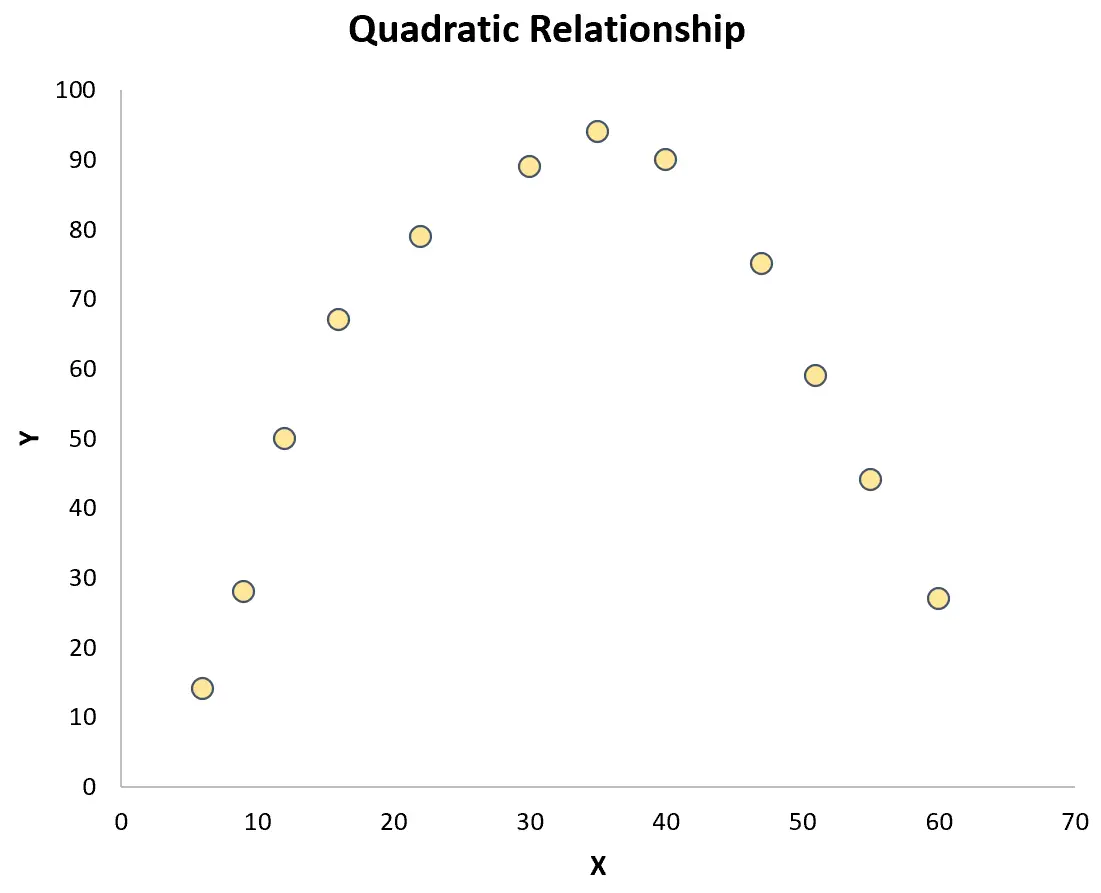
この場合、ピアソン相関係数は変数間の関係を適切に捉えることができません。
仮説 3: 正常性
ピアソン相関係数は、2 つの変数がほぼ正規分布していることも前提としています。
この仮定は、変数ごとにヒストグラムまたは QQ プロットを作成することで視覚的に検証できます。
1. ヒストグラム
データセットのヒストグラムがほぼ釣鐘型の場合、データは正規分布している可能性があります。

2.QQランド
「分位数-分位数」の略である QQ プロットは、X 軸に沿って理論的な分位数 (つまり、正規分布に従った場合のデータの位置) と、Y 軸に沿ってサンプルの分位数を表示するプロットの一種です。 (つまり、データが実際に存在する場所)。
データ値が 45 度の角度を形成するほぼ直線に従っている場合、データは正規分布しているとみなされます。

正式な統計検定を実行して、変数が正規分布しているかどうかを判断することもできます。
検定のp 値が特定の有意水準 (α = 0.05 など) を下回っている場合、データが正規分布していないことを示す十分な証拠があります。
正規性をテストするために一般的に使用される 3 つの統計テストがあります。
1. ハルケ・ベラ・テスト
2. シャピロ・ウィルク・テスト
3. コルモゴロフ・スミルノフ検定
仮説 4: 関連するペア
ピアソン相関係数は、データセット内の各観測値が値のペアを持つ必要があることも前提としています。
この仮説は簡単に検証できます。たとえば、体重と身長の相関関係を計算する場合は、データセット内の各観測値に体重の測定値と身長の測定値が含まれていることを確認するだけです。
仮説 5: 外れ値はありません
ピアソン相関係数では、外れ値は相関係数の計算に大きな影響を与えるため、データセットに極端な外れ値が存在しないことも前提としています。
これを説明するために、次のデータセットを考えてみましょう。
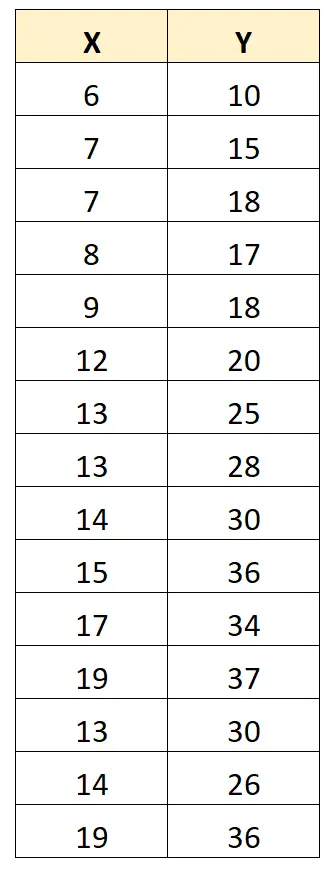
X と Y の間のピアソン相関係数は0.949です。
ただし、データセットに外れ値があるとします。
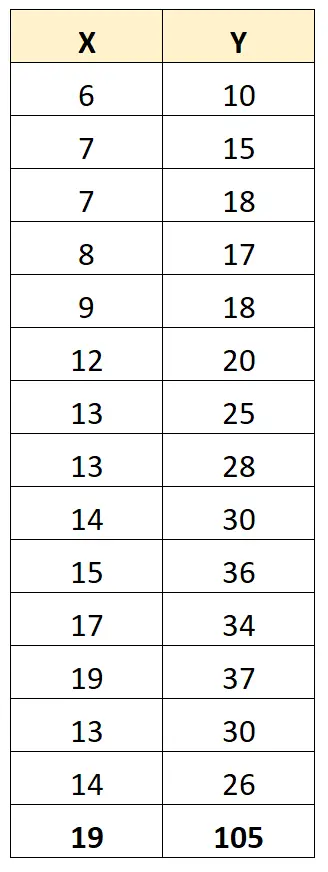
X と Y の間のピアソン相関係数は0.711になりました。
外れ値があると、2 つの変数間のピアソン相関係数が大きく変化します。この場合、データセットから外れ値を削除することが合理的である可能性があります。
追加リソース
次のチュートリアルでは、ピアソン相関に関する追加情報を提供します。