ヒストグラム
この記事では、ヒストグラムとは何か、何に使用されるか、ヒストグラムを解釈する方法について説明します。したがって、ヒストグラムの作成方法と、あらゆる種類のヒストグラムの例がわかります。
ヒストグラムとは何ですか?
ヒストグラムは統計グラフの一種で、一連の統計データが長方形のバーで表され、ヒストグラム内の各バーが対応する頻度に比例します。
ヒストグラムは、統計サンプルの重みなどの連続変数をグラフ化するために使用されます。さらに、ヒストグラムを使用すると、分布の形状をすばやく視覚化できます。
頻度ヒストグラムの各バーの幅は間隔の幅に比例し、高さは間隔の頻度に比例します。
ヒストグラムの作り方
ヒストグラムを作成する手順は次のとおりです。
- データ系列に基づいてヒストグラムの横軸をグループに分割します。
- ヒストグラムの縦軸に間隔頻度値をプロットします。
- 間隔ごとに、間隔の周波数に等しい高さの長方形のバーを描画します。連続する 2 つの間隔のバーが接触している必要があることに注意してください。
ヒストグラムの例
ヒストグラムの定義と関連する理論を理解したら、以下にこのタイプの統計グラフがどのように作成されるかの例を説明します。
- 次の頻度表に示すように、衣料品店は 1 日に異なる価格で 50 個の商品を販売します。記録された販売データからヒストグラムを作成します。
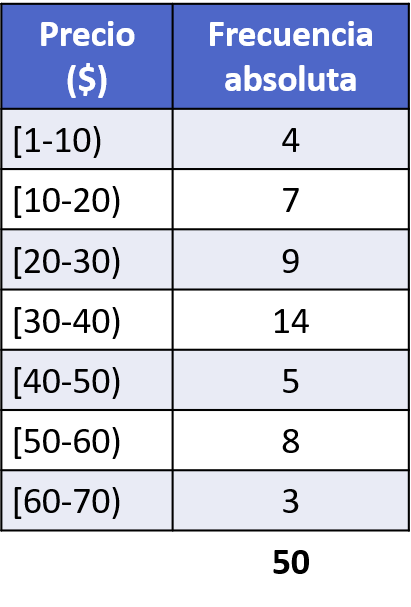
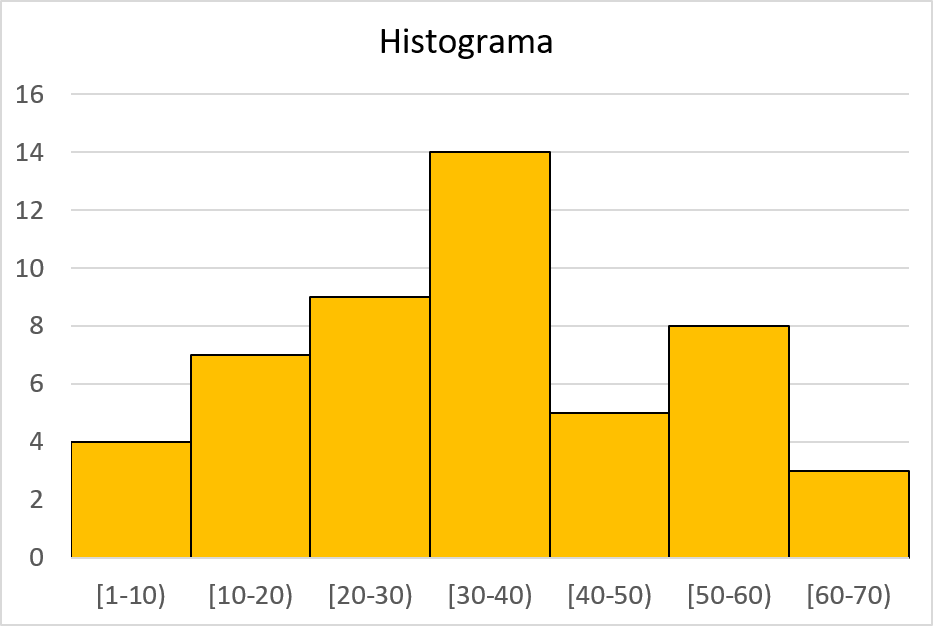
ヒストグラムを表すには、上で説明した手順に従う必要があります。つまり、最初に横軸をデータの間隔に相当する部分に分割し、次に縦軸のスケールを調整し、最後に各間隔を絶対頻度で同じ高さの列で表します。
相対頻度ヒストグラム
相対度数ヒストグラムは、データセットの相対度数を表すヒストグラムの一種です。つまり、絶対周波数をグラフ化する代わりに、相対周波数をグラフ化します。
異なる度数が表されていますが、相対度数ヒストグラムの形状は絶対度数ヒストグラムの形状と同じであり、単に縦軸の値を変更するだけです。
例として、前の演習の統計的研究から相対頻度ヒストグラムを構築します。これを行うには、まず各間隔の相対頻度を計算する必要があります。これは、絶対頻度をデータの総数 (50) で割ったものに相当します。
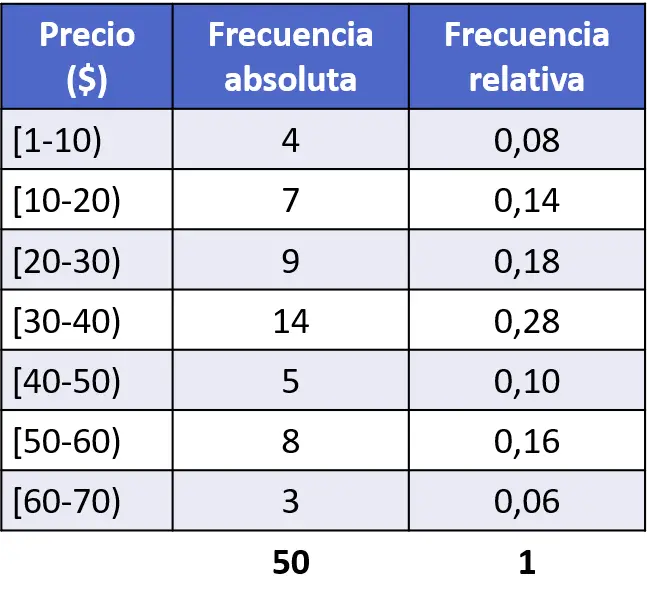
相対頻度を計算したら、それらをヒストグラムにグラフ化するだけです。これを行うには、販売されたユニットの価格に対応する横軸を描き、次に相対頻度を表す縦軸を描き、最後に各間隔ごとに相対頻度に等しい高さの長方形の棒を描きます。 。頻度。
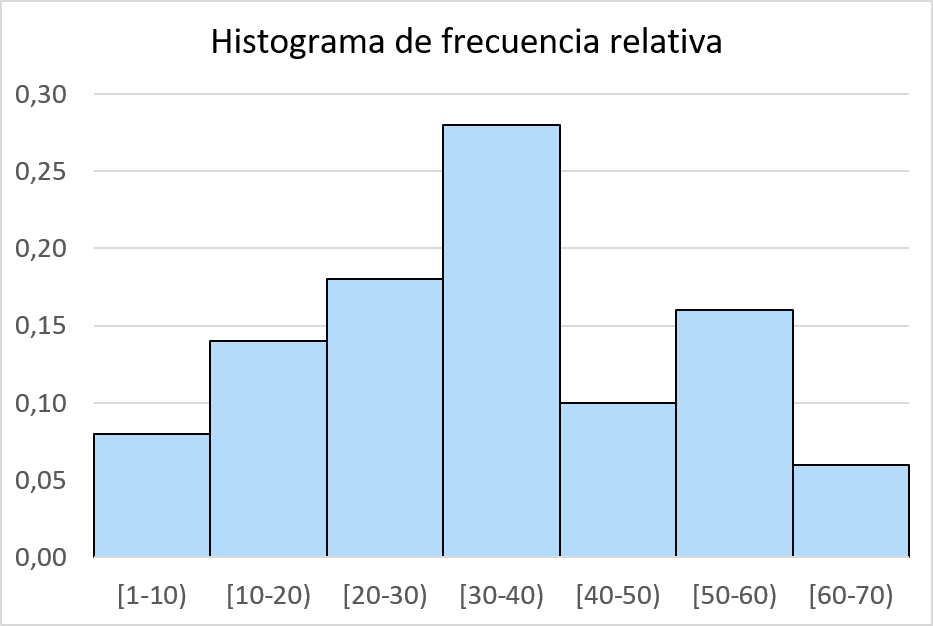
累積頻度ヒストグラム
絶対頻度ヒストグラムと相対頻度ヒストグラムの作成方法を説明しましたが、統計では累積頻度ヒストグラムも使用されます。
累積度数ヒストグラムは、累積度数をプロットしたヒストグラムの一種です。つまり、累積頻度ヒストグラムでは、絶対頻度ではなく累積頻度が表されます。
論理的には、絶対頻度と相対頻度を使用して累積頻度ヒストグラムを作成できます。例として、この記事全体で行う演習と同じデータを使用して、これら 2 種類のヒストグラムを以下に示します。
累積絶対頻度のヒストグラム
明らかに、累積絶対頻度のヒストグラムをプロットするには、まず各間隔の累積絶対頻度を決定する必要があります。これを行うには、各間隔における以前のすべての絶対周波数と、問題の間隔の絶対周波数を加算します。
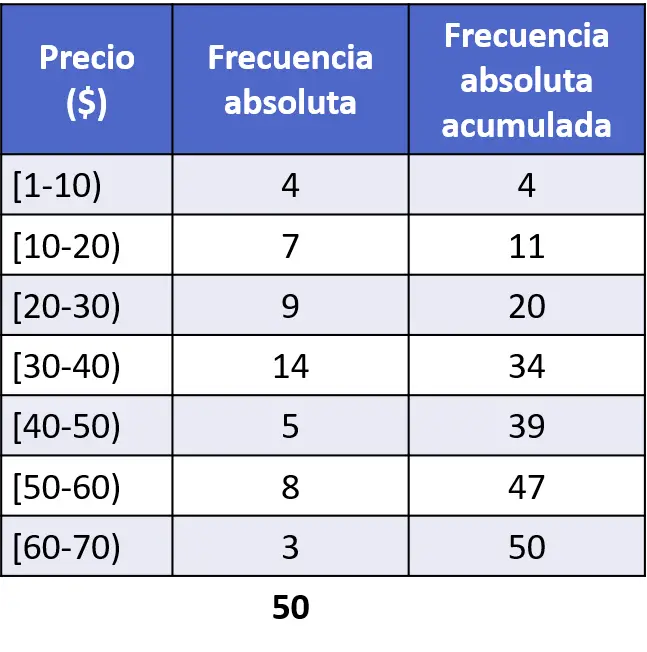
したがって、計算が完了したので、同じ手順に従ってヒストグラムをプロットしますが、累積絶対頻度を使用します。
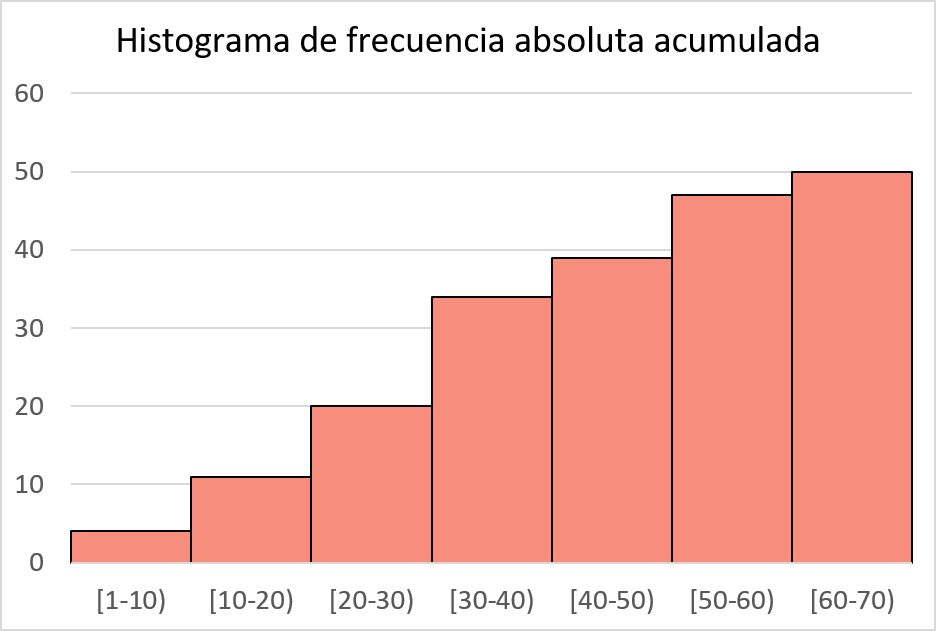
累積相対度数のヒストグラム
累積相対度数のヒストグラムは、累積絶対度数と同じ方法で作成されます。まず、データ系列の累積相対度数を計算します。
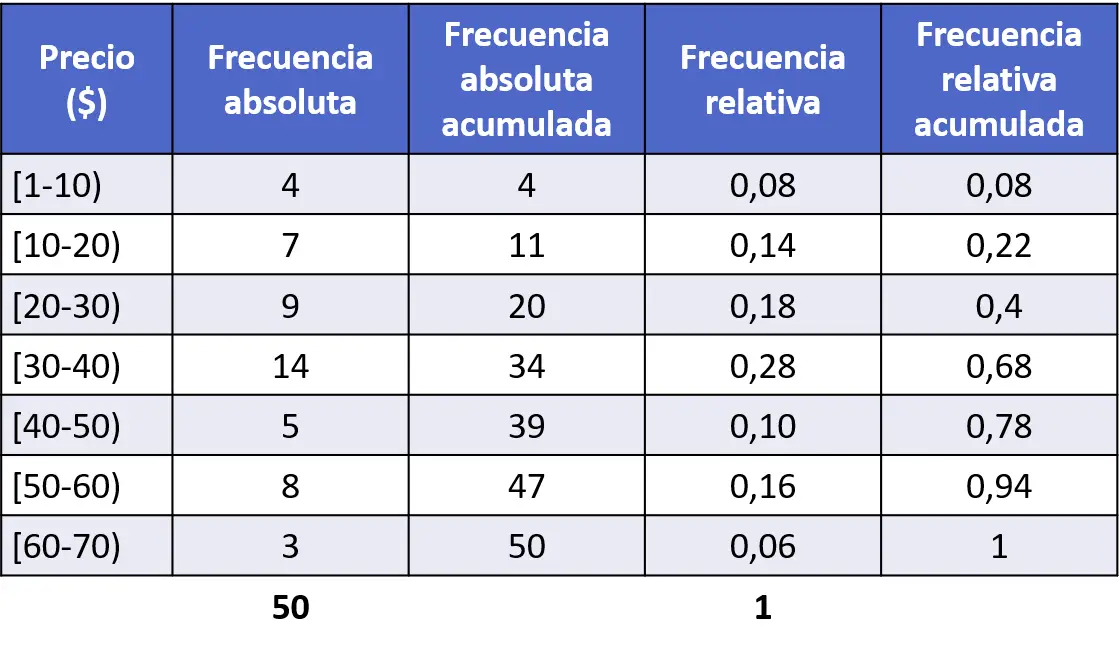
次に、累積相対頻度をヒストグラムで表します。
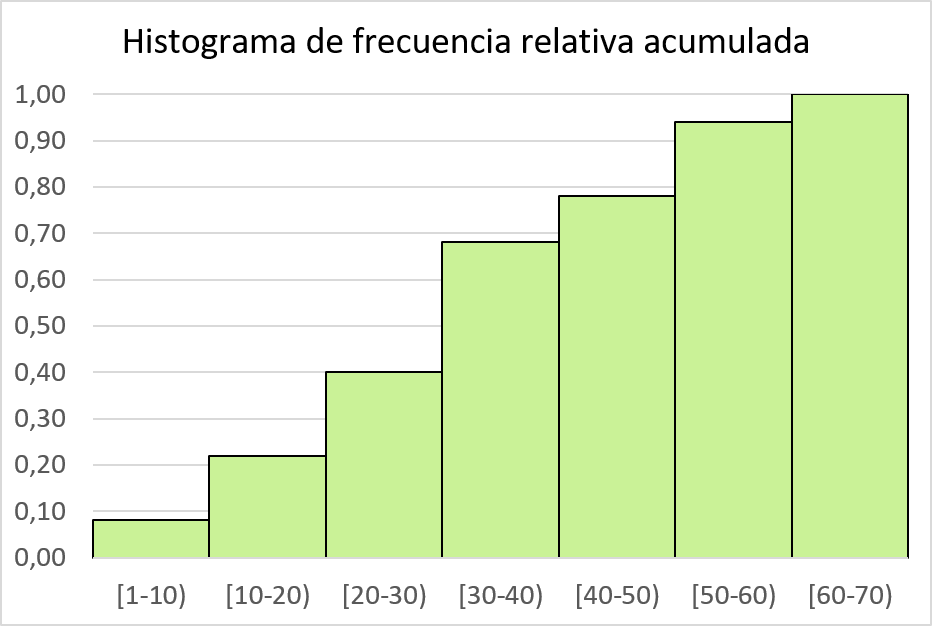
ヒストグラムと頻度多角形を組み合わせる
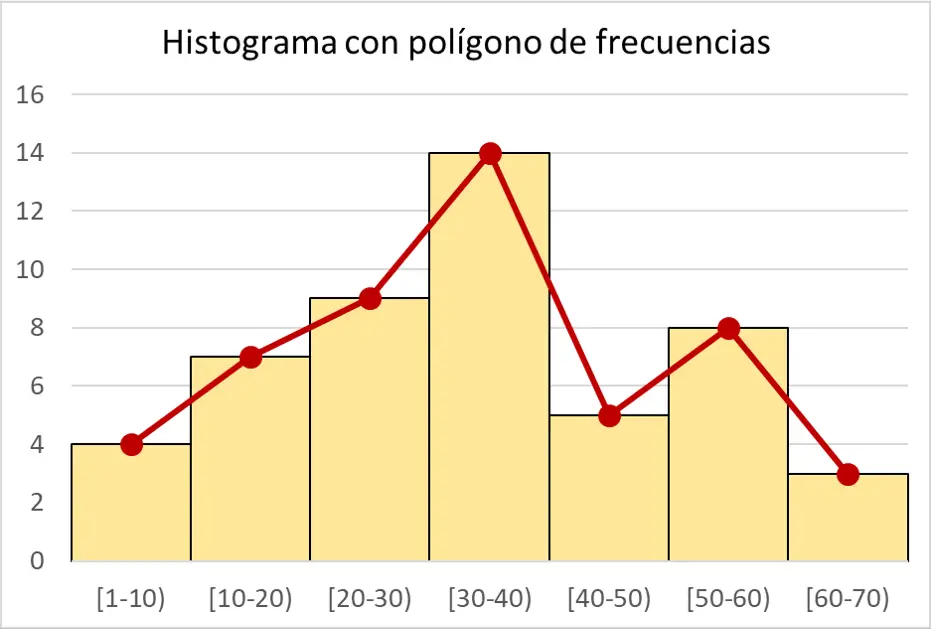
統計では、ヒストグラムが直線で結ばれた一連の点である頻度多角形と組み合わされることがあります。このようにして、周波数多角形の線によってデータ系列の進行をより適切に視覚化できるため、データの変化がより明確に示されます。
これら 2 種類の統計プロットを組み合わせるには、各長方形のヒストグラム バーの上端の中央に点をプロットし、連続する点を直線で結びます。
たとえば、この投稿の冒頭で作成した絶対周波数のヒストグラムと周波数ポリゴンを組み合わせたものは次のとおりです。