R で fitdistr() を使用して分布を近似する方法

R のMASSパッケージのfitdistr()関数を使用すると、尤度関数を最大化することで分布のパラメーターを推定できます。

この関数は次の基本構文を使用します。

fitdistr(x、densefun、…)

金：

• x : 分布の値を表す数値ベクトル
• Densityfun : パラメータを推定するための分布

densfun引数は、次の潜在的な分布名を受け入れることに注意してください: beta 、 cauchy 、 chi-square 、 exponential 、 gamma 、 geometric 、 lognormal 、 logistic 、 negative binomial 、 normal 、 Poisson 、 t 、およびWeibull 。

次の例は、実際にfitdistr()関数を使用する方法を示しています。

例: fitdistr() 関数を使用して R で分布を近似する方法

R でrnorm()関数を使用して、正規分布に従う 200 個の値のベクトルを生成するとします。

 #make this example reproducible
set. seeds (1)

#generate sample of 200 observations that follows normal dist with mean=10 and sd=3
data <- rnorm(200, mean=10, sd=3)

#view first 6 observations in sample
head(data)

[1] 8.120639 10.550930 7.493114 14.785842 10.988523 7.538595

hist()関数を使用してヒストグラムを作成し、データ値の分布を視覚化できます。

 hist(data, col=' steelblue ')

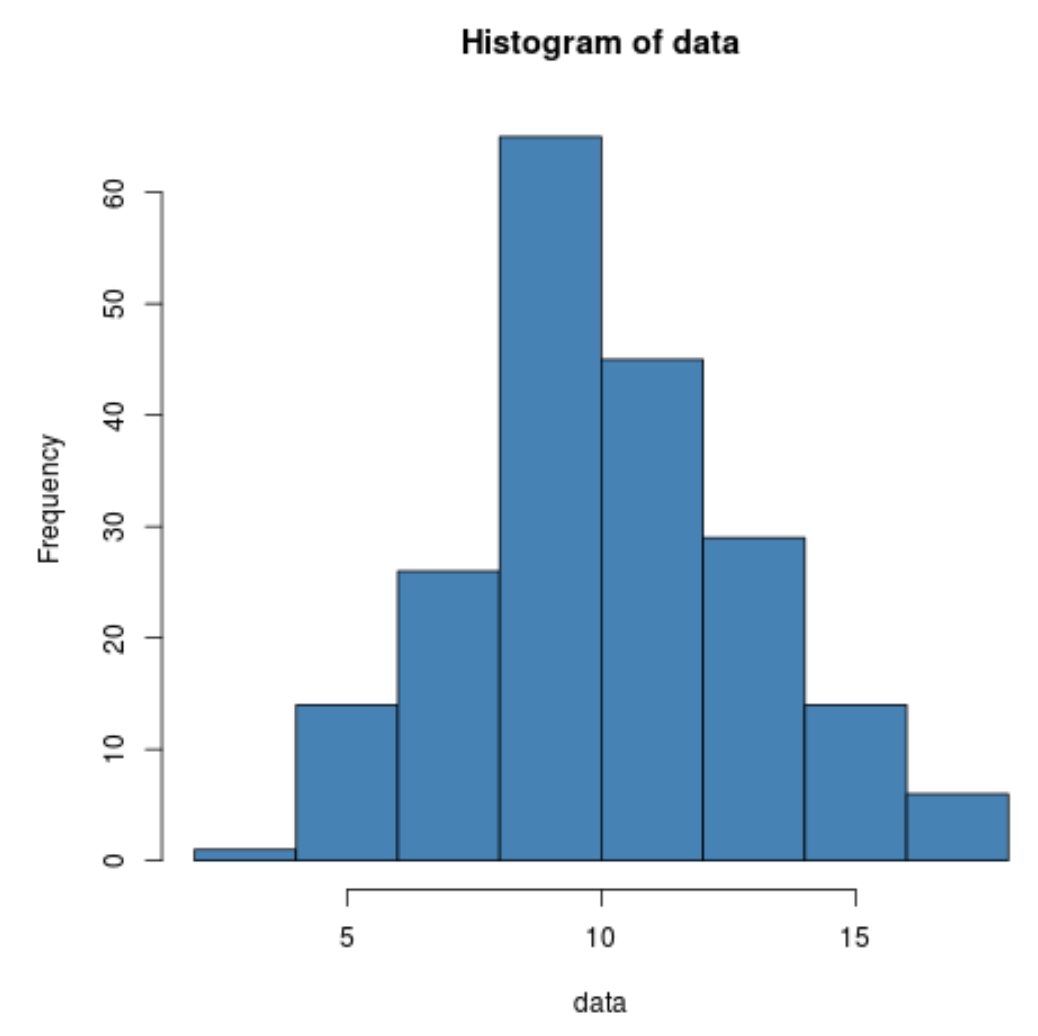
データが実際に正規分布していることがわかります。

次に、 fitdistr()関数を使用して、この分布のパラメーターを推定できます。

 library (MASS)

#estimate parameters of distribution
fitdistr(data, “ normal ”)

      mean sd    
  10.1066189 2.7803148 
 (0.1965979) (0.1390157)

fitdistr()関数は、値のベクトルが平均10.1066189と標準偏差2.7803148の正規分布に従うと推定します。

rnorm()関数を使用して平均値 10、標準偏差 3 のデータを生成したため、これらの値は驚くべきことではありません。

追加リソース

次のチュートリアルでは、R で他の一般的なタスクを実行する方法について説明します。

R で正規分布をプロットする方法
R で正規分布を生成する方法
R で正規性について Shapiro-Wilk テストを実行する方法