フリードマン テスト: 定義、公式、例
フリードマン検定は、 反復測定 ANOVA に代わるノンパラメトリックな検定です。
各グループに同じ被験者が含まれる 3 つ以上のグループの平均値の間に統計的に有意な差があるかどうかを判断するために使用されます。
フリードマンテストをいつ使用するか
フリードマン テストは通常、次の 2 つの状況で使用されます。
1. 3 つ以上の時点にわたる被験者の平均スコアを測定します。
たとえば、トレーニング プログラムを開始する 1 か月前、プログラムを開始してから 1 か月後、プログラムを使用してから 2 か月後に被験者の残りの心拍数を測定するとします。フリードマン テストを実行すると、これら 3 つの時点での患者の平均残り心拍数に有意差があるかどうかを確認できます。
2. 3 つの異なる条件で被験者の平均スコアを測定します。
たとえば、被験者に 3 つの異なる映画を観てもらい、どれだけ気に入ったかに基づいてそれぞれを評価してもらうとします。すべてのトピックがすべてのサンプルに含まれるため、フリードマン テストを実行して、3 つの映画の平均評価に大きな違いがあるかどうかを確認できます。
フリードマン テスト: 例
3 つの異なる薬剤に対する被験者の平均反応時間が異なるかどうかを知りたいとします。これをテストするために、10 人の患者を募集し、3 つの異なる薬に対するそれぞれの反応時間 (秒単位) を測定します。各患者の結果は以下に示されています。
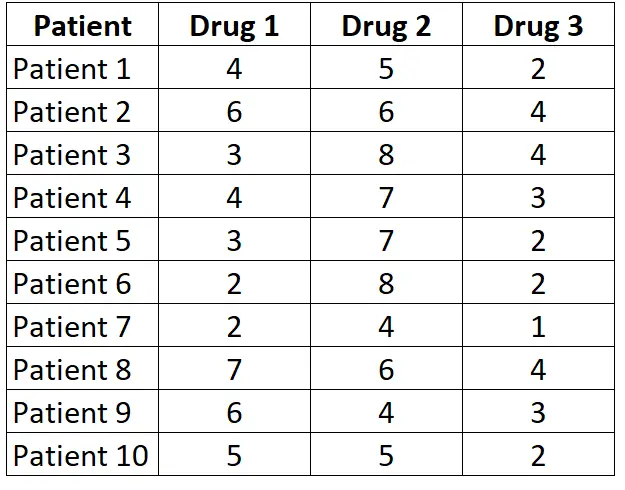
各患者は 3 つの薬剤のそれぞれについて測定されるため、フリードマン テストを使用して、3 つの薬剤間で平均反応時間が異なるかどうかを判断します。
ステップ 1. 仮説を述べます。
帰無仮説 (H 0 ): µ 1 = µ 2 = µ 3 (母集団全体の平均反応時間はすべて等しい)
対立仮説: (Ha):少なくとも 1 つの母集団平均値が残りの平均値と異なる
ステップ 2. フリードマン テストを実行します。
次の入力を使用してフリードマン テスト計算機を使用します。
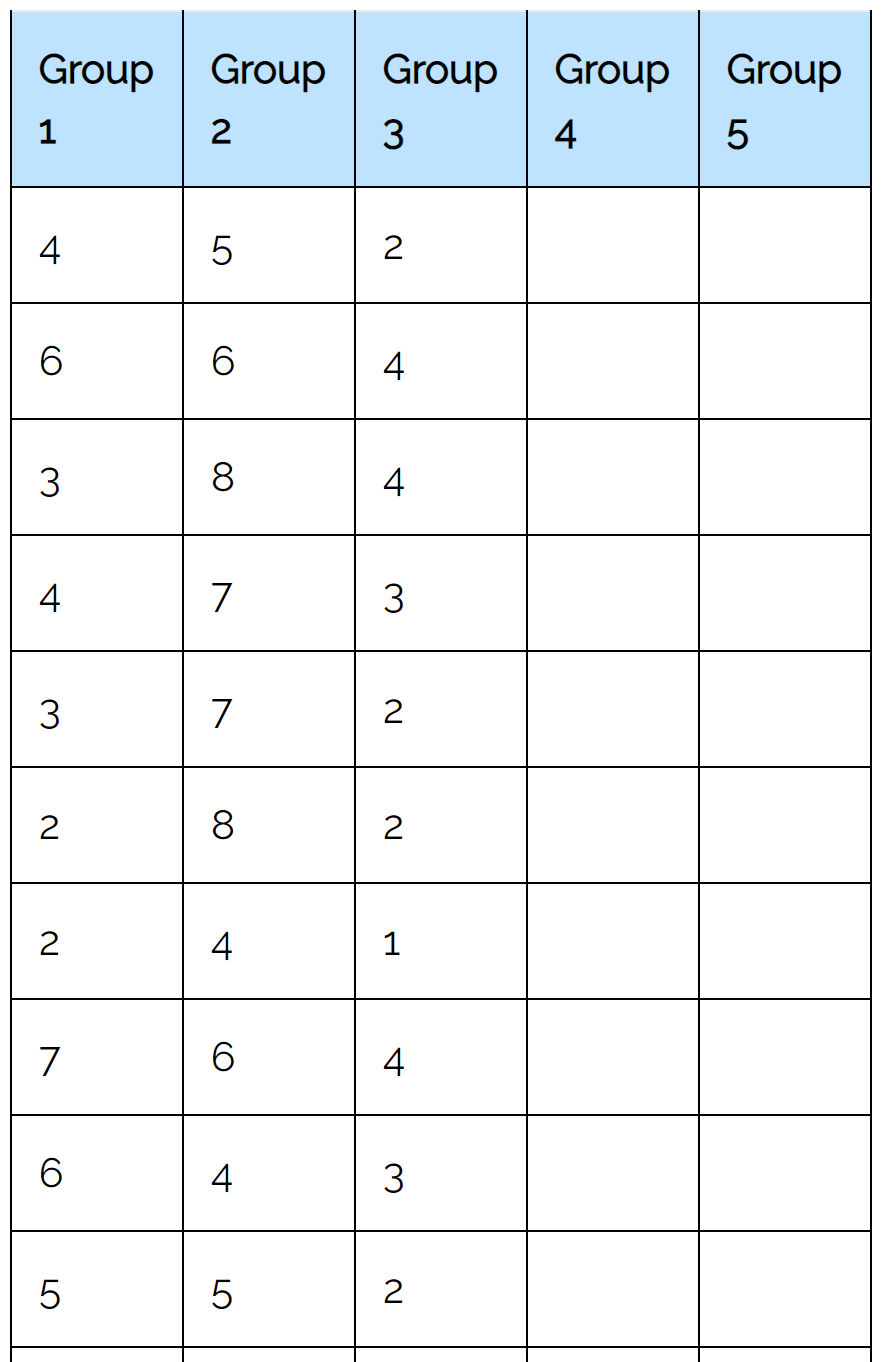
「計算」をクリックすると、次の結果が自動的に表示されます。

ステップ 3: 結果を解釈します。
検定統計量は Q = 12.35で、対応する p 値は p = 0.00208です。この値は 0.05 未満であるため、平均応答時間は 3 つの薬剤すべてで同じであるという帰無仮説を棄却できます。
私たちは、使用される薬剤の種類によって反応時間に統計的に有意な差が生じると結論付けるのに十分な証拠を持っています。
ステップ 4: 結果を報告します。
最後に実験結果を報告したいと思います。これを行う方法の例を次に示します。
反応時間に対する 3 つの異なる薬剤の影響を調べるために、10 人の患者に対してフリードマン テストが実施されました。各患者は各薬剤を 1 回ずつ使用しました。
結果は、使用された薬剤の種類によって反応時間に統計的に有意な差が生じることが示されました (Q = 12.35、p = 0.00208)。
追加リソース
次のチュートリアルでは、さまざまな統計ソフトウェアを使用してフリードマン テストを実行する方法を説明します。
Excel でフリードマン テストを実行する方法
R でフリードマン テストを実行する方法
Python でフリードマン テストを実行する方法
Stata でフリードマン テストを実行する方法
オンライン フリードマン テスト電卓