ベイズの定理
この記事では、ベイズの定理とは何なのか、確率や統計でどのように使用されるのかについて説明します。したがって、ベイズの定理の公式とは何か、ベイズの定理の解決例、およびこの定理の応用は何かを発見します。
ベイズの定理とは何ですか?
確率論では、ベイズの定理は、イベントに関する先験的な情報がわかっている場合に、そのイベントの確率を計算するために使用される法則です。
より具体的には、ベイズの定理は、イベント B が与えられた場合のイベント A の確率と、A が与えられた場合の B の確率とを数学的に関連付けます。
たとえば、インフルエンザに罹患したときに頭痛が起こる確率が事前にわかっている場合、ベイズの定理を使用して、頭痛が発生したときにインフルエンザに罹患する確率を求めることができます。
ベイズの定理には多くの応用例があり、たとえば、他の事象によって条件付けられる特定の事象の確率を計算するために、医学、経済学、またはテクノロジーで使用されます。以下では、ベイズの定理のさまざまな応用について詳しく説明します。
ベイズの定理はイギリスの数学者トーマス ベイズ (1702-1761) によって発明されましたが、発表されたのは死後の 1763 年です。
ベイズの定理の公式
ベイズの定理によれば、確率がゼロではない相互に排他的なイベントのセット {A 1 , A 2 ,…, A i ,…, A n } と別のイベント B で構成されるサンプル空間が与えられると、条件式を数学的に関連付けることができます。イベント B が与えられた場合の A i の確率と、A iが与えられた場合の B の条件付き確率。
したがって、ベイズの定理(ベイズの法則とも呼ばれます) の公式は次のとおりです。

金:
-
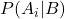
は、事後確率と呼ばれる、イベント B が与えられた場合のイベント A の条件付き確率です。
-

は、イベント A iが与えられた場合のイベント B の条件付き確率です。
-

はイベント A iが発生する確率であり、アプリオリ確率と呼ばれます。
ベイズの定理公式の分母はイベント B の合計確率であることに注意してください。
ベイズの定理の例
ベイズ定理の定義とその公式が何であるかを理解したら、概念をよりよく理解するためにベイズ定理を使用して確率を計算する方法の解決例を見てみましょう。
- 家電量販店では、X、Y、Z の 3 つのブランドのテレビを販売しています。売上の 20% は欠陥のあるブランドのテレビ、3% のブランド Y のテレビは欠陥があり、4% のブランド Z のテレビは欠陥があると推定されています。テレビに欠陥がある場合、それがブランド Z のテレビである確率はどれくらいですか?
この演習により、顧客が各ブランドのテレビを購入する確率がわかります。
- イベント A 1 : 顧客がブランド X のテレビを購入 → P(A 1 )=0.20
- イベント A 2 : 顧客がブランド Y のテレビを購入 → P(A 2 )=0.50
- イベント A 3 : 顧客がブランド Z のテレビを購入 → P(A 3 )=0.30
さらに、この読み取り値から、各ブランドのテレビに欠陥がある確率もわかります。
イベント B: テレビが故障している
- B|A 1 : ブランド X のテレビがあるとすると、そのテレビは欠陥品です → P(B|A 1 )=0.05
- B|A 2 : ブランド Y のテレビがあるとすると、そのテレビは欠陥品です → P(B|A 2 )=0.03
- B|A 3 : ブランド Z のテレビがあるとすると、そのテレビは欠陥品です → P(B|A 3 )=0.04
したがって、関心のあるすべてのイベントの確率ツリーは次のようになります。

したがって、テレビに欠陥がある場合に、それがブランド Z である確率を計算するには、ベイズの定理の式を使用する必要があります。

この例で使用されている用語を使用すると、ベイズの公式は次のようになります。
![]()
したがって、特定の欠陥のあるテレビがブランド Z である確率の計算は次のようになります。
![Rendered by QuickLaTeX.com \begin{aligned}P(A_3|B)&=\cfrac{P(B|A_3)\cdot P(A_3)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)+ P(B|A_3)\cdot P(A_3)}\\[2ex]&=\cfrac{0,04\cdot 0,30}{0,05\cdot 0,20+0,03\cdot 0,50+0,04\cdot 0,30}\\[2ex]&=0,32\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-818d0f3336f855a1315d6a94f01d1876_l3.png)
結論として、テレビに欠陥がある場合、それがブランド Z である確率は 32% です。
ベイズの定理の応用
ベイズの定理には次のような多くの応用例があります。
- 医療検査: ベイズの定理は、診断検査に合格する確率を決定するために医学で頻繁に使用されます。たとえば、HIV 検査の場合、定理を使用して、検査結果が陽性の場合にその人が実際にウイルスに感染している確率を計算できます。
- 財務分析: ファイナンスでは、ベイズの定理を使用して、一連の経済変数が与えられた場合に、株価の増減などの特定の経済イベントが発生する確率を計算します。
- 市場調査: ベイズの定理により、たとえば、ある人がこの製品の広告を見た後にその製品を購入する確率を決定することができます。
- 天気予報: 気象モデルは、観測データに基づいて特定の天気予報が当たる確率を決定するためにベイズの定理も使用します。これにより、気候予測の精度が向上します。
- コンピューター セキュリティ– サイバーセキュリティでは、ベイズの定理を適用して、不審なアクティビティが本当にコンピューター システムへの攻撃である可能性を判断できます。
ベイズの定理の問題を解決
演習 1
人口の1%が何らかの病気を患っていると推定されています。この病気を検出するための検査は、陽性の場合は 95%、陰性の場合は 90% の精度です。無作為に選ばれた人が陽性反応を示した場合、その人が実際にその病気に罹患している確率はどれくらいでしょうか?
演習ステートメントにより、次の確率が得られます。
A 1 : その人は病気を患っています → P(A 1 )=0.01
A 2 : その人は病気を持っていません → P(A 2 )=0.99
B: 検査結果は陽性です
B|A 1 : 病気に罹患している場合、検査は陽性となる → P(B|A 1 )=0.95
B|A 2 : 病気がない場合、検査は陽性となる → P(B|A 2 )=1-0.90=0.10
次に、ランダムに選択された人が検査で陽性となったときに実際にその病気に罹患している確率を計算するには、ベイズの法則を適用する必要があります。

![]()
そこで、式に値を代入して確率計算を実行します。
![Rendered by QuickLaTeX.com \begin{aligned}P(A_1|B)&=\cfrac{P(B|A_1)\cdot P(A_1)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)}\\[2ex]&=\cfrac{0,95\cdot 0,01}{0,95\cdot 0,01+0,10\cdot 0,99}\\[2ex]&=0,0876\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-135e9ab7de6b44e7392fae0f5e70a125_l3.png)
つまり、無作為に選ばれた人が検査で陽性反応を示し、実際に病気に罹患している確率は8.76%ということになる。
演習 2
株価が 1 日に上昇する確率は 40%、安定している確率は 10%、下落する確率は 50% と推定されています。さらに、市場が上昇している場合、金融アナリストが正しく予測する確率は 90% であり、市場が安定している場合、予測が正しい確率は 75%、下落した場合には、予測が当たる確率は 75% です。 85%.%。アナリストが市場が下落すると予測した場合、実際に下落する可能性はどのくらいですか?
この場合、演習ステートメントは次の確率を提供します。
A 1 : 市場は 1 日で上昇 → P(A 1 )=0.40
A 2 : 市場は 1 日にわたって安定 → P(A 2 )=0.10
A 3 : 市場は 1 日で上昇 → P(A 3 )=0.50
B: アナリストは市場が下落すると予測しています
B|A 1 : アナリストは市場が上昇すると正しく予測 → P(B|A 1 )=0.90
B|A 2 : アナリストは市場が安定していると正しく予測 → P(B|A 2 )=0.75
B|A 3 : アナリストは市場が下落すると正確に予測 → P(B|A 3 )=0.85
アナリストが市場が下落するという予測を立て、それが正しい確率を判断するには、ベイズの定理の公式を使用する必要があります。

![]()
確率値をベイズの公式に代入して確率を計算します。
![Rendered by QuickLaTeX.com \begin{aligned}P(A_3|B)&=\cfrac{P(B|A_3)\cdot P(A_3)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)+ P(B|A_3)\cdot P(A_3)}\\[2ex]&=\cfrac{0,85\cdot 0,50}{0,90\cdot 0,40+0,75\cdot 0,10+0,85\cdot 0,50}\\[2ex]&=0,4942\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-9f98a5a8a91299aa55aab02159dcebec_l3.png)
したがって、アナリストが株式市場が下落するという発言が正しい確率は 49.42% です。