優先順位付けマトリックス (または優先順位マトリックス)

この記事では、優先度マトリックス (優先度マトリックスとも呼ばれます) とは何なのか、その特徴は何なのか、また何に使用されるのかについて説明します。同様に、優先順位付けマトリックスの作成方法と、ステップごとに説明された例を確認できます。

優先順位付けマトリックスとは何ですか?

優先順位付けマトリックス(または優先順位マトリックス) は、複数の基準に基づいてさまざまなオプションを比較できるようにするマトリックスです。そのため、優先順位付けマトリックスは、さまざまなオプションを評価し、客観的に 1 つを選択するために使用されます。

つまり、優先順位付けマトリックスでは、利用可能なさまざまなオプションが、以前に選択された基準に従って取得されたスコアに従って分類され、このようにして客観的な方法に基づいて決定を行うことができます。

通常、行列の各行は選択できるオプションであり、行列の列は選択基準を表します。したがって、行と列が交差するボックスが、この基準でこのオプションが受け取るスコアになります。

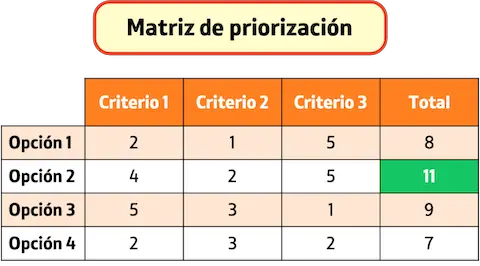
優先順位付けマトリックスは、多基準マトリックスまたは優先順位付け図とも呼ばれます。

優先順位付けマトリックスの作り方

優先順位付けマトリックスを作成する手順は次のとおりです。

1. 優先順位付けマトリックスの目的を定義する: 優先順位付けマトリックスの作成を開始する前に、マトリックス作成の目的を明確にする必要があります。こうすることで、基準を選択しやすくなります。
2. オプションを特定する: 評価する必要があるすべての可能なオプションのリストを作成します。オプションがすでに定義されている場合もありますが、機知に富んで代替案を考え出す必要がある場合もあります。
3. 基準を確立する: さまざまなオプションを採点するために選択される基準は、優先順位付けマトリックスの目的と一致している必要があります。そのため、マトリックスの目的を明確に定義することが重要です。さらに、プロジェクトに関連する基準のみを入力する必要があります。基準が多すぎると、選択されたオプションが最適ではなくなる可能性があります。
4. 基準の重み付け: さまざまな基準を定義したら、それぞれの重要性に応じて重み付けする必要があります。通常、これはパーセンテージとして行われるため、より重要な基準がより高いパーセンテージに対応し、すべての重みの合計が 1 (または 100%) になります。
5. オプションを評価する– 各オプションは、各基準のスコアを受け取る必要があります。基準の重要性の違いは重みによってすでに確立されているため、すべてのスコアの範囲を同じにすることをお勧めします。
6. 最適なオプションを選択します: 各基準のすべてのオプションを評価した後、受け取ったすべてのスコアが合計されます。理論的には、最も多くのポイントを獲得したものが最良の選択肢となります。

優先順位付けマトリックスの例

優先順位付けマトリックスの定義とその実行方法を確認した後、概念の理解を完了するための段階的な例を見ていきます。

• 銀行は、成長を目指して中小企業を買収し、より高い価格で転売することで投資をしたいと考えています。いくつかの経済フィルターを通過した後、購入を検討している企業は A 社、B 社、C 社です。

銀行にとってどの企業を買収するのが最適かを分析するために、優先順位マトリックスを作成します。この場合、マトリックスの目的とさまざまなオプションはすでにわかっています。

目的:中小企業を買収して、しばらくしてからより多くのお金で転売し、投資を収益化します。

可能性:

• オプション 1: A 社
• オプション 2: B 社
• オプション 3: C 社

さまざまなオプションを評価するために、次の選択基準を使用します。

基準：

• 基準 1: 購入価格。論理的には、企業の買収価格が低ければ低いほど、支出される資金が減り、銀行の利益が大きくなります。
• 基準 2: 成長の可能性。銀行はより大きな経済的利益を得ることができるため、企業の成長と価値の増加の可能性を考慮する必要があります。
• 基準 3: 破産のリスク。また、各企業が破産に陥るリスクも考慮する必要があります。この場合、銀行は投資した資金をすべて失うことになるからです。この基準のスコアが高いほど、会社が閉鎖されるリスクは低くなります。
• 基準 4: 会社の年間利益。会社の年間利益も評価する必要があります。これは、会社の売買による利益とは別に銀行が得る追加のお金であるためです。

優先順位付けマトリックスで使用する基準がわかったので、それらの関連性に応じて重み付けを行います。

基準の重み付け:

• 基準 1: 購入価格→ 30%
• 基準 2: 成長の可能性→ 40%
• 基準 3: 破産のリスク→ 20%
• 基準 4: 会社の年間利益→ 10%

基準の重み付けが完了したら、評価による優先順位付けマトリックスを準備します。これを行うために、各オプションを基準ごとに 1 ～ 10 で評価し、基準の重み付けに従ってスコアを追加しました。

オプションを評価して、最適なものを選択します。

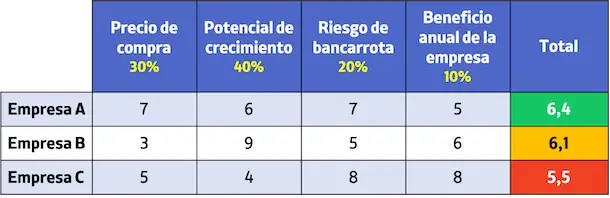
結論として、確立されたさまざまな基準に従って各企業を評価した後、最高のスコアを獲得した企業である A 社を銀行は買収する必要があります。

優先順位付けマトリックスは何に使用されますか?

以下に、優先順位付けマトリックスが何に役立つのか、またいつ使用できるのかをまとめます。

• 意思決定基準を特定する– 選択基準を特定すると、プロジェクトにとって何が最も重要で、何に基づいて意思決定を行う必要があるのかがわかります。
• 問題の明確化: 意思決定基準を選択すると、直面している実際の問題と、それを解決するための最も重要な側面をより明確に把握できます。
• オプションの分析: 優先順位付けマトリックスにより、各基準における各オプションのスコアを迅速に視覚化できるため、すべてのオプションの分析が容易になります。
• 改善の機会を探す: 優先順位付けマトリックスを実行するとき、プロジェクトにとって 1 つのオプションが最適であると結論付けることも、逆に、マトリックスで得られた結果を改善する新しいオプションを検討する必要があると結論付けることもできます。

優先順位付けマトリックスの利点と欠点

アドバンテージ：

• 優先順位付けマトリックスは使いやすいツールです。さらに、オプション、基準、または重み付けを迅速に更新および変更できます。
• 複数のオプションを分析し、どれが最適かを決定して時間を節約できるため、プロジェクト管理に非常に役立ちます。
• これは客観的な方法なので、人が抱く偏見は軽減されます。
• 優先順位付けマトリックスは、それを実行する人にとっても、それを解釈する人にとっても非常に理解しやすいものです。

短所:

• 得られる結果は基準とその重み付けの自己評価に完全に依存するため、チームは中立を保つ必要があります。
• 組織の種類によっては、優先順位付けのマトリックスが厳格になりすぎる場合があります。
• 場合によっては、2 つ以上のオプションのスコアが非常に似ているため、どの決定を下すべきかが不明確になることがあります。この場合、他の基準と重みを使用して優先度マトリックスをやり直すことをお勧めします。