確率変数とは何ですか?
一般に X で示されるランダム変数は、ランダム プロセスの結果として取り得る値を持つ変数です。
確率変数には、離散変数と連続変数の 2 種類があります。
離散確率変数
離散確率変数とは、0、1、2、3、4、5…100、100万などの可算数の個別の値のみを取ることができる変数です。離散確率変数の例をいくつか示します。
- コインを 20 回投げた後に裏が出た回数。
- サイコロを 100 回振った後に4 の目が出た回数。
- 50 個のウィジェットが入ったボックス内の欠陥のあるウィジェットの数。
離散確率変数の確率分布は、その確率変数が特定の値を取る確率を示します。
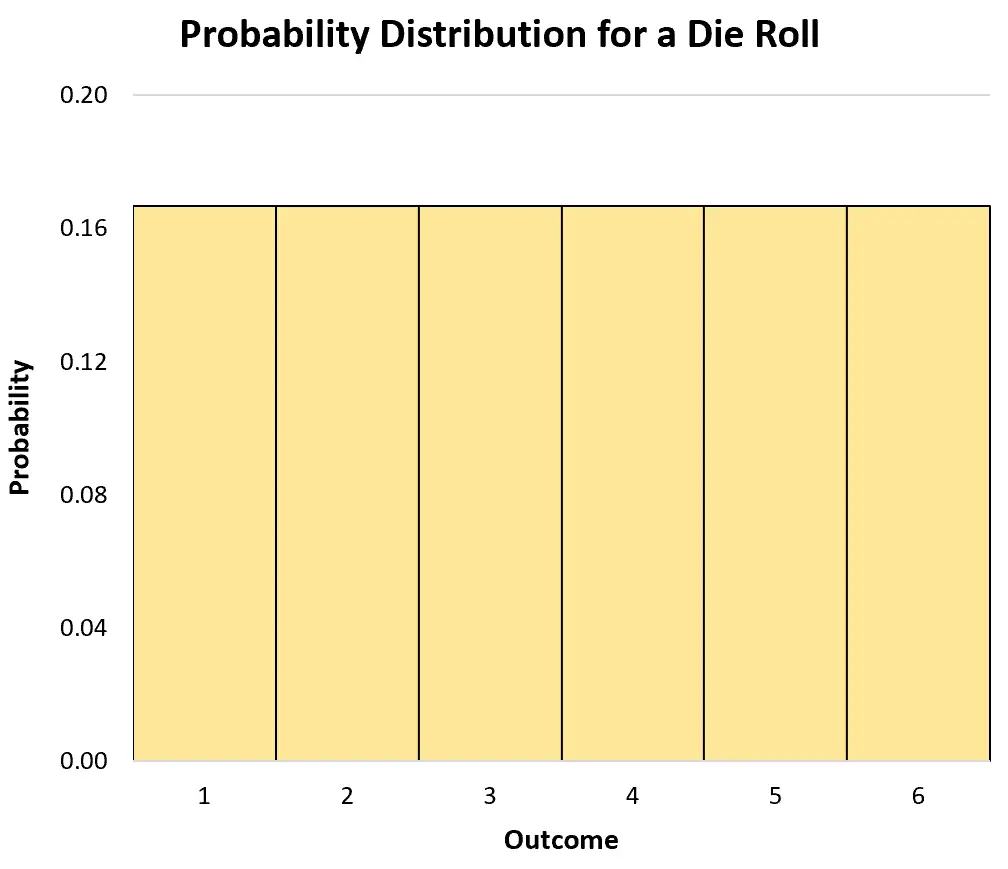
たとえば、公平なサイコロを 1 回振ったとします。サイコロが特定の数字に当たる確率を X とすると、確率分布は次のように書くことができます。
- P(X=1): 1/6
- P(X=2): 1/6
- P(X=3): 1/6
- P(X=4): 1/6
- P(X=5): 1/6
- P(X=6): 1/6
注記:
確率分布が有効であるためには、次の 2 つの基準を満たしている必要があります。
1.各結果の確率は 0 から 1 の間でなければなりません。
2.すべての確率の合計は 1 になる必要があります。
サイコロの目の確率分布は次の両方の基準を満たしていることに注意してください。
1.各結果の確率は 0 ~ 1 です。
2.すべての確率の合計は 1 になります。
ヒストグラムを使用して確率分布を視覚化できます。
離散確率変数の累積確率分布は、変数が特定の値以下の値をとる確率を示します。
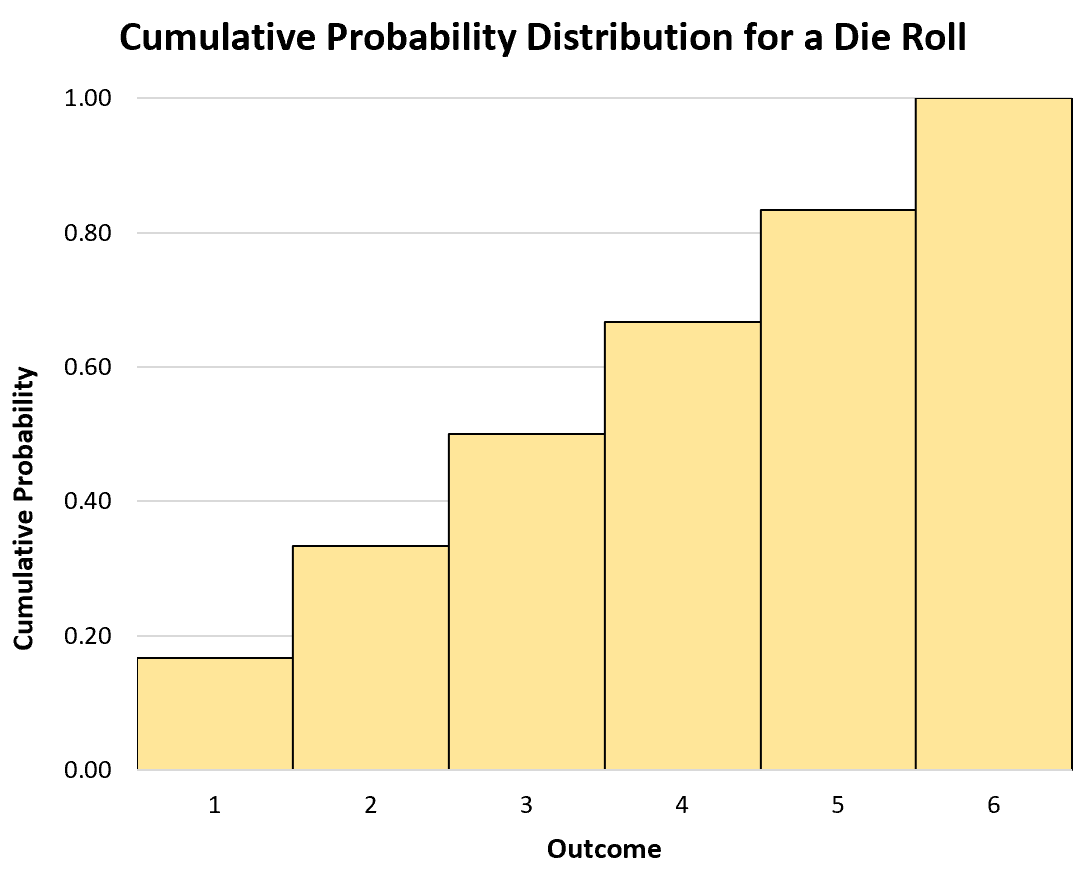
たとえば、サイコロの目の累積確率分布は次のようになります。
- P(X≤1): 1/6
- P(X≤2): 2/6
- P(X≤3): 3/6
- P(X≤4): 4/6
- P(X≤5): 5/6
- P(X≤6): 6/6
ダイスが 1 未満の数字に当たる確率は、単純に 1/6 です。1 未満の数字に当たることはありません。
2 つ以下に着地する確率は、P(X=1) + P(X=2) = 1/6 + 1/6 = 2/6 です。
同様に、3 つ以下に着地する確率は P(X=1) + P(X=2) + P(X=3) = 1/6 + 1/6 + 1/6 = 3/6 となります。すぐ。
ヒストグラムを使用して累積確率分布を視覚化することもできます。
連続確率変数
連続確率変数は、無限に多くの可能な値を取ることができる変数です。連続確率変数の例をいくつか示します。
- 動物の体重
- 人の身長
- マラソンを走るのに必要な時間
たとえば、人の身長は 60.2 インチ、65.2344 インチ、70.431222 インチなどになります。サイズの可能な値は無限にあります。
原則:
結果の数を数えることができる場合は、離散確率変数を操作していることになります。たとえば、コインが表になった回数を数えることになります。
しかし、結果を測定できれば、連続確率変数を扱うことになります (たとえば、身長、体重、時間などを測定するなど)。
連続確率変数の確率分布は、確率変数が特定の値を取る確率を示します。
ただし、離散確率変数の確率分布とは異なり、連続確率変数の確率分布は、変数が値の範囲を取る確率を知るためにのみ使用できます。
たとえば、特定のレストランのハンバーガーの重さが 4 分の 1 ポンド (0.25 ポンド) である確率を知りたいとします。重みは連続変数であるため、無限の数の値を取ることができます。
たとえば、特定のハンバーガーの実際の重さは、0.250001 ポンド、0.24 ポンド、または 0.2488 ポンドである可能性があります。特定のハンバーガーの重さがちょうど 0.25 ポンドになる確率は、本質的にはゼロです。
したがって、ハンバーガーの重さが 0.25 ポンド未満、0.25 ポンドを超える、または特定の範囲内 (たとえば、0.23 ポンドと 0.27 ポンドの間) である確率を知るには、確率分布を使用することしかできません。
追加リソース
次のチュートリアルでは、確率変数に関する追加情報を提供します。