リッジ＆なげなわ回帰を使用する場合
通常の重線形回帰では、 p 個の予測子変数のセットと応答変数を使用して、次の形式のモデルを近似します。
Y = β 0 + β 1 X 1 + β 2 X 2 + … + β p
β 0 、β 1 、B 2 、…、β pの値は、残差の二乗和 (RSS) を最小化する最小二乗法を使用して選択されます。
RSS = Σ(y i – ŷ i ) 2
金：
- Σ ：「和」を意味する記号
- y i : i 番目の観測値の実際の応答値
- ŷ i : i番目の観測値の予測応答値
回帰における多重共線性の問題
実際の重線形回帰でよく発生する問題は、 多重共線性です。これは、2 つ以上の予測変数が相互に高度に相関しており、回帰モデル内で固有の情報や独立した情報が提供されない場合です。
これにより、モデルの係数推定の信頼性が低くなり、大きな分散が示される可能性があります。つまり、モデルがこれまでに見たことのない新しいデータセットに適用されると、パフォーマンスが低下する可能性があります。
多重共線性の回避: Ridge & Lasso 回帰
この多重共線性の問題を回避するために使用できる 2 つの方法は、リッジ回帰とラッソ回帰です。
リッジ回帰では、以下を最小限に抑えようとします。
- RSS + λΣβ j 2
ラッソ回帰では、以下を最小限に抑えようとします。
- RSS + λΣ|β j |
両方の方程式において、第 2 項は撤退ペナルティと呼ばれます。
λ = 0 の場合、このペナルティ項は効果がなく、リッジ回帰とラッソ回帰は最小二乗法と同じ係数推定値を生成します。
ただし、λ が無限大に近づくにつれて、収縮ペナルティの影響が大きくなり、モデルにインポートできない予測変数はゼロに向かって減少します。
ラッソ回帰では、λ が十分に大きくなると、一部の係数が完全にゼロになる可能性があります。
リッジ＆なげなわ回帰の長所と短所
最小二乗回帰に対するリッジ回帰とラッソ回帰の利点は、 バイアスと分散のトレードオフです。
平均二乗誤差 (MSE) は特定のモデルの精度を測定するために使用できるメトリクスであり、次のように計算されることを思い出してください。
MSE = Var( f̂( x 0 )) + [バイアス( f̂( x 0 ))] 2 + Var(ε)
MSE = 分散 + バイアス2 + 既約誤差
リッジ回帰とラッソ回帰の基本的な考え方は、小さなバイアスを導入して分散を大幅に低減し、全体的な MSE を下げることです。
これを説明するために、次のグラフを考えてみましょう。
λ が増加すると、バイアスがわずかに増加するだけで分散が大幅に減少することに注意してください。ただし、ある点を超えると、分散の減少速度が鈍くなり、係数の減少により係数が大幅に過小評価され、バイアスが急激に増加します。
グラフから、バイアスと分散の間の最適なトレードオフを生み出す λ の値を選択すると、テストの MSE が最も低くなることがわかります。
λ = 0 の場合、ラッソ回帰のペナルティ項は効果がないため、最小二乗法と同じ係数推定値が生成されます。ただし、λ を特定の点まで増やすことによって、テスト全体の MSE を減らすことができます。
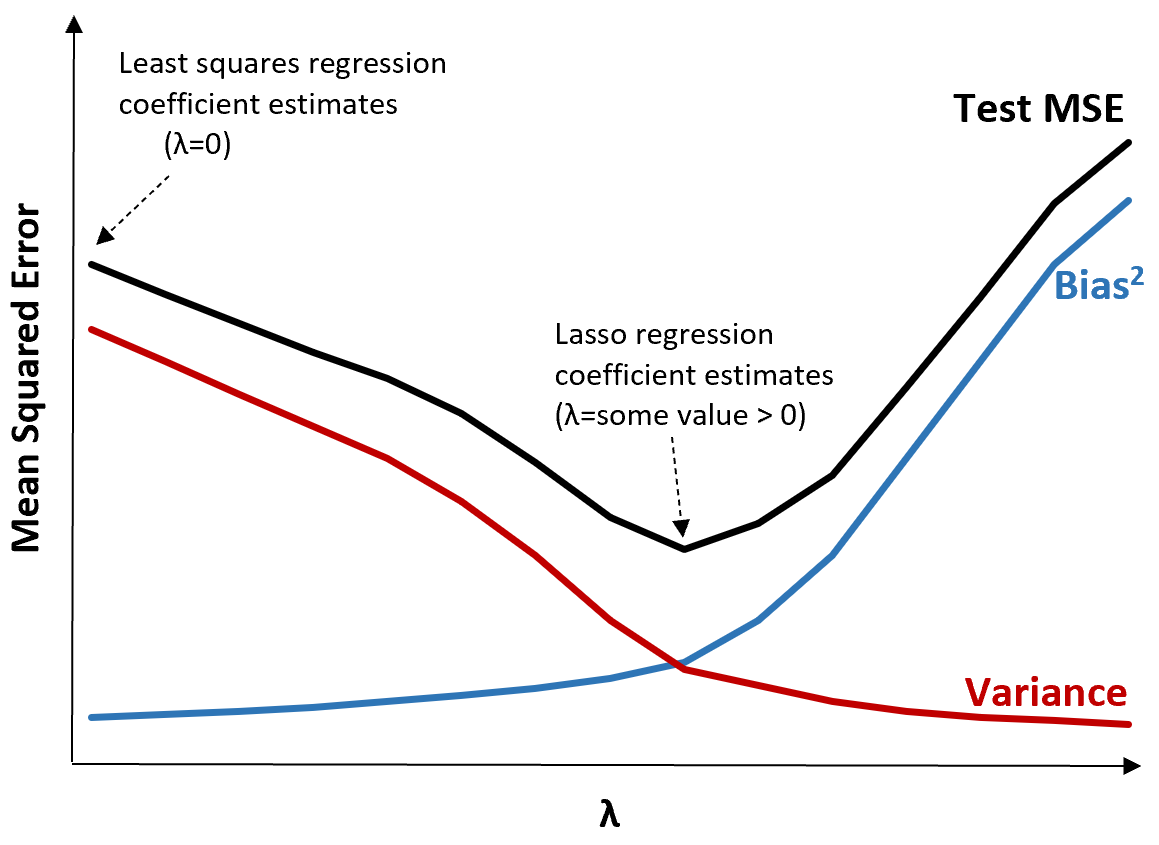
これは、リッジ回帰となげなわ回帰によるモデル フィッティングの方が、最小二乗回帰によるモデル フィッティングよりも小さなテスト エラーが生成される可能性があることを意味します。
Ridge および Lasso 回帰の欠点は、最終モデルの係数がゼロに向かって縮小するため、その係数を解釈することが難しくなることです。
したがって、リッジ回帰とラッソ回帰は、推論ではなく予測能力を最適化したい場合に使用する必要があります。
リッジ vs.ラッソ回帰: それぞれをいつ使用するか
ラッソ回帰とリッジ回帰は、両方とも残差二乗和 (RSS) と特定のペナルティ項を最小化しようとするため、正則化手法として知られています。
言い換えれば、モデル係数の推定値を制約または正規化します。
これにより、当然のことながら、リッジ回帰となげなわ回帰のどちらが優れているのかという疑問が生じます。
少数の予測子変数のみが重要である場合、ラッソ回帰は重要でない変数を完全にゼロにしてモデルから削除できるため、より適切に機能する傾向があります。
ただし、多くの予測子変数がモデル内で重要であり、それらの係数がほぼ等しい場合は、すべての予測子をモデル内に保持するため、リッジ回帰がより適切に機能する傾向があります。
予測を行うのに最適なモデルを決定するには、通常、k 分割相互検証を実行し、最小の検定二乗平均平方根誤差を生成するモデルを選択します。
追加リソース
次のチュートリアルでは、リッジ回帰とラッソ回帰の概要を説明します。
次のチュートリアルでは、R と Python で両方のタイプの回帰を実行する方法について説明します。
著者について
ベンジャミン・アンダーソン博士
私はベンジャミンです。退職した統計教授から、専任の Statorials 教育者になりました。 統計分野における豊富な経験と専門知識を活かして、私は Statorials を通じて学生に力を与えるために自分の知識を共有することに尽力しています。もっと知る