ワイブル分布
この記事では、ワイブル分布とは何か、またその用途について説明します。さらに、ワイブル分布のグラフ表現と、このタイプの確率分布の特性を確認することができます。
ワイブル分布とは何ですか?
ワイブル分布は、形状パラメーター α とスケール パラメーター λ の 2 つの特性パラメーターによって定義される連続確率分布です。
統計学では、ワイブル分布は主に生存分析に使用されます。同様に、ワイブル分布にはさまざまな分野で多くの応用例があります。以下でワイブル分布の使用について詳しく説明します。
![]()
著者らによると、ワイブル分布は 3 つのパラメータでパラメータ化することもできます。次に、分布グラフが始まる横座標を示す、しきい値と呼ばれる 3 番目のパラメーターが追加されます。
ワイブル分布は、1951 年に詳細に説明したスウェーデン人のワロッディ ワイブルにちなんで命名されました。ただし、ワイブル分布は 1927 年にモーリス フレシェによって発見され、1933 年にロジンとラムラーによって初めて適用されました。
ワイブル分布のプロット
ワイブル分布の定義を理解したら、パラメータの値に応じてそのグラフ表現がどのように変化するかがわかります。
以下に、ワイブル分布の密度関数グラフが形状パラメーターとスケール パラメーターの値に応じてどのように変化するかを示すいくつかの例を示します。
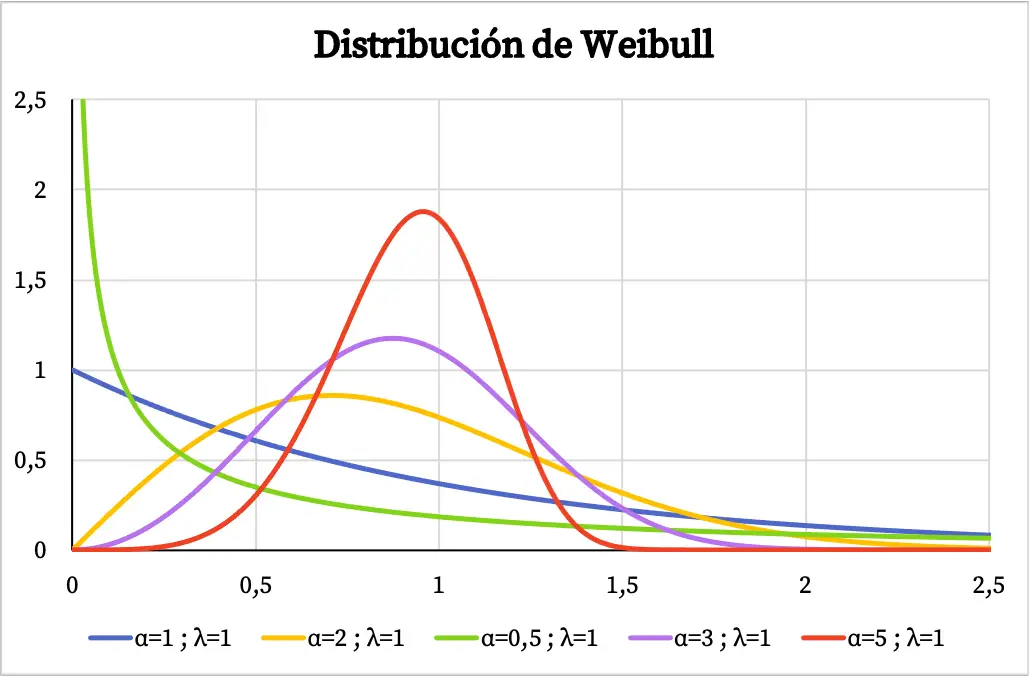
ワイブル分布を使用してシステムの故障率を時間の関数としてモデル化する場合、形状パラメータ α の値は次のことを意味します。
- α<1: 故障率は時間の経過とともに減少します。
- α=1: 故障率は時間の経過とともに一定です。
- α>1: 時間の経過とともに故障率が増加します。
一方、次のグラフでは、特性値に基づいてプロットされたワイブル分布の累積確率関数を確認できます。
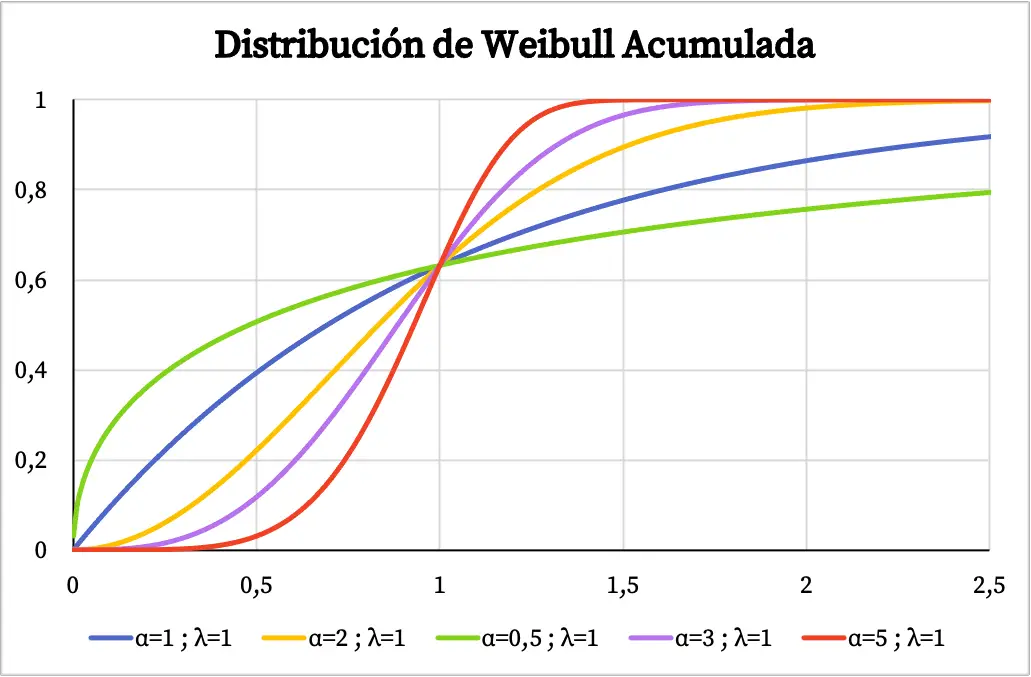
ワイブル分布の特徴
ワイブル分布には次の特徴があります。
- ワイブル分布には、そのグラフを定義する 2 つの特徴的なパラメーター、形状パラメーター α とスケール パラメーター λ があります。どちらのパラメータも正の実数です。
![\begin{array}{c}\alpha >0\\[2ex]\lambda >0\\[2ex]\text{Weibull}(\alpha,\lambda)\end{array}” title=”Rendered by QuickLaTeX.com” height=”92″ width=”101″ style=”vertical-align: 0px;”></p>
</p>
<ul>
<li>ワイブル分布は正の横座標値のみを受け入れます。</li>
</ul>
<p class=](https://statorials.org/wp-content/ql-cache/quicklatex.com-c8794febbd607514546841a325490654_l3.png)
![]()
- ワイブル分布の平均は、次の式で計算されます。
![]()
- 一方、ワイブル分布の分散を求める公式は次のとおりです。
![]()
- α>1 のワイブル分布に従う確率変数の最頻値は、次の式で決定できます。
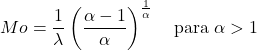
![]()
- 同様に、ワイブル分布の累積確率関数の式は次のとおりです。
![]()
- ワイブル分布の非対称係数は、次の式を適用して計算されます。
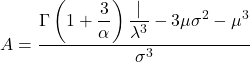
- 最後に、ワイブル分布の尖度係数を決定できる式は次のとおりです。
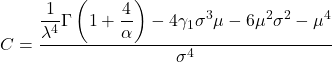
金
![]()
ワイブル分布の応用
ワイブル分布には次のような多くの用途があります。
- 応用統計では、生存分析にワイブル分布が使用されます。
- エンジニアリングでは、製造時間に関連する関数をモデル化するためにワイブル分布が使用されます。
- レーダー システムにおいて、受信信号の分散をシミュレートします。
- 保険分野では、保険金請求の範囲をモデル化します。
- たとえば、気象学では、さまざまな風速の頻度をモデル化します。