一元配置分散分析: 定義、公式、および例
一元配置 ANOVA (「分散分析」) は、3 つ以上の独立したグループの平均を比較し、対応する母集団の平均間に統計的に有意な差があるかどうかを判断します。
このチュートリアルでは次について説明します。
- 一元配置分散分析を実行する動機。
- 一元配置分散分析を実行するために満たさなければならない仮定。
- 一元配置分散分析を実行するプロセス。
- 一元配置分散分析を実行する方法の例。
一元配置分散分析: モチベーション
3 つの異なるテスト準備プログラムが大学入学試験の平均点の違いにつながるかどうかを知りたいとします。全国には何百万人もの高校生がいるのですから、すべての生徒を訪ねて試験対策プログラムを利用させるのは時間も費用もかかりすぎます。
代わりに、母集団から 100 人の学生からなる3 つの ランダムなサンプルを選択し、各サンプルが 3 つの試験準備プログラムのいずれかを使用して試験の準備をできるようにすることができます。そうすれば、各生徒が試験を受けると、その得点を記録できるようになります。
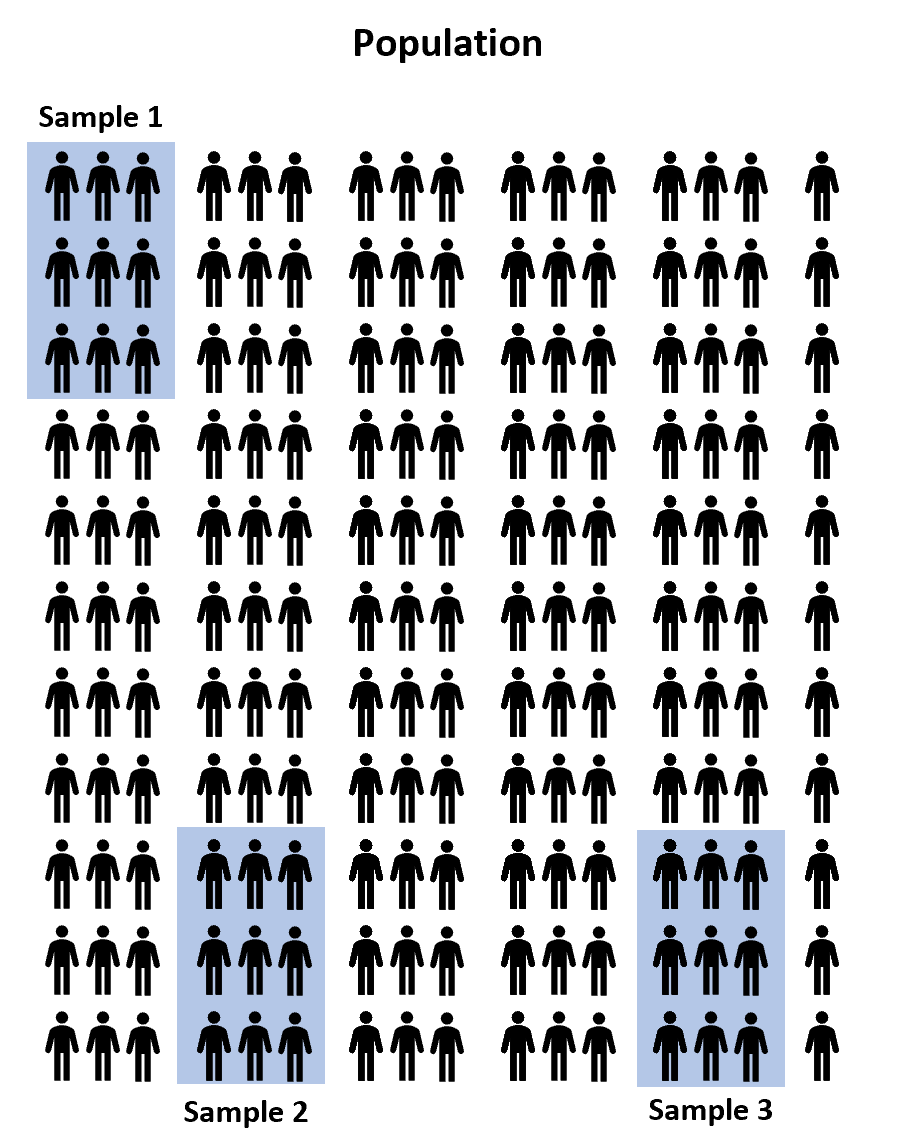
ただし、3 つのサンプル間の試験の平均点が少なくとも少し異なることが事実上保証されています。問題は、この差が統計的に有意であるかどうかです。幸いなことに、一元配置分散分析により、この質問に答えることができます。
一元配置分散分析: 仮定
一元配置 ANOVA の結果が有効であるためには、次の前提を満たす必要があります。
1. 正規性– 各サンプルは正規分布した母集団から抽出されました。
2. 等しい分散– サンプルが抽出された母集団の分散は等しい。 バートレットの検定を使用して、この仮説を検証できます。
3. 独立性– 各グループ内の観測値は互いに独立しており、グループ内の観測値はランダムサンプリングによって取得されました。
これらの仮定を検証する方法の詳細については、この記事をお読みください。
一元配置分散分析: プロセス
一元配置分散分析では、次の帰無仮説と対立仮説が使用されます。
- H 0 (帰無仮説): μ 1 = μ 2 = μ 3 = … = μ k (すべての母集団平均は等しい)
- H 1 (対立仮説):少なくとも 1 つの母集団平均が異なる 休む
一元配置分散分析を手動で実行するのは面倒なため、通常は何らかの統計ソフトウェア (R、Excel、Stata、SPSS など) を使用して一元配置分散分析を実行します。
使用するソフトウェアに関係なく、次の表が出力として表示されます。
| ソース | 二乗和 (SS) | DF | 平均二乗 (MS) | F | p |
|---|---|---|---|---|---|
| 処理 | RSS | DF R | MSR | MSR/MSE | F df r 、 df e |
| エラー | ESS | DF e | MSE | ||
| 合計 | OHS | DF T |
金:
- SSR:二乗和回帰
- SSE:二乗誤差の合計
- SST:総二乗和 (SST = SSR + SSE)
- df r :回帰自由度 (df r = k-1)
- df e :誤差自由度 (df e = nk)
- df t :合計自由度 (df t = n-1)
- k:グループの総数
- n:観測値の合計
- MSR:平均二乗回帰 (MSR = SSR/df r )
- MSE:平均二乗誤差 (MSE = SSE/df e )
- F: F 検定統計量 (F = MSR/MSE)
- p: F dfr, dfeに対応する値 p
p 値が選択した有意水準 (0.05 など) より小さい場合は、帰無仮説を棄却し、母集団平均の少なくとも 1 つが他の平均とは異なると結論付けることができます。
注:帰無仮説を棄却した場合、母集団平均の少なくとも 1 つが他の平均と異なることを示しますが、ANOVA 表ではどの母平均が異なるかは指定されません。これを判断するには、「多重比較」テストとも呼ばれる事後テストを実行する必要があります。
一元配置分散分析: 例
3 つの異なる試験準備プログラムが、特定の試験で異なる平均点につながるかどうかを知りたいとします。これをテストするために、研究に参加する 30 人の学生を募集し、3 つのグループに分けます。
各グループの学生は、次の 3 週間、3 つの試験準備プログラムのうち 1 つを使用して試験の準備をするようにランダムに割り当てられます。 3 週間の終わりに、生徒全員が同じ試験を受けます。
各グループの試験結果は以下のとおりです。

このデータに対して一元配置分散分析を実行するには、次の入力を使用して 統計の一元配置分散分析計算機を使用します。

出力テーブルから、F 検定統計量が2.358で、対応する p 値が0.11385であることがわかります。

この p 値は 0.05 未満ではないため、帰無仮説を棄却できません。
これは、 3 つのグループの平均試験得点の間に統計的に有意な差があると言える十分な証拠がないことを意味します。
追加リソース
次の記事では、さまざまな統計ソフトウェアを使用して一元配置分散分析を実行する方法について説明します。
Excel で一元配置分散分析を実行する方法
R で一元配置分散分析を実行する方法
Python で一元配置分散分析を実行する方法
SAS で一元配置分散分析を実行する方法
SPSS で一元配置分散分析を実行する方法
Stata で一元配置分散分析を実行する方法
TI-84 電卓で一元配置分散分析を実行する方法
オンライン一元配置分散分析計算機