統計において中央値が重要なのはなぜですか?

中央値は、すべての値を最小から最大の順に並べたときの、データ セットの中央の値を表します。

たとえば、次のデータセットの中央値は 19 です。

データセット: 3、4、11、15、19、22、23、23、26

中央値は、データセットの⁵⁰パーセンタイルも表します。つまり、データセット内の値のちょうど半分が中央値を上回っており、値の半分が中央値を下回っています。

中央値は、データセットの「中心」がどこにあるのかを知ることができるため、計算すべき重要な指標です。これにより、特定のデータセットの「典型的な」値もわかります。

たとえば、特定の都市にある 10,000 戸の異なる住宅の販売価格を含むデータセットがあるとします。

生データを何行も見る代わりに、中央値を計算して、その都市の住宅の平均販売価格をすぐに把握できます。

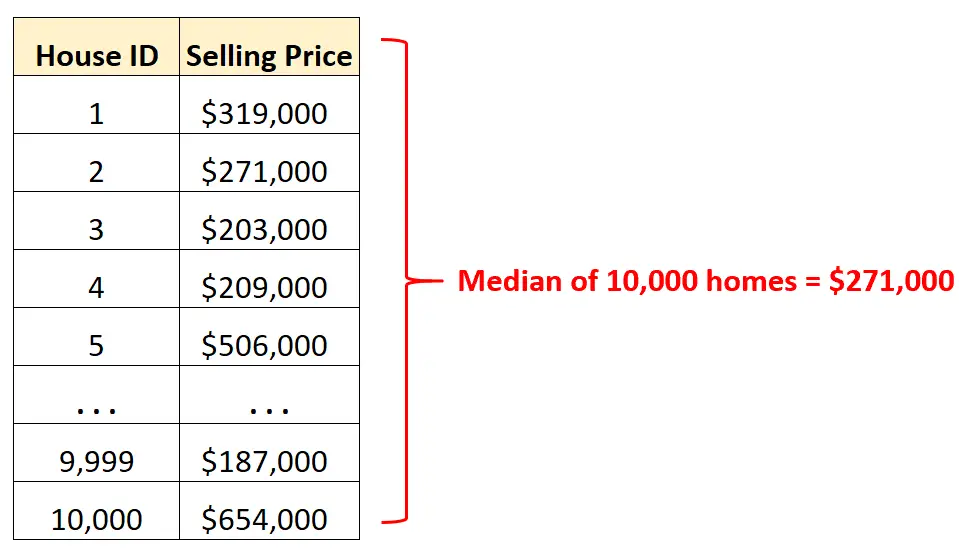
販売価格の中央値が 271,000 ドルであることがわかっているので、10,000 戸のちょうど半分がその金額を超えて販売され、残りの半分はそれ以下で販売されたことがわかります。

これにより、この都市の住宅の「典型的な」販売価格もわかります。

中央値を使用する場合

データセットを分析するとき、中心的な値がどこにあるのかを理解したいと思うことがよくあります。

統計では、データセットの中心を測定するために使用する一般的な指標が 2 つあります。

• Mean : 一連のデータの平均値
• Median : データセット内の中央値

次の状況では、中央値がより有用な尺度であることがわかります。

• 分布が非対称の場合。
• 分布に外れ値が含まれている場合。

これを説明するために、次の 2 つの例を考えてみましょう。

例 1: 偏った分布の中央値の計算

特定の都市の住民の給与の次の分布を考えてみましょう。

分布が右に偏っているため、中央値は平均よりも居住者の「典型的な」給与をよりよく反映しています。

これは、分布の右側にある賃金が高いと、平均が分布の中心から遠ざかることを意味します。

この特定の例では、平均給与は 47,000 ドルですが、中央値は 32,000 ドルです。中央値は、この都市の典型的な給与をよりよく表しています。

例 2: 外れ値が存在する場合の中央値の計算

特定の通りにある住宅の面積を示す次のグラフを考えてみましょう。

平均値は少数の非常に大きな住宅に大きく影響されますが、中央値は影響を受けません。

中央値は異常値の影響を受けないため、平均よりもその通りにある住宅の「典型的な」平方フィートをうまく捉えていることがわかります。

まとめ

この記事で取り上げる主なポイントを簡単にまとめます。

• 中央値は、データセット内の中央の値を表します。
• 中央値は、データセット内の中心値がどこにあるかを知ることができるため、重要です。
• 分布が歪んでいたり、外れ値がある場合には、平均よりも中央値の方が計算に役立つ傾向があります。

追加リソース

具体例: 平均値、中央値、最頻値の使用
平均値と平均値を使用する場合中央値: 例付き
統計において最頻値が重要なのはなぜですか?