中心的傾向の尺度: 定義と例
中心傾向の尺度は、データセットの中心点を表す単一の値です。この値は、データセットの「中心位置」とも呼ばれます。
統計では、中心傾向を示す 3 つの一般的な尺度があります。
- 平均
- 中央値
- ファッション
これらの各測定値は、さまざまな方法を使用してデータ セットの中心位置を見つけます。分析するデータの種類によっては、他の 2 つの指標ではなく、これら 3 つの指標のいずれかを使用する方がよい場合があります。
この記事では、中心傾向の 3 つの尺度をそれぞれ計算する方法と、データに基づいてどの尺度を使用するのが最適かを判断する方法について説明します。
中心傾向の測定がなぜ役立つのでしょうか?
平均値、中央値、最頻値の計算方法を説明する前に、そもそもこれらの測定値がなぜ実際に役立つのかを理解しておくと役立ちます。
次のシナリオを考えてみましょう。
若いカップルが新しい都市で最初の家をどこに買うかを決めようとしていますが、使えるのはせいぜい 15 万ドルです。市内の一部の地域には高価な家があり、ある地域には安い家があり、またある地域には中価格帯の家があります。彼らは、予算に合った特定の地域に簡単に検索を絞り込みたいと考えています。
カップルが各地域の一戸建て住宅の価格を調べただけだと、次のような結果が表示されるため、どの地域が自分たちの予算に最も適しているかを判断するのが難しいかもしれません。
近所Aの住宅価格: $140,000、$190,000、$265,000、$115,000、$270,000、$240,000、$250,000、$180,000、$160,000、$200,000、$240,000、$280,000…
近隣Bの住宅価格: $140,000、$290,000、$155,000、$165,000、$280,000、$220,000、$155,000、$185,000、$160,000、$200,000、$190,000、$140,000、$145.0 0 0、…
近隣Cの住宅価格: $140,000、$130,000、$165,000、$115,000、$170,000、$100,000、$150,000、$180,000、$190,000、$120,000、$110,000、$130,000、$120,0 0 0、…
ただし、各地域の住宅の平均価格 (中心傾向の尺度など) がわかっていれば、どの地域の住宅価格が予算に合っているかをより簡単に特定できるため、検索をより迅速に絞り込むことができます。
近隣 A の住宅の平均価格: 220,000 ドル
近隣Bの住宅の平均価格 : 190,000 ドル
近隣Cの住宅の平均価格: 140,000 ドル
各地域の平均住宅価格を知ることで、地域Cが予算内で最も多くの住宅を入手できる可能性が高いことがすぐにわかります。
これは、中心傾向の尺度を使用する利点です。これは、データ セットの中心値を理解するのに役立ち、データ値が一般的にどこにあるかを説明する傾向があります。この特定の例では、若いカップルが各地域の住宅の一般的な価格を理解するのに役立ちます。
要点:中心傾向の尺度は、データセットの「中心」を表す単一の値を提供するため便利です。これにより、データ セット内のすべての個々の値を単に調べるよりもはるかに速くデータ セットを理解することができます。
平均
中心傾向を示す最も一般的に使用される尺度は平均です。データセットの平均を計算するには、個々の値をすべて合計し、値の合計数で割るだけです。
平均 = (すべての値の合計) / (値の合計数)
たとえば、シーズン中に同じチームの 10 人の野球選手が打ったホームランの数を示す次のデータ セットがあるとします。
| プレーヤー | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #十 |
|---|---|---|---|---|---|---|---|---|---|---|
| ホームラン | 8 | 15 | 22 | 21 | 12 | 9 | 11 | 27 | 14 | 13 |
選手ごとの平均ホームラン数は次のように計算できます。
平均 = (8+15+22+21+12+9+11+27+14+13) / 10 = 15.2回路。
中央値
中央値はデータセットの中央の値です。データセット内のすべての個々の値を最小から最大の順に並べて中央値を見つけることで、中央値を見つけることができます。値の数が奇数の場合、中央値が中央の値になります。値の数が偶数の場合、中央値は中央の 2 つの値の平均です。
たとえば、前の例で 10 人の野球選手が打ったホームラン数の中央値を見つけるには、ホームラン数の降順で選手をランク付けできます。
| プレーヤー | #1 | #6 | #7 | #5 | #十 | #9 | #2 | #4 | #3 | #8 |
|---|---|---|---|---|---|---|---|---|---|---|
| ホームラン | 8 | 9 | 11 | 12 | 13 | 14 | 15 | 21 | 22 | 27 |
値の数が偶数であるため、中央値は単純に中央の 2 つの値の平均値13.5になります。
代わりに、プレイヤーが 9 人いた場合を考えてみましょう。
| プレーヤー | #1 | #6 | #7 | #5 | #9 | #2 | #4 | #3 | #8 |
|---|---|---|---|---|---|---|---|---|---|
| ホームラン | 8 | 9 | 11 | 12 | 14 | 15 | 21 | 22 | 27 |
この場合、値の数が奇数であるため、中央値は単に中央の値14になります。
ファッション
モードは、データ セット内で最も頻繁に現れる値です。データ セットには、モードがない (値が繰り返されない場合)、1 つのモード、または複数のモードを持つことができます。
たとえば、次のデータセットにはモードがありません。
| プレーヤー | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #十 |
|---|---|---|---|---|---|---|---|---|---|---|
| ホームラン | 8 | 9 | 11 | 12 | 13 | 14 | 15 | 21 | 22 | 27 |
次のデータセットにはモード15があります。これは最も頻繁に表示される値です。
| プレーヤー | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #十 |
|---|---|---|---|---|---|---|---|---|---|---|
| ホームラン | 8 | 9 | 11 | 12 | 13 | 15 | 15 | 21 | 22 | 27 |
次のデータセットには 8、15、19 の3 つのモードがあります。これらは最も頻繁に現れる値です。
| プレーヤー | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #十 |
|---|---|---|---|---|---|---|---|---|---|---|
| ホームラン | 8 | 8 | 11 | 12 | 15 | 15 | 17 | 19 | 19 | 27 |
最頻値は、どのカテゴリが最も頻繁に出現するかを示すため、カテゴリ データを扱う場合に中心傾向の尺度として特に役立ちます。たとえば、人々の好きな色に関するアンケートの結果を示す次の棒グラフについて考えてみましょう。
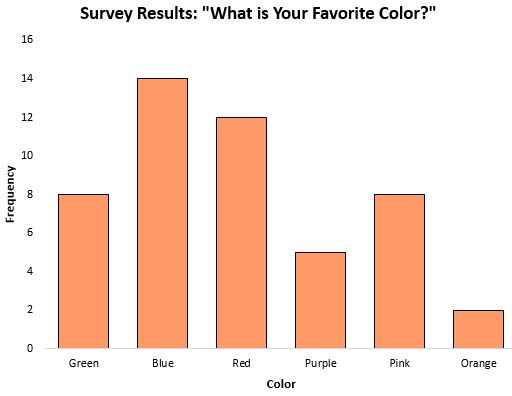
モード、または最も頻繁に発生した応答は青でした。
データがカテゴリカルであるシナリオ (上記のようなシナリオ) では、中央値や平均値を計算することさえ不可能なので、最頻値が使用できる中心傾向の唯一の尺度になります。
上の野球選手の例で見たように、このモードは数値データにも使用できます。ただし、モードは、「このデータ セットの典型的な値は何ですか?」という質問に答えるのにはあまり役に立たない傾向があります。 »
たとえば、このチームの野球選手が打った典型的なホームラン数を知りたいとします。
| プレーヤー | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #十 |
|---|---|---|---|---|---|---|---|---|---|---|
| ホームラン | 8 | 8 | 11 | 12 | 15 | 15 | 17 | 19 | 19 | 27 |
このデータセットのモードは 8、15、および 19 です。これらは最も頻繁に使用される値であるためです。ただし、これらは、チーム内の選手が打った典型的なホームラン数を理解するのにはあまり役に立ちません。この場合の中心傾向を示すより適切な尺度は、中央値 (15) または平均値 (同じく 15) です。
また、最頻値が他の値から遠く離れた数値である場合、最頻値は中心傾向の尺度としては不十分です。たとえば、次のデータセットのモードは 30 ですが、これは実際にはチームのプレーヤーごとの「典型的な」ホームラン数を表しません。
| プレーヤー | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #十 |
|---|---|---|---|---|---|---|---|---|---|---|
| ホームラン | 5 | 6 | 7 | 十 | 11 | 12 | 13 | 15 | 30 | 30 |
繰り返しますが、このデータセットの中心位置を説明するには、平均値または中央値の方が適切です。
平均値、中央値、最頻値を使用する場合
平均、中央値、および最頻値はすべて、データセットの中心位置、つまり「典型的な値」を非常に異なる方法で測定することがわかりました。
平均:データセット内の平均値を見つけます。
中央値:データセット内の中央値を検索します。
モード:データセット内の最も頻度の高い値を検索します。
以下に、中心傾向の特定の尺度が他の尺度よりも使用されるシナリオを示します。
平均を使用する場合
データ分布がかなり対称的で、外れ値がない場合は、平均を使用するのが最善です。
たとえば、特定の都市の個人の給与を示す次の分布があるとします。

この分布はかなり対称的であり (つまり、半分に分割すると、それぞれの半分はほぼ均等に見える)、外れ値がない (つまり、極端に高い給与がない) ため、平均はこのデータセットを説明するのに適しています。
平均は 63,000 ドルであることがわかり、これは分布のほぼ中心に位置します。

中央値を使用する場合
データ分布が偏っている場合、または外れ値がある場合は、中央値を使用するのが最適です。
偏ったデータ:
分布が歪んでいる場合でも、中央値はなんとか中心位置を捕捉します。たとえば、ある都市の個人の給与の次の分布を考えてみましょう。

中央値は、平均よりも個人の「典型的な」給与をよりよく反映しています。これは、分布の裾にある値が大きいと、平均が中心から離れて長い裾に向かって移動する傾向があるためです。
この特定の例では、平均値から、この都市での典型的な個人の年収は約 47,000 ドルであることがわかりますが、中央値からは、典型的な個人の年間収入はわずか 32,000 ドル程度であることがわかり、これは典型的な個人をよりよく表しています。
異常値:
中央値は、データ内に外れ値がある場合に、分布の中心位置をより適切に捕捉するのにも役立ちます。たとえば、特定の通りにある住宅の面積を示す次のグラフについて考えてみましょう。

平均値は少数の非常に大きな住宅に大きく影響されますが、中央値は影響を受けません。したがって、中央値は、平均よりも、その通りにある家の「典型的な」平方フィートをうまく捉えています。
モードを使用する場合
このモードは、カテゴリ データを操作し、どのカテゴリが最も頻繁に表示されるかを知りたい場合に最適です。ここではいくつかの例を示します。
- あなたは人々の好きな色に関するアンケートを実施しており、回答に最も頻繁に現れる色を知りたいと考えています。
- あなたは、Web サイト デザインの 3 つの選択肢の中から人々の好みに関する調査を実施しており、人々がどのデザインを最も好むかを知りたいと考えています。
前述したように、カテゴリ データを使用している場合は、中央値や平均値を計算することさえできないため、最頻値が中心傾向の唯一の尺度になります。
一般に、住宅の面積、選手ごとの本塁打数、個人ごとの給与などの数値データを扱う場合、「典型的な」値を説明するには中央値または平均を使用するのが最善です。データセット。
注:データセットが完全に正規分布している場合、平均、中央値、最頻値はすべて同じ値になることに注意することが重要です。