中心極限定理
この記事では、中心極限定理 (CLT) とは何か、また統計でどのように使用されるのかについて説明します。また、中心極限定理の公式とは何か、およびその応用例を段階的に解くこともできます。
中心極限定理とは何ですか?
統計学における中心極限定理は、中心極限定理とも呼ばれ、母集団の確率分布に関係なく、サンプルサイズが増加するにつれてサンプル平均の分布が正規分布に近づくことを示しています。
つまり、中心極限定理は、十分な数のサンプルを取得すれば、それらのサンプルの平均は正規分布に近似できるということです。
さらに、中心極限定理は、サンプルサイズが増加するにつれてサンプル平均が母集団平均の値に近づくことを示しています。これにより、統計母集団のパラメータを近似することができます。以下では、これがどのように行われるかを見ていきます。
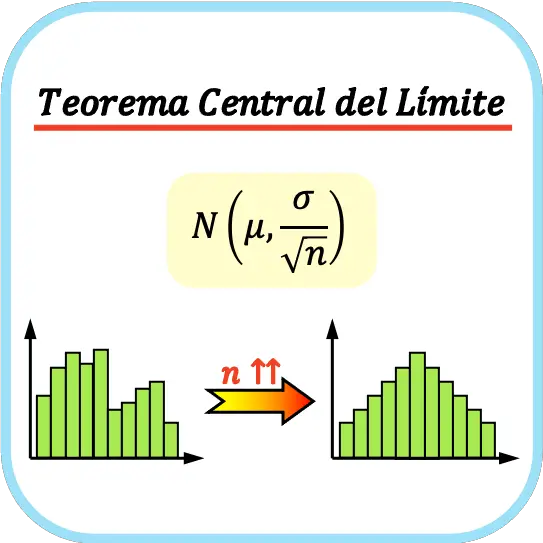
一般に、中心極限定理を適用するには、サンプルサイズは少なくとも 30 個の観測値が必要であると考えられていますが、これは研究する変数の特性によって異なります。
正規分布により仮説検定や信頼区間などの推論統計計算が可能になるため、中心極限定理には多くの用途があります。たとえば、金融では、投資のリターンとリスクを分析するために中心極限定理が使用されます。
中心極限定理の例
中心極限定理の定義を理解したら、その意味を完全に理解するために例を見てみましょう。
中心極限定理の例としては、サイコロの振りが挙げられます。すべての結果が等しい確率であるため、サイコロの目は離散一様分布に従います。ただし、いくつかの結果の合計の分布は正規分布に近づきます。
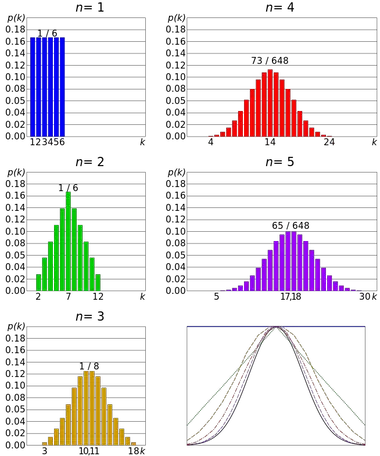
したがって、スロー数が多いほど、平均値の分布の形状が正規分布のグラフに似る可能性が高くなります。
中心極限定理の公式
中心極限定理は、母集団が平均 μ と標準偏差 σ を持ち、十分な数のサンプル (n≥30) を取得した場合、サンプル平均のセットは平均 μ と標準偏差 σ を持つ正規分布に近似できると述べています。 /√n。
![]()
さらに、 X 1の場合、次の式で定義される正規分布になります。
![]()
中心極限定理の演習を解いた
概念を完全に理解できるように、中心極限定理の解答済み演習をここに示します。
- ある会社は、特定の玩具コンポーネントを交換するために使用される部品を販売しています。コインの平均重量は 300 g、標準偏差は 50 g です。顧客が 100 個のバッチを注文した場合、バッチ内のピースの平均重量が 305 g を超える確率はどれくらいですか?また、100 個のバッチの重さが 31 kg を超える確率はどのくらいでしょうか?
バッチ サイズが大きい (n=100) ため、中心極限定理を適用して問題を解決できます。
したがって、中心極限定理の式を使用すると、次のパラメーターを使用して標本平均の分布を正規分布に近似できます。
![]()
![]()
![]()
![]()
ここで、入力プロセスを実行して、演習で要求される確率を見つけることができます。これを行うには、分布から平均を引いて、標準偏差で割る必要があります。
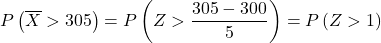 正規分布表で Z>1 がどの値に対応するかを調べる必要があります。
正規分布表で Z>1 がどの値に対応するかを調べる必要があります。
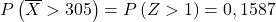
![]()
![]()
![]()
そこで、入力プロセスをやり直して、問題が尋ねる 2 番目の確率を見つけます。
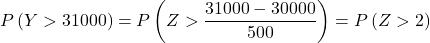
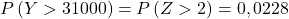 ➤参照:大数の法則
➤参照:大数の法則