統計における予測誤差とは何ですか? (定義と例)
統計学において、予測誤差とは、特定のモデルによって予測された値と実際の値との差を指します。
予測誤差は、次の 2 つの状況でよく使用されます。
1. 線形回帰:連続応答変数の値を予測するために使用されます。
通常、線形回帰モデルの予測誤差は、二乗平均平方根誤差を表すRMSEとして知られるメトリックを使用して測定されます。
次のように計算されます。
RMSE = √ Σ(ŷ i – y i ) 2 / n
金：
- Σは「和」を意味する記号です
- ŷ iは i番目の観測値の予測値です
- y iはi 番目の観測値の観測値です
- n はサンプルサイズです
2. ロジスティック回帰:バイナリ応答変数の値を予測するために使用されます。
ロジスティック回帰モデルの予測誤差を測定する一般的な方法は、合計分類誤差率として知られる指標を使用することです。
次のように計算されます。
合計誤分類率 = (誤った予測の数 / 合計の予測の数)
誤分類率の値が低いほど、モデルは応答変数の結果をより適切に予測できます。
次の例は、実際に線形回帰モデルとロジスティック回帰モデルの予測誤差を計算する方法を示しています。
例 1: 線形回帰での予測誤差の計算
回帰モデルを使用して、バスケットボールの試合で 10 人の選手が何点を獲得するかを予測するとします。
次の表は、モデルによって予測されたポイントとプレーヤーが獲得した実際のポイントを比較したものです。
二乗平均平方根誤差 (RMSE) は次のように計算します。
- RMSE = √ Σ(ŷ i – y i ) 2 / n
- RMSE = √(((14-12) 2 +(15-15) 2 +(18-20) 2 +(19-16) 2 +(25-20) 2 +(18-19) 2 +(12- 16) 2 +(12-20) 2 +(15-16) 2 +(22-16) 2 ) / 10)
- RMSE = 4
平均二乗誤差は4です。これは、予測得点と実際の得点の間の平均偏差が 4 であることを示しています。
例 2: ロジスティック回帰における予測誤差の計算
ロジスティック回帰モデルを使用して、10 人の大学バスケットボール選手が NBA にドラフトされるかどうかを予測するとします。
次の表は、各プレーヤーの予測結果と実際の結果を示しています (1 = ドラフト指名、0 = ドラフト外)。
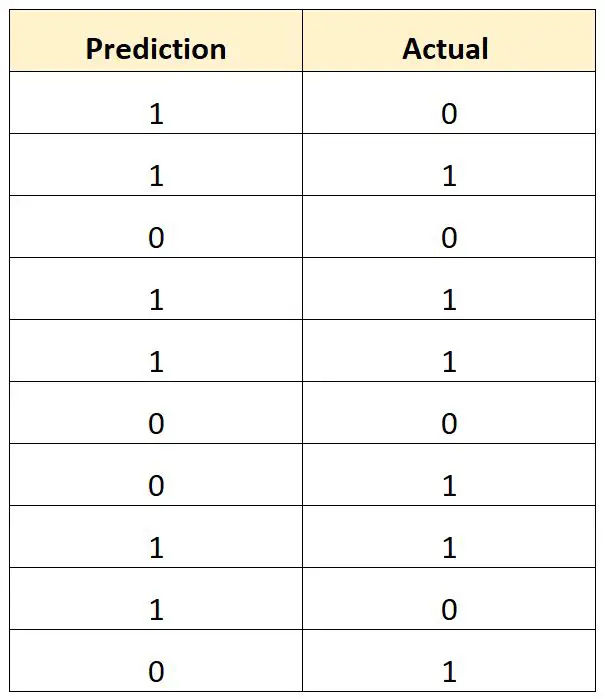
合計誤分類率は次のように計算されます。
- 合計誤分類率 = (誤った予測の数 / 合計の予測の数)
- 合計分類エラー率 = 4/10
- 合計誤分類率 = 40%
合計の分類エラー率は40%です。
この値は非常に高く、モデルが選手がドラフトされるかどうかの予測があまりうまくいっていないことを示しています。
追加リソース
次のチュートリアルでは、さまざまな種類の回帰手法について説明します。
著者について
ベンジャミン・アンダーソン博士
私はベンジャミンです。退職した統計教授から、専任の Statorials 教育者になりました。 統計分野における豊富な経験と専門知識を活かして、私は Statorials を通じて学生に力を与えるために自分の知識を共有することに尽力しています。もっと知る