事象が交差する確率

によるベンジャミン・アンダーソン博士 8月 1, 2023 確率 0コメント

この記事では、イベントの交差確率を計算する方法について説明します。したがって、イベントの交差確率の公式が何であるかを確認し、さらに、段階的に解決される演習を行います。

出来事の交差点とは何でしょうか？

確率理論では、イベントの交差はイベントの演算であり、その結果は演算のすべてのイベントに共通の基本イベントで構成されます。つまり、イベント A と B の共通部分は、同時に A と B に属するすべてのイベントによって形成されます。

2 つのイベントの交差は記号 ⋂ で表されます。したがって、イベント A と B の交差部分は A⋂B と書かれます。

たとえば、サイコロを振るランダムな実験で、偶数が出るというイベント A={2, 4, 6} と、3 より大きい数字が出るというイベント B={4, 5, 6 }、2 つのイベントの交差部分は A⋂B={4, 6} です。

イベントの交差確率の公式

2 つのイベントが交差する確率は、 1 つのイベントが発生する確率に、最初のイベントが与えられた場合にもう 1 つのイベントが発生する条件付き確率を掛けたものに等しくなります。

したがって、 2 つのイベントの交差確率の公式は、P(A⋂B)=P(A) P(B|A)=P(B) P(A|B) となります。

$P(A\cap B)=P(A)\cdot P(B|A)=P(B)\cdot P(A|B)$

金：

$A$

そして

$B$

これらは 2 つの依存イベントです。
$P(A\cap B)$

イベント A とイベント B の交差の確率です。
$P(A)$

はイベント A が発生する確率です。
$P(B|A)$

イベント A が与えられた場合にイベント B が発生する条件付き確率です。
$P(B)$

はイベント B が発生する確率です。
$P(A|B)$

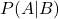
イベント B が与えられた場合にイベント A が発生する条件付き確率です。

➤参照:条件付き確率 (または条件付き確率)

ただし、2 つのイベントが独立している場合、これは、一方のイベントが発生する確率は、もう一方のイベントが発生するかどうかに依存しないことを意味します。したがって、2 つの独立したイベントの交差確率の式は次のとおりです。

$P(A\cap B)=P(A)\cdot P(B)$

金：

$A$

そして

$B$

これらは 2 つの独立したイベントです。
$P(A\cap B)$

イベント A とイベント B の交差の確率です。
$P(A)$

はイベント A が発生する確率です。
$P(B)$

はイベント B が発生する確率です。

➤参照:独立したイベント

イベント交差確率の実世界の例

次に、2 つのイベントの交差確率がどのように計算されるかを確認できるように、2 つの例を段階的に解決していきます。最初に 2 つの独立したイベントの交差の例を示し、次に 2 つの依存イベントの交差の例を見て、両方のケースを確認できるようにします。

2 つの独立したイベントの交差の確率

引き分けは 3 回連続で開始されます。 3 回のトスすべてで表になる確率を求めます。

この場合、抽選の結果は前の抽選で得られた結果に依存しないため、同時確率を計算したいイベントは独立しています。したがって、3 回連続して表が出る確率を決定するには、独立したイベントの交差確率公式を使用する必要があります。

$P(A\cap B)=P(A)\cdot P(B)$

くじを引く場合、考えられる結果は 2 つだけです。表か裏かです。したがって、コインを投げたときに表か裏が出る確率は次のようになります。

$P(\text{cara})=\cfrac{1}{2}=0,5$

したがって、3 回のコイン投げすべてで表が出る確率を求めるには、表が出る確率を 3 倍する必要があります。

$\begin{aligned}P(\text{cara}\cap \text{cara}\cap \text{cara})&=P(\text{cara})\cdot P(\text{cara})\cdot P(\text{cara})\\[2ex]&=0,5\cdot 0,5\cdot 0,5\\[2ex]&=0,125\end{aligned}$

つまり、3回連続で表が出る確率は12.5%ということになります。

2 つの依存イベントの交差の確率

空の箱に青いボール 8 個、オレンジ色のボール 4 個、緑色のボール 2 個を入れます。最初に 1 つのボールを引き、次に引いた最初のボールをボックスに戻さずに別のボールを引いた場合、最初のボールが青で 2 番目のボールがオレンジになる確率はいくらですか?

この場合、2 回目の抽選でオレンジ色のボールを拾う確率は、最初の抽選で引いたボールの色に依存するため、イベントは依存します。したがって、問題が求める確率を計算するには、依存イベントの交差確率の公式を使用する必要があります。

$P(A\cap B)=P(A)\cdot P(B|A)$

最初の抽選で青いボールが得られる確率は簡単に決定できます。青いボールの数をボールの総数で割るだけです。

$P(\text{bola azul})=\cfrac{8}{8+4+2}=\cfrac{8}{14}=0,57$

一方、青いボールを受け取った後にオレンジ色のボールを引く確率は、オレンジ色のボールの数が異なり、さらにボックス内のボールが 1 つ少ないため、異なる方法で計算されます。

$P(\text{bola naranja}|\text{bola azul})=\cfrac{4}{7+4+2}=\cfrac{4}{13}=0,31$

したがって、最初に青いボールが描画され、次にオレンジ色のボールが描画される確率は、上記の 2 つの確率を乗算することによって計算されます。

$\begin{array}{l}P(\text{bola azul}\cap\text{bola naranja})=\\[2ex]=P(\text{bola azul})\cdot P(\text{bola naranja}|\text{bola azul})=\\[2ex]=0,57\cdot 0,31= \\[2ex]=0,18\end{array}$