Excel で二乗平均平方根誤差 (rmse) を計算する方法
統計学において、回帰分析は、予測変数 x と応答変数 y の関係を理解するために使用される手法です。
回帰分析を実行すると、予測変数の値に基づいて応答変数の予測値を示すモデルが得られます。
モデルが特定のデータセットにどの程度適合しているかを評価する 1 つの方法は、平均二乗誤差を計算することです。これは、予測値が観測値から平均してどの程度離れているかを示す指標です。
平均二乗誤差を求める公式は、一般的にRMSEとして知られており、次のとおりです。
RMSE = √[ Σ(P i – O i ) 2 / n ]
金:
- Σは「和」を意味する派手な記号です
- Piは、データセット内のi 番目の観測値の予測値です。
- O iは、データセット内のi 番目の観測値の観測値です。
- n はサンプルサイズです
技術的なメモ:
- 平均二乗誤差は、予測値を生成するあらゆるタイプのモデルに対して計算でき、その後、予測値をデータセットの観測値と比較できます。
- 平均二乗誤差は平均二乗偏差とも呼ばれ、RMSD と略されることがよくあります。
次に、Excel で平均二乗誤差を計算する方法の例を見てみましょう。
Excel で平均二乗誤差を計算する方法
Excel には RMSE を計算するための組み込み関数はありませんが、1 つの数式で非常に簡単に計算できます。 2 つの異なるシナリオの RMSE を計算する方法を示します。
シナリオ 1
シナリオでは、モデルからの予測値を含む 1 つの列と、観測値を含む別の列を含めることができます。以下の図は、このシナリオの例を示しています。
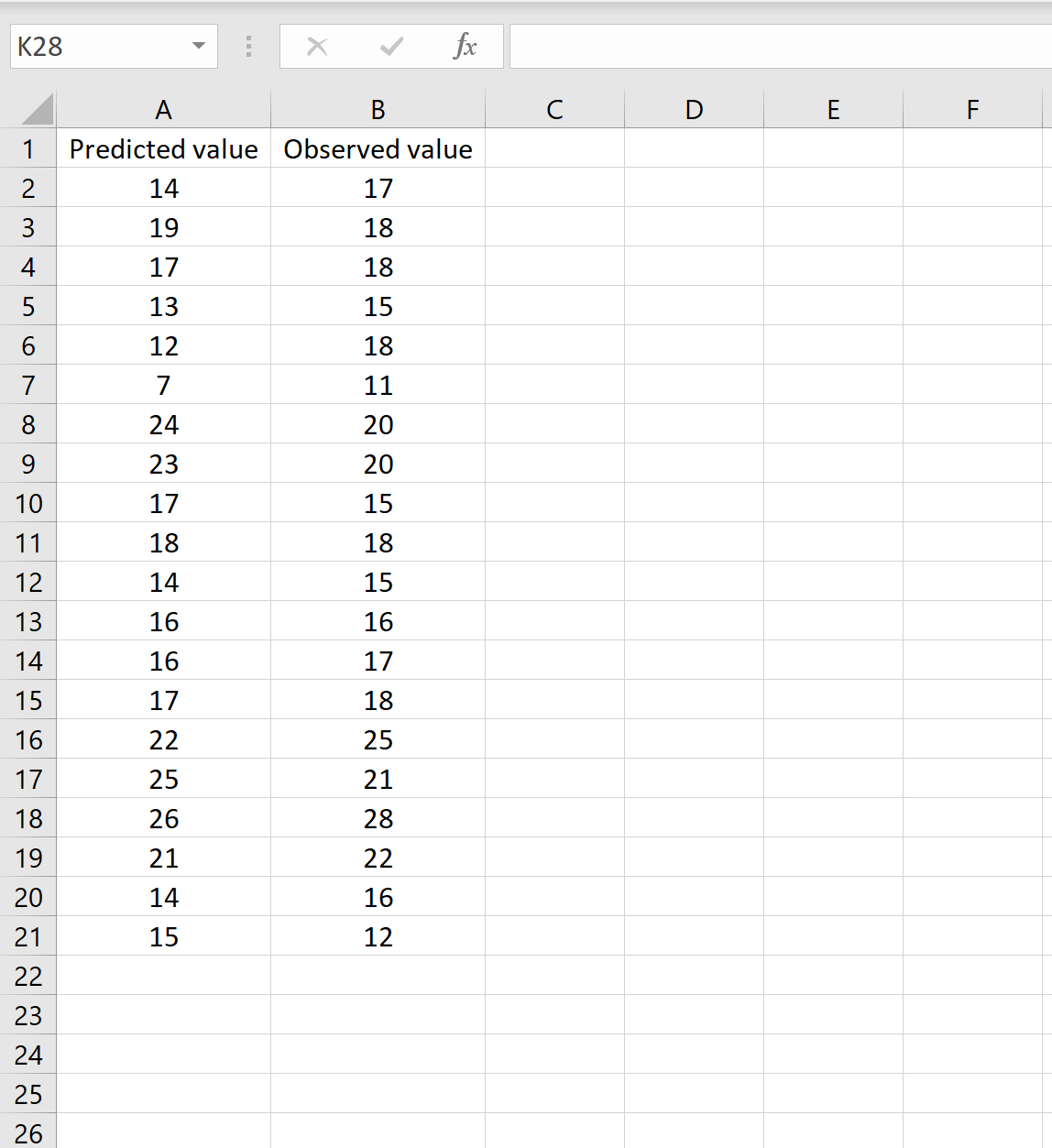
その場合は、任意のセルに次の数式を入力し、Ctrl + Shift + Enter をクリックすることで RMSE を計算できます。
=SQRT(SUMSQ(A2:A21-B2:B21) / COUNT(A2:A21))
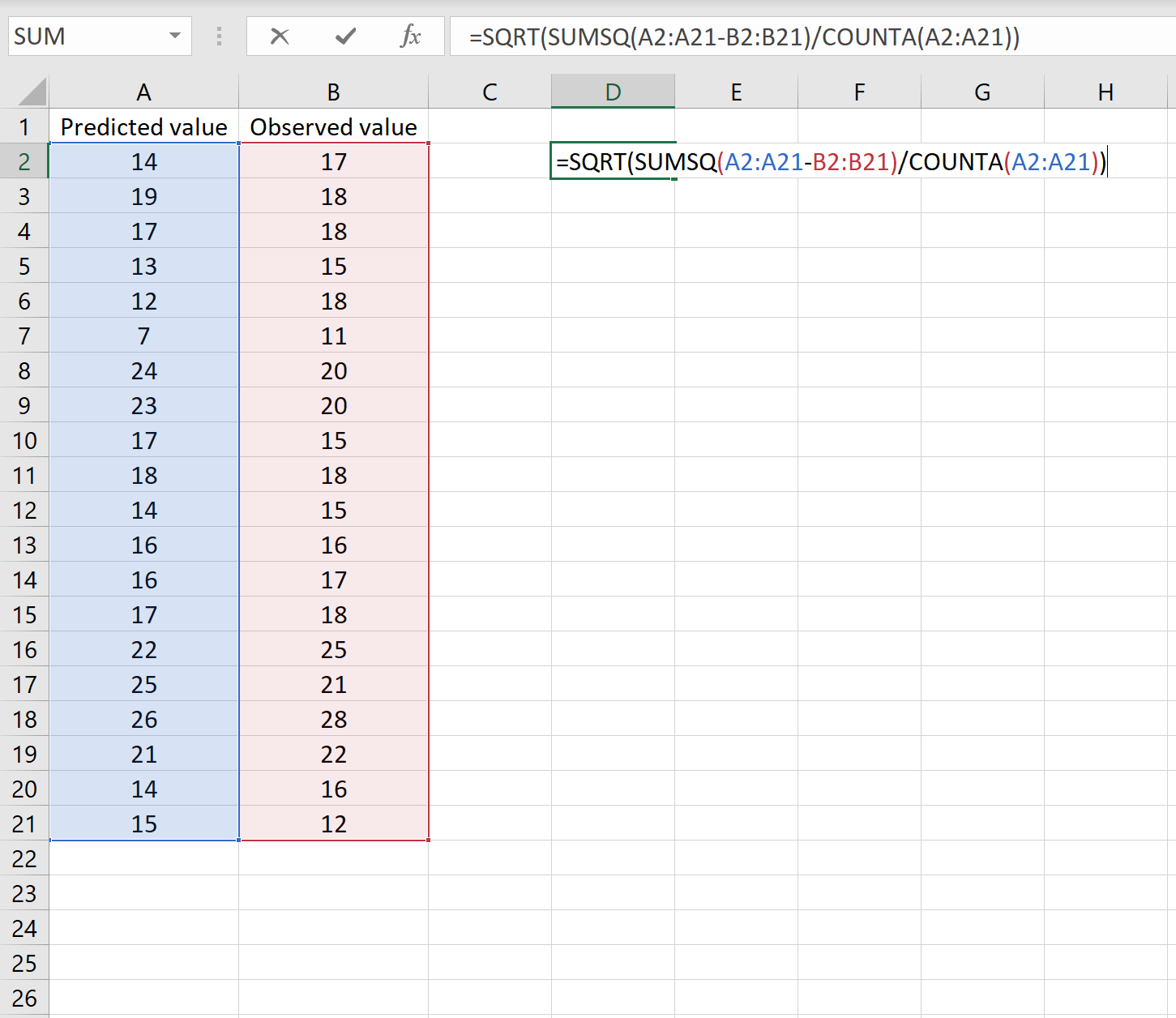
これは、平均二乗誤差が2.6646であることを示しています。
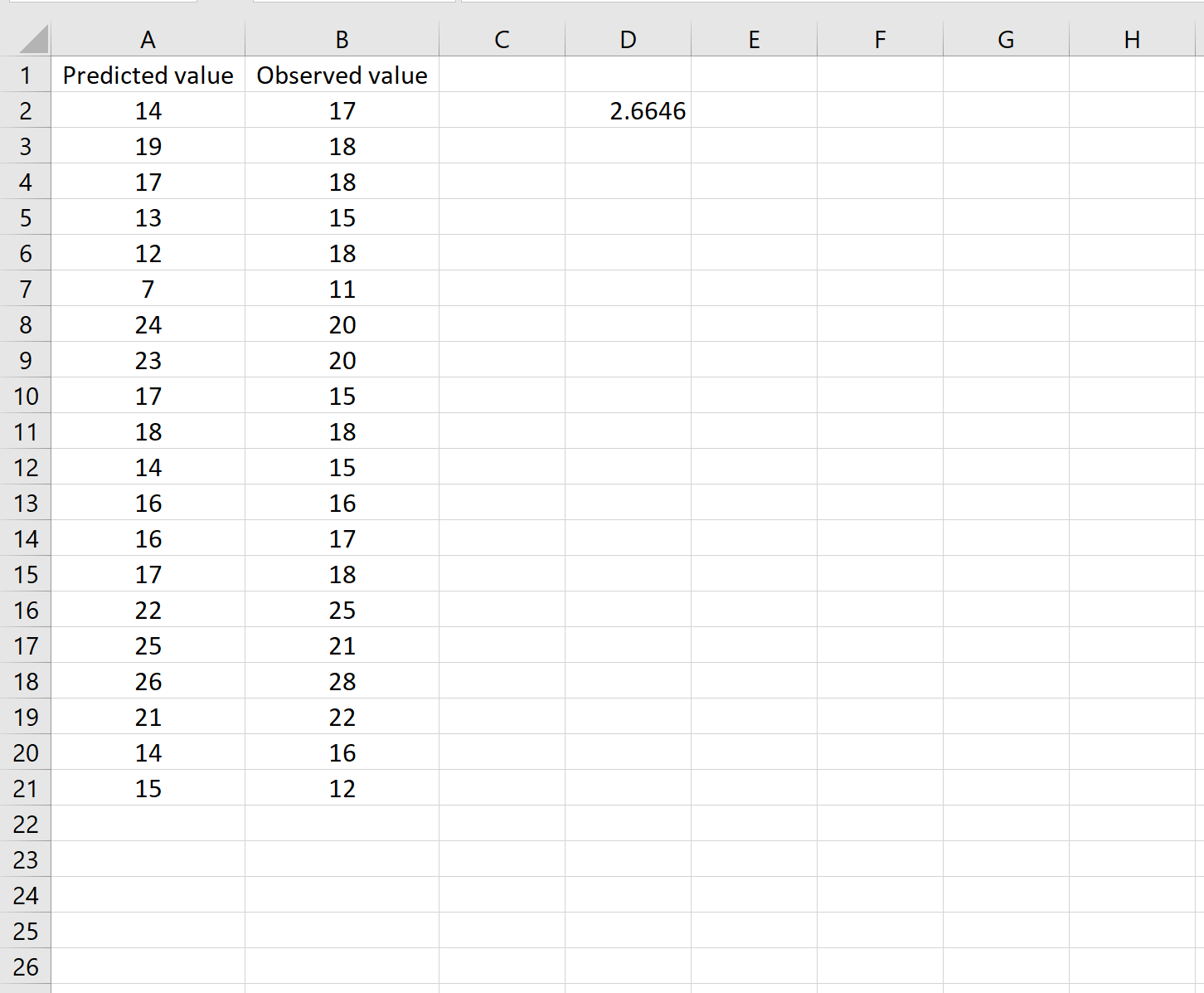
この式は少し難しく見えるかもしれませんが、分解してみると意味が分かります。
= SQRT( SUMSQ(A2:A21-B2:B21) / COUNT(A2:A21) )
- まず、 SUMSQ()関数を使用して、予測値と観測値の差の二乗和を計算します。
- 次に、範囲内の空ではないセルの数をカウントするCOUNTA()を使用して、データセットのサンプル サイズで除算します。
- 最後に、 SQRT()関数を使用して計算全体の平方根を求めます。
シナリオ 2
別のシナリオでは、予測値と観測値の差がすでに計算されている可能性があります。この場合、違いを示す列は 1 つだけになります。
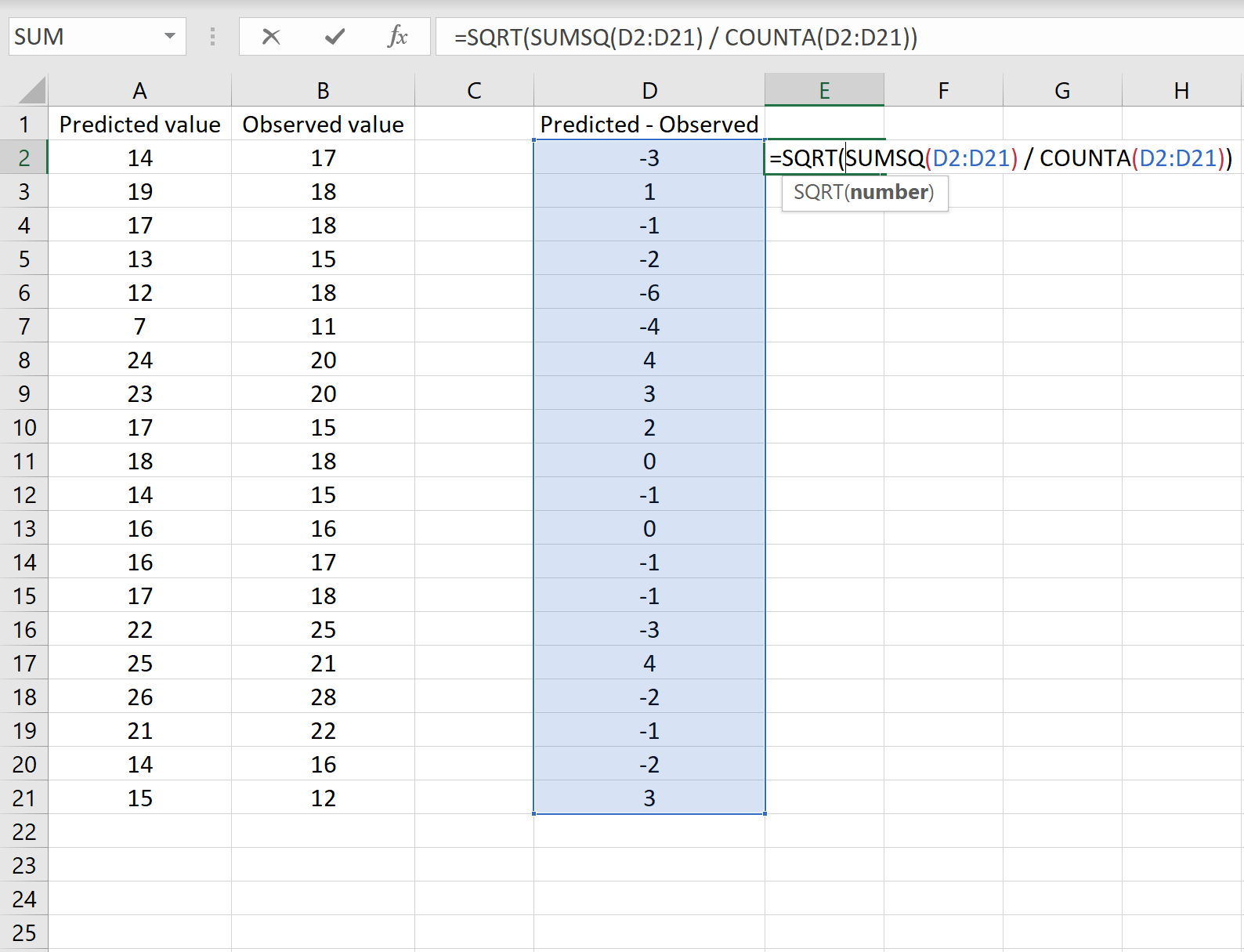
以下の図は、このシナリオの例を示しています。予測値は列 A に、観測値は列 B に、予測値と観測値の差は列 D に示されています。
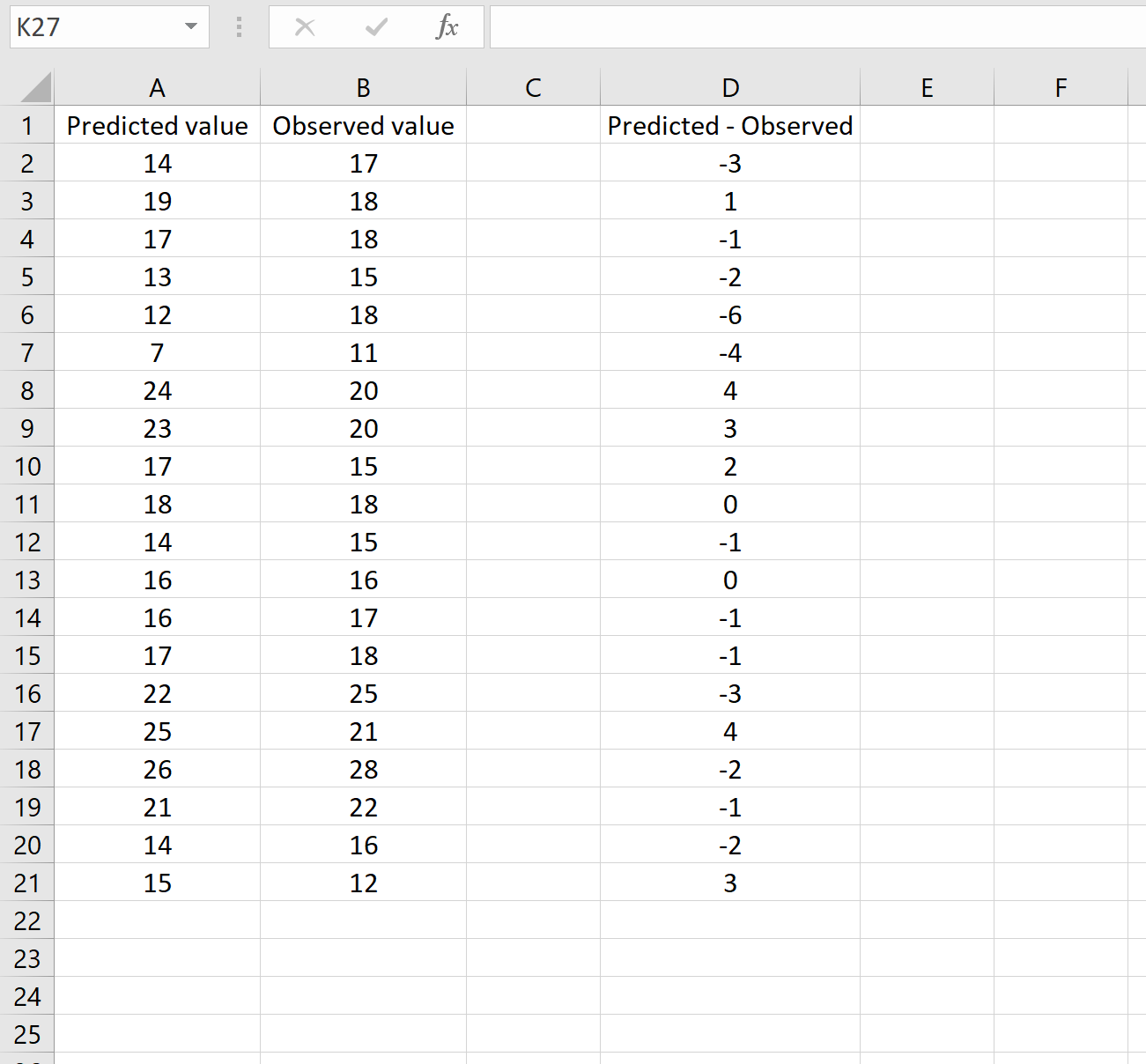
その場合は、任意のセルに次の数式を入力し、Ctrl + Shift + Enter をクリックすることで RMSE を計算できます。
=SQRT(SUMSQ(D2:D21) / COUNT(D2:D21))
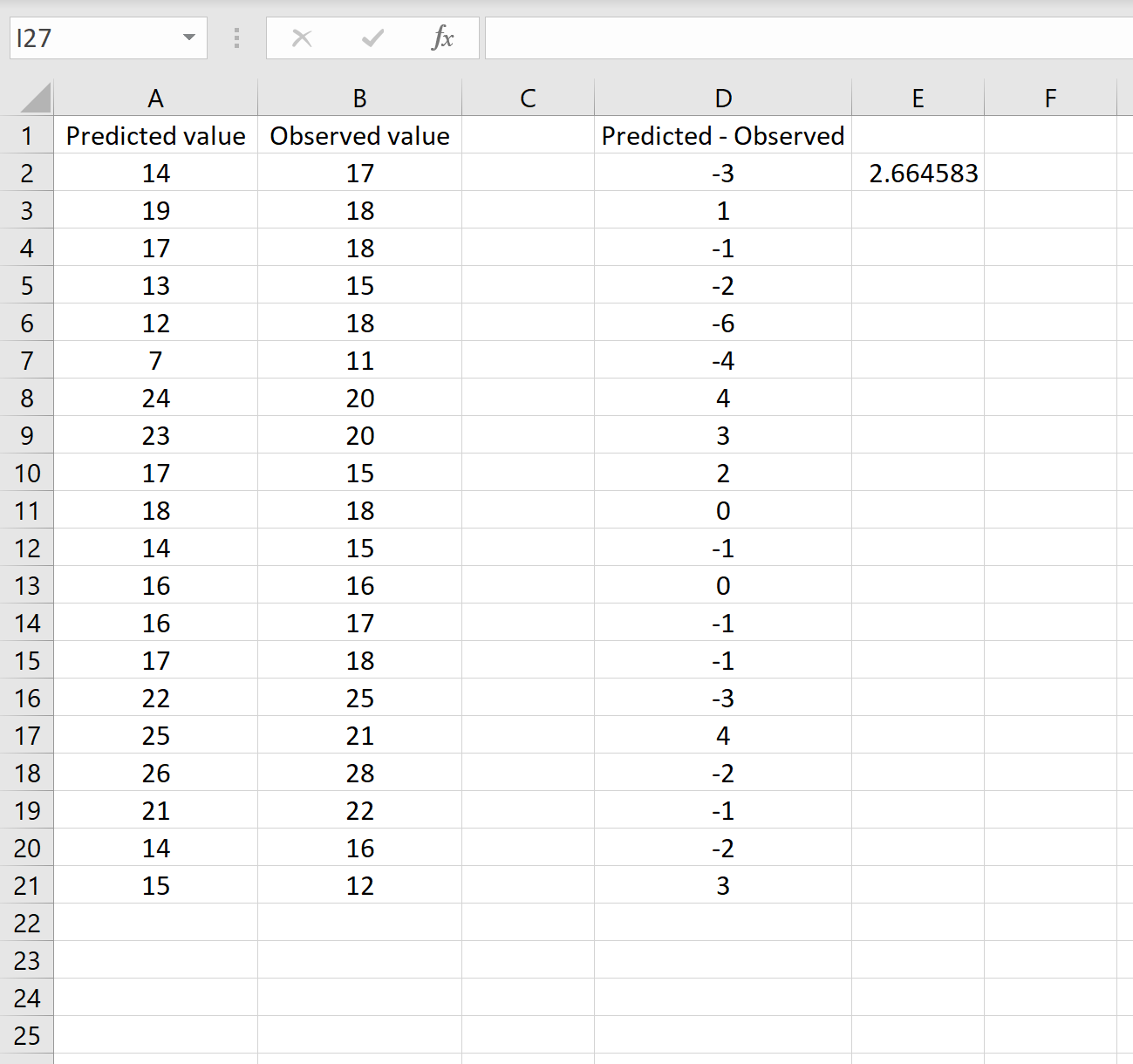
これは、平均二乗誤差が2.6646であることを示しており、これは最初のシナリオで得られた結果に対応します。これにより、RMSE を計算するためのこれら 2 つのアプローチが同等であることが確認されます。
このシナリオで使用した式は、前のシナリオで使用したものとわずかに異なります。
= SQRT( SUMSQ(D2:D21) / COUNT(D2:D21) )
- D 列の予測値と観測値の差はすでに計算済みなので、SUMSQ() 関数を使用して差の二乗の合計を計算できます。 D 列の値のみを含む関数。
- 次に、範囲内の空ではないセルの数をカウントするCOUNTA()を使用して、データセットのサンプル サイズで除算します。
- 最後に、 SQRT()関数を使用して計算全体の平方根を求めます。
RMSEの解釈方法
前述したように、 RMSE は、回帰モデル (または予測値を生成するモデル) がデータセットにどの程度「適合」できるかを確認する便利な方法です。
RMSE が大きいほど、予測値と観測値の差が大きくなり、回帰モデルのデータへの適合性が低下することを意味します。逆に、RMSE が小さいほど、モデルはデータにうまく適合できます。
2 つの異なるモデルの RMSE を比較して、どのモデルがデータに最も適合するかを確認することは特に便利です。
Excel のその他のチュートリアルについては、統計に関するすべての Excel チュートリアルをリストしたExcel ガイド ページを必ずご確認ください。