Stata で二次回帰を実行する方法
2 つの変数に線形関係がある場合、多くの場合、 単純な線形回帰を使用してそれらの関係を定量化できます。

ただし、2 つの変数に 2 次の関係がある場合は、 2 次回帰を使用してそれらの関係を定量化できます。

このチュートリアルでは、Stata で 2 次回帰を実行する方法を説明します。
例: Stata での二次回帰
労働時間と幸福度の関係を理解したいとします。 16 人の異なる人々の週の労働時間数と報告された幸福度 (0 から 100 のスケール) に関する次のデータがあります。
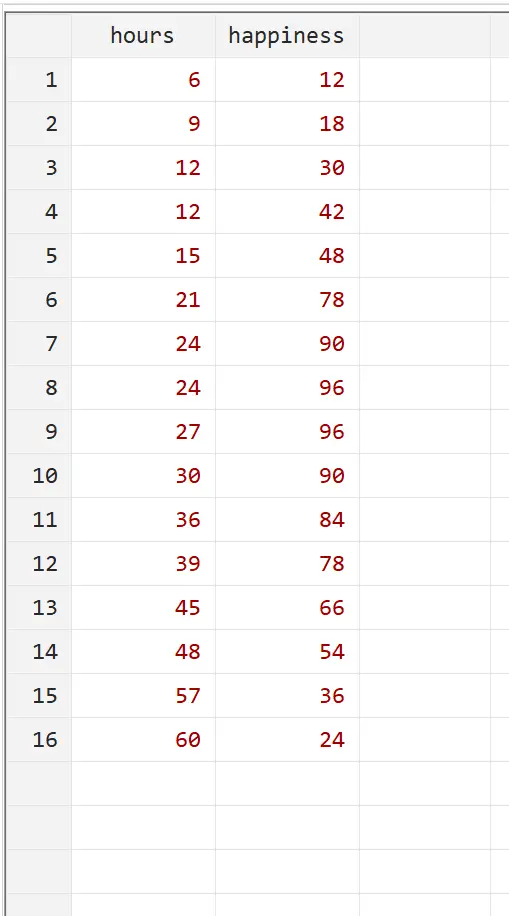
トップ メニューの[データ] > [データ エディター] > [データ エディター (編集)]を使用して、この正確なデータを Stata に入力することで、この例を再現できます。
Stata で 2 次回帰を実行するには、次の手順を使用します。
ステップ 1: データを視覚化します。
二次回帰を使用する前に、説明変数 (時間) と応答変数 (幸福度) の関係が実際に二次であることを確認する必要があります。コマンド ボックスに次のように入力して、散布図を使用してデータを視覚化しましょう。
幸せの時間を分散させる
これにより、次の散布図が生成されます。
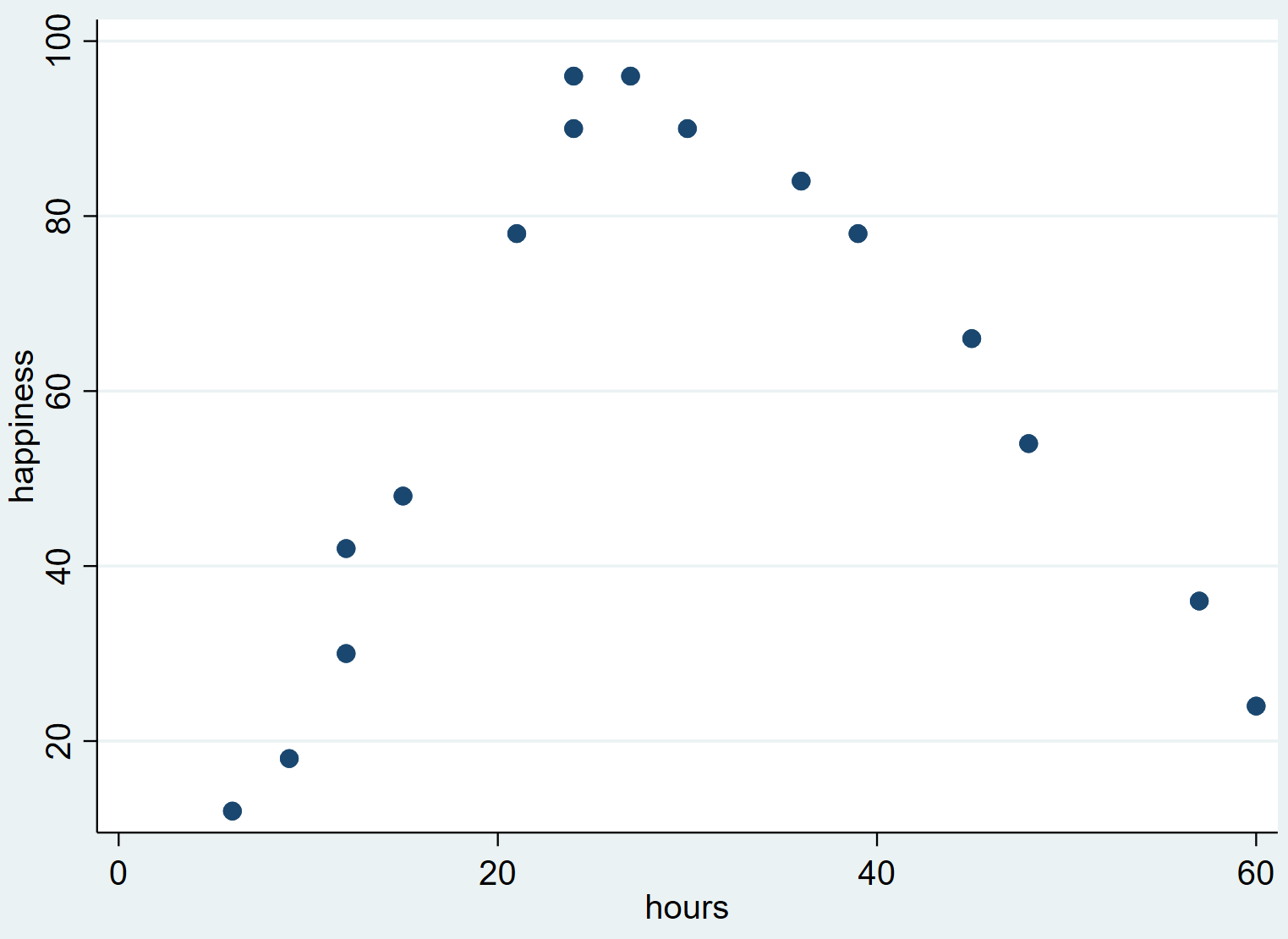
労働時間がゼロからある時点までは幸福度が増加する傾向にありますが、労働時間が約30時間を超えると幸福度は減少し始めることがわかります。
散布図のこの逆「U」字形は、労働時間と幸福度の間に 2 次の関係があることを示しています。つまり、この関係を定量化するには 2 次回帰を使用する必要があります。
ステップ 2: 二次回帰を実行します。
二次回帰モデルをデータに適合させる前に、時間予測変数の二乗値用の新しい変数を作成する必要があります。これを行うには、コマンド ボックスに次のように入力します。
gen hours2 = 時間*時間
この新しい変数を表示するには、トップ メニューから[データ] > [データ エディター] > [データ エディター (参照)]に移動します。
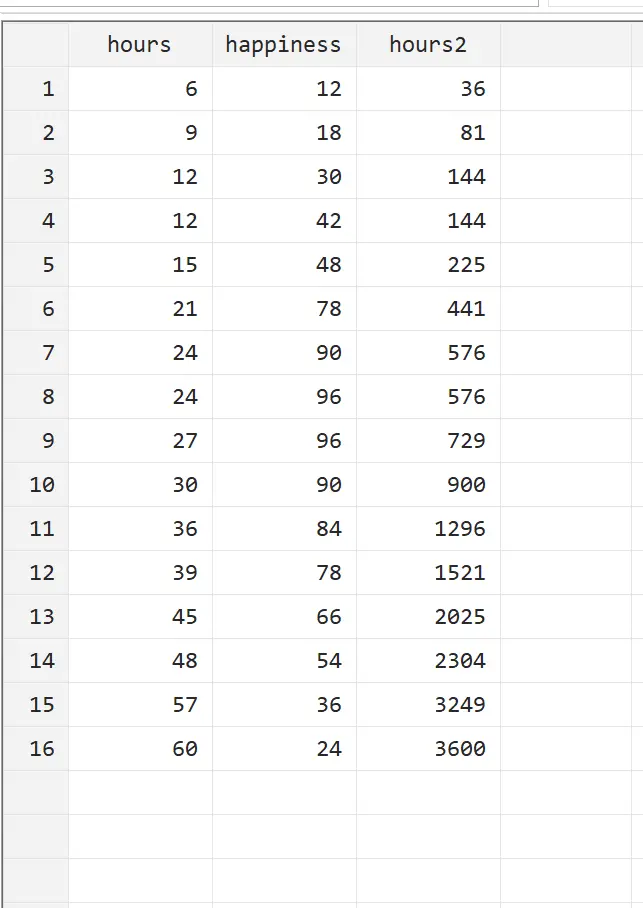
hours2 は単純に時間の 2 乗であることがわかります。これで、時間と時間 2 を説明変数として、幸福度を応答変数として使用して、二次回帰を実行できるようになりました。二次回帰を実行するには、コマンド ボックスに次のように入力します。
幸福時間の退行時間2
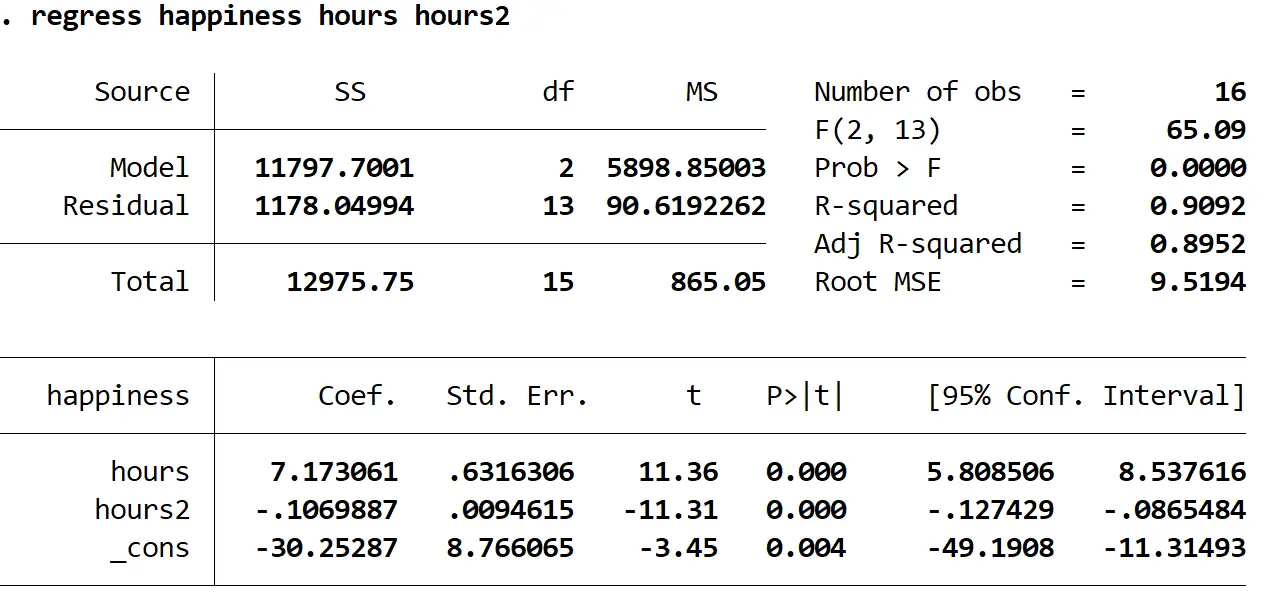
結果内の最も興味深い数値を解釈する方法は次のとおりです。
確率 > F: 0.000。これは全体的な回帰の p 値です。この値は 0.05 未満であるため、予測子変数hoursとhours 2の組み合わせが応答変数Happinessと統計的に有意な関係があることを意味します。
R二乗: 0.9092。これは、説明変数によって説明できる応答変数の分散の割合です。この例では、幸福度の変化の 90.92% は時間と時間で説明できます2 。
回帰式:出力テーブルに示されている係数値を使用して回帰式を作成できます。この場合、方程式は次のようになります。
予測される幸福度 = -30.25287 + 7.173061 (時間) – 0.1069887 ( 2時間)
この方程式を使用すると、週あたりの労働時間を考慮した個人の予測幸福度を見つけることができます。
たとえば、週に 60 時間働く人の幸福度は 14.97 になるはずです。
予測幸福度 = -30.25287 + 7.173061(60) – .1069887(60 2 ) = 14.97 。
逆に、週に 30 時間働く人の幸福度は 88.65 になるはずです。
予測幸福度 = -30.25287 + 7.173061(30) – .1069887(30 2 ) = 88.65 。
ステップ 3: 結果を報告します。
最後に、二次回帰の結果を報告します。これを行う方法の例を次に示します。
個人の労働時間とそれに対応する幸福度 (0 から 100 で測定) との関係を定量化するために、二次回帰が実行されました。分析には16人のサンプルが使用されました。
その結果、説明変数の時間と時間2と応答変数の幸福度の間に統計的に有意な関係があることがわかりました (F(2, 13) = 65.09、p < 0.0001)。
これら 2 つの説明変数を合わせて、説明される幸福度の変動の 90.92% を占めました。
回帰式は次のようになりました。
予測される幸福度 = -30.25287 + 7.173061 (時間) – 0.1069887 ( 2時間)