二項分布の概要

二項分布は、統計学で最もよく使われる分布の 1 つです。二項分布を理解するには、まず二項実験を理解することが役立ちます。

二項実験

二項実験は、次の特性を持つ実験です。

• 実験はn回繰り返される試行で構成されます。
• 各トライアルで考えられる結果は 2 つだけです。
• pで示される成功の確率は、各試行で同じです。
• 各テストは独立しています。

二項実験の最もわかりやすい例は、コイン投げです。たとえば、コインを10回投げたとします。次の 4 つの特性があるため、これは二項実験です。

• 実験はn回繰り返される試行で構成されます。試行は 10 回あります。
• 各トライアルには、表か裏かの 2 つの結果しかありません。
• pで示される成功の確率は、各試行で同じです。 「成功」を表の着地と定義すると、各試行の成功確率はちょうど 0.5 になります。
• 各トライアルは独立しています。あるコイントスの結果は、他のコイントスの結果に影響を与えません。

二項分布

二項分布は、 n回の二項実験でk回の成功が得られる確率を表します。

確率変数X が二項分布に従う場合、 X = kが成功する確率は次の式で求められます。

P(X=k) = _n C _k * p ^k * (1-p) ^nk

金：

• n:試行回数
• k:成功回数
• p:与えられた試行の成功確率
• _n C _k : n回の試行でk 個の成功を得る方法の数

たとえば、コインを3回投げたとします。上記の式を使用して、これら 3 回のトスで 0、1、2、および 3 の表が出る確率を決定できます。

P(X=0) = ₃ C ₀ * 0.5 ⁰ * (1-0.5) ^3-0 = 1 * 1 * (0.5) ³ = 0.125

P(X=1) = ₃ C ₁ * 0.5 ¹ * (1-0.5) ^3-1 = 3 * 0.5 * (0.5) ² = 0.375

P(X=2) = ₃ C ₂ * 0.5 ² * (1-0.5) ^3-2 = 3 * 0.25 * (0.5) ¹ = 0.375

P(X=3) = ₃ C ₃ * 0.5 ³ * (1-0.5) ^3-3 = 1 * 0.125 * (0.5) ⁰ = 0.125

注:各例_のnCkを計算するには、この組み合わせ計算機を使用しました。

単純なヒストグラムを作成して、この確率分布を視覚化できます。

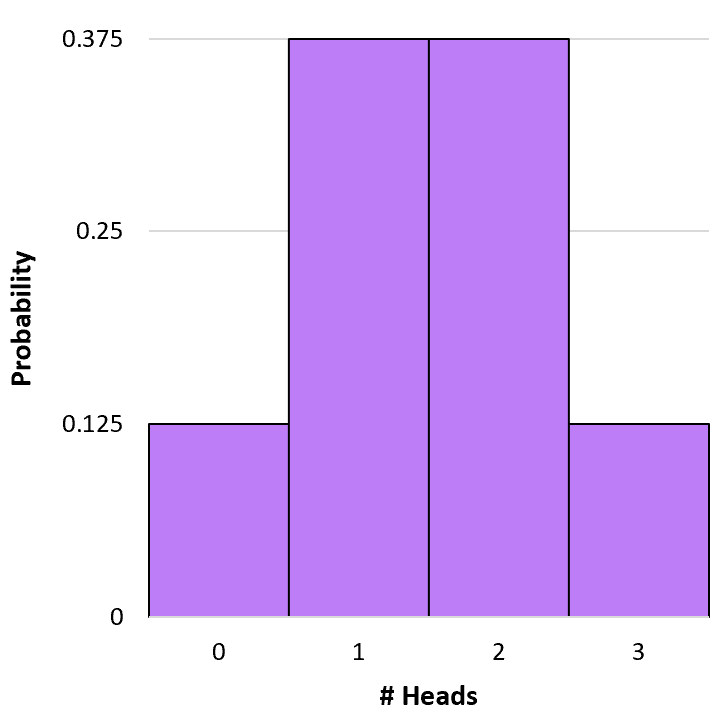
累積二項確率の計算

上記の式を使用して単一の二項確率 (たとえば、コインが 3 回投げて 1 回表になる確率) を計算するのは簡単ですが、累積的な二項確率を計算するには、個々の確率を加算する必要があります。

たとえば、コインを 3 回投げて表が出る確率を知りたいとします。この確率を計算するには次の式を使用します。

P(X≤1) = P(X=0) + P(X=1) = 0.125 + 0.375 = 0.5 。

複数の確率を加算する必要があるため、これは累積確率と呼ばれます。同様の式を使用して、結果ごとにk以下の表が得られる累積確率を計算できます。

P(X≤0) = P(X=0) = 0.125 。

P(X≤1) = P(X=0) + P(X=1) = 0.125 + 0.375 = 0.5 。

P(X≤2) = P(X=0) + P(X=1) + P(X=2) = 0.125 + 0.375 + 0.375 = 0.875 。

P(X≤3) = P(X=0) + P(X=1) + P(X=2) + P(X=3) = 0.125 + 0.375 + 0.375 + 0.125 = 1 。

ヒストグラムを作成して、この累積確率分布を視覚化できます。

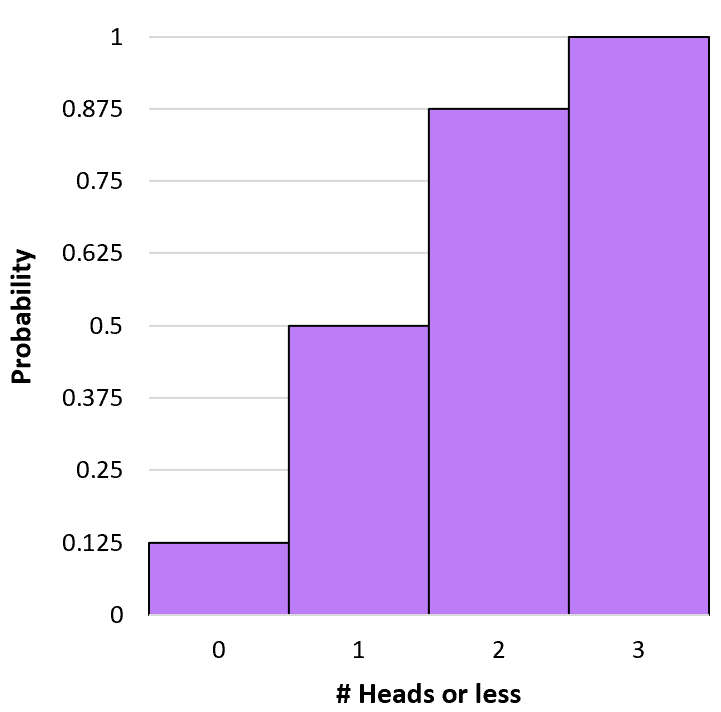
二項確率計算ツール

小さい数を扱う場合 (コインを 3 回投げるなど)、二項確率を手動で計算するのが合理的です。ただし、より大きな数 (例: 100 回の引き分け) を扱う場合、確率を手動で計算するのは困難な場合があります。このような場合、以下のような二項確率計算ツールを使用すると便利です。

たとえば、コインを n = 100 回投げるとします。与えられた試行で表が出る確率は p = 0.5 で、k = 43 回以下で表が出る確率を知りたいとします。

結果を解釈する方法は次のとおりです。

• コインがちょうど 43 回表になる確率は0.03007です。
• 43 回未満でコインの表が出る確率は0.06661です。
• コインが 43 回以下で表になる確率は0.09667です。
• コインが 43 回以上表になる確率は0.90333です。
• コインが 43 回以上表になる確率は0.93339です。

二項分布の性質

二項分布には次の特性があります。

分布の平均はμ = np

分布の分散はσ ² = np(1-p)です。

分布の標準偏差はσ = √ np(1-p)です。

たとえば、コインを 3 回投げたとします。 p = コインが表になる確率とします。

予想されるヘッドの平均数は μ = np = 3*.5 = 1.5です。

予想される人数の分散は σ ² = np(1-p) = 3*.5*(1-.5) = 0.75です。

二項分布の練習問題

次の練習問題を使用して、二項分布に関する知識をテストしてください。

問題 1

質問:ボブはフリースロー試投の 60% を成功させます。彼がフリースローを 12 回成功させた場合、ちょうど 10 回成功する確率はどれくらいですか?

回答:上記の二項分布計算ツールを p = 0.6、n = 12、k = 10 として使用すると、 P(X=10) = 0.06385であることがわかります。

問題 2

質問:ジェシカはコインを 5 回投げます。コインの表が 2 回以下になる確率はいくらですか?

回答: p = 0.5、n = 5、k = 2 で上記の二項分布計算ツールを使用すると、 P(X≤2) = 0.5であることがわかります。

問題 3

質問:特定の学生が特定の大学に合格する確率は 0.2 です。 10 人の学生が応募した場合、4 人以上が合格する確率はどれくらいですか?

回答: p = 0.2、n = 10、k = 4 で上記の二項分布計算ツールを使用すると、 P(X>4) = 0.03279であることがわかります。

問題4

質問:あなたはコインを 12 回投げます。予想される平均頭数はどれくらいですか?

回答:二項分布の平均は μ = np として計算されることを思い出してください。したがって、μ = 12*0.5 = 6 ヘッドになります。

問題5

質問:マークは試行回数の 10% でホームランを打っています。彼が特定の試合で 5 回の試行を打った場合、彼が打ったホームランの数の分散はいくらですか?

回答:二項分布の分散は σ ² = np(1-p) として計算されることを思い出してください。したがって、 ^σ2 = 6*.1*(1-.1) = 0.54 となります。

追加リソース

次の記事は、さまざまな統計ソフトウェアで二項分布を使用する方法を学習するのに役立ちます。

• Excel で二項確率を計算する方法
• TI-84 電卓で二項確率を計算する方法
• R で二項確率を計算する方法
• R で二項分布をプロットする方法