二項分布
この記事では、統計における二項分布とは何か、またそれが何に使用されるのかについて説明します。したがって、二項分布の定義、二項分布の例、およびこのタイプの確率分布の特性がわかります。さらに、オンライン計算機を使用して二項分布の確率を計算することもできます。
二項分布とは何ですか?
二項分布は、一定の成功確率で一連の独立した二分実験を実行した場合の成功数をカウントする確率分布です。
言い換えれば、二項分布は、一連のベルヌーイ試行の成功した結果の数を記述する分布です。
ベルヌーイ テストは、「成功」と「失敗」という 2 つの結果が考えられる実験であることに注意してください。したがって、「成功」の確率をpとすると、「失敗」の確率はq=1-pとなります。
一般に、実行される実験の総数はパラメーターnで定義され、 pは各実験の成功確率です。したがって、二項分布に従う確率変数は次のように記述されます。
![]()
二項分布では、まったく同じ実験がn回繰り返され、実験は互いに独立しているため、各実験の成功確率は同じ(p)であることに注意してください。
二項分布は、二項分布とも呼ばれます。
二項分布の例
二項分布の定義を理解したら、概念をよりよく理解するために、このタイプの分布に従う変数の例をいくつか見ていきます。
- コインを25回投げたときに表が出る回数。
- バスケットボール選手が同じ場所からバスケットに向かって60回シュートを打ったときのシュート数。
- サイコロを30回振って6の目が出た回数。
- 合計 50 人の受験者のうちの合格数。
- 100 製品のサンプル内の不良ユニットの数。
二項分布式
パラメーターx、n、p が与えられると、二項分布の確率関数は、 x倍p x倍(1-p) nxにおけるnの組み合わせ数として定義されます。
したがって、二項分布の確率を計算する式は次のようになります。

👉以下の計算機を使用して、二項分布に従う変数の確率を計算できます。
一方、二項分布の累積確率は、問題の成功事例の数の確率と以前のすべての確率を加算することによって計算されます。したがって、二項分布の累積確率を計算する式は次のようになります。
![Rendered by QuickLaTeX.com \displaystyle P[X\leq x]=\sum_{k=0}^x\begin{pmatrix}n\\k\end{pmatrix}p^k(1-p)^{n-k}](https://statorials.org/wp-content/ql-cache/quicklatex.com-e31ef4ae023b8bf51c0b6816bc787c91_l3.png)
二項分布に関する演習を解決しました
- コインを 10 回投げますが、6 つの表が出る確率はどれくらいですか?
すべての打ち上げは互いに独立しており、成功の確率も同じであるため、この問題の変数は二項分布に従います。
具体的には、2 つの可能な結果のうち 1 つだけが成功とみなされるため、成功の確率は 50% です。
![]()
したがって、この演習の分布は、合計 10 回の実験と確率 0.5 の二項分布になります。
![]()
したがって、6 つの表が得られる確率を決定するには、二項分布公式を適用する必要があります。
![Rendered by QuickLaTeX.com \begin{aligned}P[X=x]&=\begin{pmatrix}n\\x\end{pmatrix}p^x(1-p)^{n-x}\\[2ex]P[X=6]&=\begin{pmatrix}10\\6\end{pmatrix}0,5^6(1-0,5)^{10-6}\\[2ex]P[X=6]&=0,2051\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-17346d59c641378880b734dfe88210f6_l3.png)
したがって、コインを 10 回投げてちょうど 6 つの表が出る確率は 20.51% です。
二項分布の特徴
二項分布には次の特徴があります。
- 二項分布は 2 つのパラメータで定義されます。nはベルヌーイ実験の総数、 pは各ベルヌーイ実験の成功確率です。
![Rendered by QuickLaTeX.com \begin{array}{c}X\sim\text{Bin}(n,p)\\[2ex]n\geq 0\\[2ex]0\leq p\leq 1\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-cd9728a237a5f49107bf14f440620936_l3.png)
- 二項分布の平均は、実験の総数と各実験の成功確率の積に等しくなります。したがって、二項分布の平均を計算するには、 nにpを乗算する必要があります。
![]()
- 二項分布の分散は、試行の総数に成功の確率と失敗の確率を掛けたものに等しくなります。
![]()
- 二項分布の確率関数の式は次のとおりです。
![]()
- 同様に、二項分布の累積分布関数の式は次のとおりです。
![Rendered by QuickLaTeX.com \displaystyle P[X\leq x]=\sum_{k=0}^x\begin{pmatrix}n\\k\end{pmatrix}p^k(1-p)^{n-k}](https://statorials.org/wp-content/ql-cache/quicklatex.com-e31ef4ae023b8bf51c0b6816bc787c91_l3.png)
- 同じ確率を持つ 2 つの独立した二項分布の合計は、同じ確率値pを持つ二項分布と等価であり、 nは 2 つの分布の合計試行数の合計です。
![Rendered by QuickLaTeX.com \begin{array}{c}X\sim\text{Bin}(n,p)\qquad Y\sim\text{Bin}(m,p)\\[4ex]Z=X+Y \sim\text{Bin}(n+m,p)\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-dbc1a01b2d5654864d688cc46ac3a2e6_l3.png)
![]()
- ベルヌーイ分布は、 n=1 、つまり 1 回の実験のみが実行される二項分布の特殊なケースです。
![]()
- X 1 、 X 2 、…、X k が次のような独立した確率変数である場合、
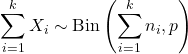
二項分布計算機
二項分布のパラメータp、n 、 xの値を次の計算機に入力して、確率を計算します。計算する確率を選択し、小数点区切りとしてドットを使用して数値を入力する必要があります (例: 0.1667)。