五分位数 (統計)

この記事では、五分位数とは何か、およびその計算方法について説明します。五分位を計算する解決済みの例がいくつかあり、さらに、オンライン計算機を使用して統計サンプルの五分位を計算することができます。

五分位数とは何ですか?

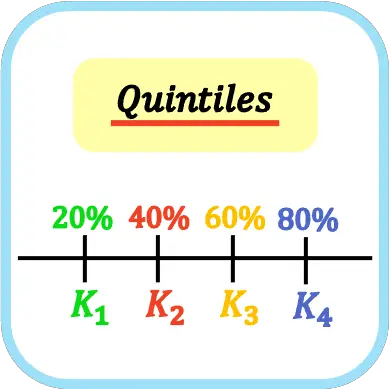
統計において、五分位とは、データセットを 5 つの等しい部分に分割する 4 つの値です。したがって、第 1、第 2、第 3、および第 4 の五分位は、それぞれサンプル データの 20%、40%、60%、および 80% を表します。

つまり、たとえば、第 3 五分位の値は、収集されたすべてのデータの 60% よりも高くなりますが、残りのデータよりは低くなります。

五分位の記号は、五分位インデックスが付いた大文字 K です。つまり、第 1 五分位は K ₁ 、第 2 五分位は K ₂ 、第 3 五分位は K ₃ 、第 4 五分位は K ₄です。ただし、文字 Q で表すこともできます (四分位数との混乱を招くため、お勧めしません)。

👉以下の計算機を使用して、任意のデータセットの五分位数を計算できます。

五分位数は、四分位数、十分位数、百分位数とともに非中心位置の尺度です。さらに興味がある場合は、Web サイトでこれらの分位タイプのそれぞれが何を意味するかを確認できます。

五分位には別の定義がある可能性があることに注意してください。経済学では、五分位数は所得順に並べた人口の割合を表します。言い換えれば、所得レベルによって人口をランク付けします。たとえば、第 1 五分位は人口の最も貧しい 20% に対応し、第 2 五分位は人口の最も所得が低い 40% に対応します。

五分位数の計算方法

サンプルまたは統計母集団の五分位の位置を計算するには、五分位の数にデータの総数に 1 を加えた合計を乗算し、その結果を 5 で割る必要があります。

したがって、五分位数の公式は次のようになります。

注意してください:この式の結果は、五分位の値ではなく、五分位の位置を示します。したがって、五分位は、式によって得られた位置にあるデータになります。

ただし、この式の結果が 10 進数になる場合があるため、結果が 10 進数であるかどうかに応じて 2 つのケースを区別する必要があります。

• 式の結果が小数部のない数値である場合、五分位は上記の式で指定された位置にあるデータです。
• 数式の結果が小数部を含む数値の場合、五分位値は次の式を使用して計算されます。

ここで、x _iおよびx _i+1は、最初の式で得られた数値が挟まれる位置の番号であり、 dは、最初の式で得られた数値の小数部分です。

データセットの五分位数を決定するための非常に多くの手順を見て怖くなったとしても、心配しないでください。実際には非常に簡単です。次の 2 つの例を読めば、よりよく理解できるでしょう。

注: 統計コミュニティでは、五分位の計算方法についてまだ完全に合意されていないため、少し異なる方法で説明されている本が見つかるかもしれません。

五分位数の計算例

データ系列から五分位を取得する方法について、段階的に解決する 2 つの演習を以下に示します。考えられる 2 つのケースがわかります。最初の演習では結果が 10 進数ではなく、2 番目の演習では結果が 10 進数になります。

例1

• 次のデータ系列の五分位数を計算します。

上の説明で見たように、五分位の位置を求める公式は次のとおりです。

パラメーターn はデータの総数 (49) を参照するため、最初の五分位の位置を見つけるには、 n を49 に、 k を1 に置き換える必要があります。

この式から数値 10 が得られました。これは、五分位が順序付きリストの 10 番目の位置にあり、データ 205 に対応することを意味します。

2 番目の五分位を計算するには、同じ式を使用する必要がありますが、 kを 2 に置き換えます。

したがって、2 番目の五分位は、順序付きリストの位置番号 20、つまり値 236 にあります。

もう一度、このプロセスを繰り返して五分位 3 を決定しますが、論理的にはk を3 に置き換えます。

したがって、第 3 五分位は位置 30 にあるデータであり、266 に対応します。

最後に、式を再度適用して、第 4 五分位を計算します。

したがって、第 4 五分位は 40 の位置にあるため、第 4 五分位は 286 になります。

例 2

• 次の表で収集された統計データの 4 つの五分位数を計算します。

前の例と同様に、五分位の位置を取得するには、次の式を使用する必要があります。

この場合、サンプル サイズは 42 の観測値であるため、最初の五分位の位置を見つけるには、パラメーターnを 42 に、 kを 1 に置き換える必要があります。

ただし、最初の例とは異なり、今回は式で 10 進数が得られるため、正確な五分位を計算するには次の式を適用する必要があります。

最初の式から得られる数値は 8.6 であるため、最初の五分位は 8 番目と 9 番目のデータの間にあり、それぞれ 78 と 79 になります。したがって、 x _iは 78、 x _i+1は 79、 dは得られた数値の小数部分、つまり 0.6 になります。

ここで、まったく同じ手順をもう一度実行して、2 番目の五分位を見つけます。まずその位置を計算します。

ただし、式から 17 と 18 の間の 10 進数が得られるため、第 2 五分位は 17 位と 18 位の間にあり、その値は順序付きリストの 109 と 112 にそれぞれ対応します。したがって、プロセスに 2 番目の式を適用して、正確な五分位値を決定します。

この方法を繰り返して 3 番目の五分位を取得し、最初にその位置を決定します。

計算された数値 25.8 は、五分位値が 25 番目と 26 番目の位置の間にあることを意味し、その値は 134 と 141 です。 したがって、正確な五分位値の計算は次のようになります。

最後に、同じ手順をもう一度繰り返して、五分位 4 を計算します。まず、その位置を見つけます。

したがって、第 4 五分位の正確な値は 34 ～ 35 の間となり、その位置はデータ 172 と 179 に対応します。 したがって、第 4 五分位の計算は次のようになります。

五分位計算機

次の計算機に統計データ セットを入力して、五分位を計算します。データはスペースで区切られ、小数点としてピリオドを使用して入力する必要があります。

グループ化されたデータの五分位数

データが間隔にグループ化されているときに五分位数を計算するには、まず次の式を使用してその間隔またはクラスを見つける必要があります。

したがって、五分位は、絶対頻度が前の式で得られた数よりもすぐに大きい区間内にあります。

五分位が属する区間がわかったら、次の公式を適用して五分位の正確な値を見つける必要があります。

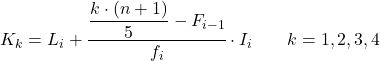
金：

• Ｌ _{ｉ は}、五分位が位置する間隔の下限である。
• nは観測値の総数です。
• F _i-1は、前の間隔の累積絶対頻度です。
• f _iは、五分位が位置する間隔の絶対周波数です。
• I _iは五分位間隔の幅です。

これがどのように行われるかがわかるように、間隔にグループ化された次のデータ系列の五分位を計算する解決された例を次に示します。

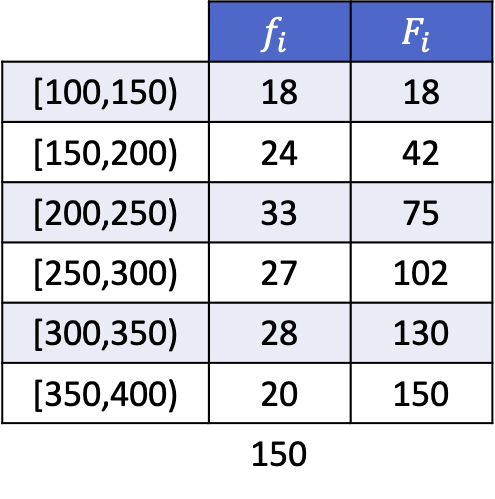
データはグループ化されているため、次の方法を使用して五分位を計算する必要があります。まず、五分位が該当する範囲を決定し、次に五分位の正確な値を見つけます。

したがって、最初の五分位が位置する間隔を見つけるには、次の式を使用します。

最初の五分位は、累積絶対頻度が 30.2 よりすぐ大きい区間にあります。この場合、それは累積絶対頻度が 42 である区間 [150,200) です。そして、五分位区間がわかったら、次の 2 番目の式を適用します。正確な値を決定するプロセス:

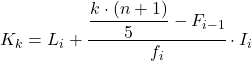
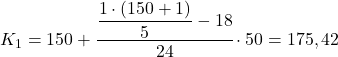
次に、同じ手順を繰り返して 2 番目の五分位を取得し、最初にそれが存在する間隔を計算します。

60.4 のすぐ上の累積絶対頻度は 75 であるため、第 2 五分位範囲は [200 250) です。したがって、対応する値を 2 番目の式に代入して、正確な五分位値を計算します。

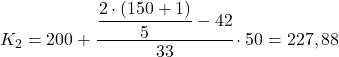
同じ手順を 3 回実行して、五分位 3 を取得します。まず、五分位が位置する間隔を決定します。

その累積絶対頻度 (102) が 90.6 のすぐ上の値であるため、五分位は区間 [250,300) にあります。したがって、第 3 五分位の正確な値の計算は次のようになります。

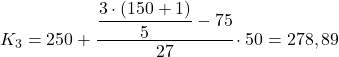
最後に、4 番目の五分位を見つけます。いつものように、最初にその間隔を見つけます。

絶対頻度が 120.8 よりすぐ大きい区間は [300.350) で、その値は 130 です。したがって、第 4 五分位の正確な値は次のようになります。