人口の意味
この記事では、統計における人口の意味について説明します。同様に、母集団の平均値の公式は何か、母集団の平均値の信頼区間はどのように計算されるのか、さらには母集団の平均値と「標本」の平均値の差は何かもわかります。
母集団の平均はいくらですか?
母集団の平均は、統計母集団のすべての要素の算術平均です。したがって、母集団の平均を計算するには、すべての母集団の値を加算し、母集団内の要素の合計数で割る必要があります。
母集団平均の記号はギリシャ文字のμです。
同様に、母集団平均は母集団を表す変数の期待値としても定義できます。
母集団平均の計算方法
母集団平均の定義を理解したら、その意味をより深く理解するために母平均がどのように計算されるかを見てみましょう。
統計母集団のすべての値がわかっている場合は、単純に算術平均の公式を適用して母集団の平均を計算する必要があります。したがって、この場合、母集団の平均を計算するには、すべての母集団の値を合計し、データの総数で割る必要があります。
したがって、母集団のすべての要素の値がわかっている場合、母集団の平均を計算する式は次のようになります。
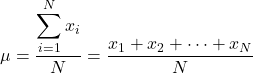
ただし、一般にすべての母集団の値がわかっているわけではないため、通常は母集団の平均値は区間によって推定されます。
母集団平均の信頼区間
実際には、母集団内のすべての個人を研究することは不可能であるため、通常は母集団のランダムなサンプルが選択され、その値に基づいて母集団の平均値の近似が行われます。より正確には、母集団全体の平均が存在する可能性が非常に高い区間を計算します。この区間は母平均の信頼区間と呼ばれます。
母集団平均の信頼区間は、Z α/2の値に標準偏差 (σ) を掛け、サンプルの高さ (n) の平方根で割った値をサンプル平均に加算および減算することによって計算されます。したがって、母集団平均の信頼区間を計算する式は次のようになります。
![]()
上記の式は、母集団の分散がわかっている場合に使用されます。ただし、母集団の分散が不明な場合 (最も一般的なケース)、平均の信頼区間は次の式を使用して計算されます。
![]()
金:
-

はサンプル平均です。
-

は、確率 α/2 の n-1 自由度のスチューデント t 分布の値です。サンプルサイズが大きく、95% の信頼水準の場合は通常 1.96 に近く、99% の信頼水準の場合は通常 2.576 に近くなります。
-

は標本標準偏差です。
-

はサンプルサイズです。
母集団平均とサンプル平均
最後に、要約として、これら 2 つの統計概念を明確にするために、母集団の平均とサンプルの平均の違いを確認します。
母集団の平均とサンプルの平均の差は、平均が計算される値の範囲です。母平均は統計上の母集団全体の平均ですが、サンプル平均は母集団のサンプルの平均です。
さらに、母集団の平均値と標本平均値を区別するために、それらは異なる記号で表されます。母集団平均の記号は次のとおりです。
![]()
一方、標本平均の記号は次のようになります。
![]()
。
![Rendered by QuickLaTeX.com \begin{array}{c}\mu =\text{Media poblacional}\\[2ex]\overline{x} = \text{Media muestral}\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-f812349b186d7c1a8abdd1d2807f0a60_l3.png)
これら 2 種類の平均の違いについてまだ疑問がある場合、またはサンプル平均の計算について詳しく知りたい場合は、次の記事を参照してください。